Teoria dei residui

1) Residuo :

Si tratta del coefficiente a_-1 della serie di Laurent    

 

2) Formula per calcolare il residuo in z = a quando a è un polo semplice :

Si ottiene a partire dallo sviluppo in serie di Laurent, moltiplicando per (z-a) e facendo il limite si annullano tutti i termini ad eccezione del coefficiente c_-1 .

 

3) Formula per calcolare il residuo in z = a quando a è un polo semplice ed f(z) è un rapporto di funzioni :

La f(z) ha un polo ossia il denominatore ha uno zero in a e quindi si può scrivere in serie di Taylor  ed osservando la funzione si trova che il coefficiente di  è proprio

 

4) Formula per calcolare il residuo in z = a quando a è un polo di ordine m :

Se a è un polo di ordine m allora la serie di Laurent di f(z) è :     moltiplicando per  (z-a)^m si ottiene una serie di Taylor derivando la quale m-1 volte e facendo il limite per z®a si ottiene a_-1 infatti  da cui la formula richiesta.

 

5) Teorema dei residui :

Sia f(z) una funzione ad un sol valore ed analitica all´interno e sulla linea semplice chiusa C eccezion fatta per le singolarità a, b, c,... all´interno di C che hanno residui dati da a_-1 , b_-1 , c_-1 ,.... Þ 

È sufficiente prendere per ogni singolarità una circonferenza contenuta in C e centrata nella singolarità stessa, ed osservare che      ed osservare che ognuno degli integrali a secondo membro si può semplicemente estrapolare dal coefficiente a_-1 della serie di Laurent, infatti si ha .

 

6) Residuo all´infinito :

Il residuo della funzione analitica f(z) nel punto z = ¥ è il complesso uguale al valore della integrale

 

7)       Se f(z) è una funzione analitica in tutto il piano complesso ad eccezione di un numero finito di punti singolari isolati tra i quali z = ¥    Þ  la somma dei residui è zero.

8) Lemma di Jordan :

Se la funzione f(z) è analitica in tutto il semipiano superiore ad eccezione di un numero finito di punti singolari isolati e tende a zero per |z| ® ¥   uniformemente rispetto a  q   con W  0 £ q  £ p   Þ    per  a > 0  si ha  essendo Cr´ la arco di circonferenza del semipiano superiore con |z| = R .

Si ha  da cui ponendo |f(x)| < m_R    x = Re^{i j}    e   dx = i Re^{i j} dj   si ha 

 e sfruttando che in [0,p/2] senj > 2j/p si ha :    e quindi il lemma è dimostrato.

 

9) Se f(x) è una funzione definita su tutto la asse reale e può essere prolungata analiticamente al semipiano superiore ed in tale semipiano soddisfi il Lemma di Jordan e non abbia punti singolari sulla asse reale Þ $  essendo z_k   i punti singolari della funzione f(z) nel semipiano superiore.

 

10)Derivata logaritmica :

Se f(z) è una funzione analitica univoca con un numero finito di punti di singolarità isolati, tutti poli nessuno dei quali si trova sulla frontiera del dominio allora la funzione ausiliaria  è detta derivata logaritmica

 

11) Residuo logaritmico :

Si tratta dei residui della funzione ausiliaria j(z) calcolati nei suoi punti di singolarità.

 

12) Valore del residuo logaritmico in uno zero di ordine k della funzione f(z) :

Il residuo logaritmico è pari all´ordine dello zero.

Si dimostra osservando che se a è uno zero di ordine n per f(z) allora in un suo intorno si può scrivere f(z) = (z-a)ⁿ f₁(z)

quest´ultima viene utilizzata nel calcolo della funzione ausiliaria 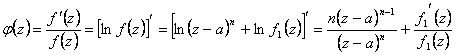 semplificando e ricordando che il residuo è pari al coefficiente di (z-a)^-1 si ottiene che esso vale n ossia è pari alla molteplicità dello zero.

 

13) Valore del residuo logaritmico in un polo di ordine k della funzione f(z) :

Il residuo logaritmico è pari all´ordine del polo preso con il segno negativo.

Si dimostra osservando che se a è un polo di ordine n per f(z) allora in un suo intorno si può scrivere f(z) = (z-a)^-p f₁(z)

quest´ultima viene utilizzata nel calcolo della funzione ausiliaria 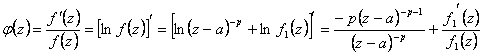 semplificando e ricordando che il residuo è pari al coefficiente di (z-a)^-1 si ottiene che esso vale -p ossia è pari alla molteplicità del polo cambiata di segno.

 

14) Teorema della argomento :

Se f(z) è una funzione analitica ovunque in un dominio chiuso G eccetto che in un numero finito di punti singolari z_k situati all´interno di G. Supponiamo che tutti gli z_k siano dei poli e che la funzione f(z) non si annulli in nessun punto della frontiera G del dominio G                                 Þ                           la differenza tra il numero totale degli zeri N ed il numero totale dei poli P della funzione f(z) del dominio G è definita dall´espressione .

Il teorema si dimostra calcolando l´integrale al secondo membro tramite il teorema dei residui ed osservando che il residuo logaritmo di una funzione in uno zero è proprio pari alla molteplicità dello 0 ed analogamente il residuo logaritmico in un polo è proprio pari alla molteplicità algebrica del polo stesso.

 

15) Interpretazione geometrica del teorema della argomento :

Si deve sostituire all´interno della integrale del teorema della argomento       e scomporre il logaritmo come logaritmo del modulo più i volte la variazione della argomento della funzione, si ha  

Infatti   è una funzione reale univoca quindi la variazione del suo argomento è 0 mentre il 2° membro esprime la variazione della argomento ossia il numero di giri totali attorno al punto w=0 che il punto w compie quando il punto z percorre il bordo del dominio nel senso positivo.

 

16) Indice di un punto rispetto ad una curva :

L´indice di un punto rispetto ad una curva chiusa è il numero di volte che questa viene percorsa rispetto al punto.

 

17) Teorema di Rouche :

Se le funzioni f(z) e j(z) sono analitiche nel dominio chiuso G, e sulla frontiera G del dominio G vale la disuguaglianza |f(z)|_G > |j(z)|_G      Þ                il numero totale di zeri della funzione F(z) = f(z) + j(z) è uguale al numero totale di zeri della funzione f(z).

Si ha che il numero di zeri della funzione F(z) è  mentre per la funzione f(z) il numero di zeri è   sottraendo membro a membro dobbiamo trovare che la differenza tra il numero degli zeri deve essere nulla. Si ha 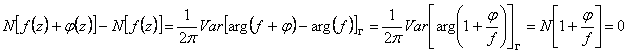 infatti il punto w = 0 si trova esternamente al circuito percorso da w.

 

18) Teorema fondamentale della algebra :

Un polinomio di grado n possiede nel piano complesso esattamente n zeri (contando anche la loro molteplicità) .

Ci si riporta in condizione di poter applicare il teorema di Rouche Capelli a tal fine se si prende   e   , scrivendo il rapporto dei moduli si ha   , si osserva che si può sempre trovare una circonferenza di raggio R tale che    e quindi si ha |g(z)| < |f(z)|  pertanto per il teorema di Rouche il polinomio f(z) + g(z) possiede lo stesso numero di zeri del polinomio f(z) il quale ha n zeri tutti nell´origine.