Teoremi sulle serie di Fourier
1) Teorema di Eulero sulla determinazione dei coefficienti della serie di Fourier :
I coefficienti della serie di Fourier sono determinati dai 2 seguenti integrali :
Dal polinomio di Fourier 
moltiplicando per cosmx (m = 0,1,...,n) ed integrando tra -p e p si ha 
. Analogamente moltiplicando per senmx (m = 0,1,...,n) ed integrando tra -p e p si ha 
. Avendo sfruttato i seguenti integrali notevoli :
; 
; 
2) Identità di Pitagora Parseval :
Se la funzione f(x) soddisfa la condizione di Dirichlet ed an e bn sono i coefficienti della serie di Fourier Þ
Si dimostra prendendo il polinomio trigonometrico, 
moltiplicandolo per f(x) ed integrando tra -p e p si ottiene : 
avendo sfruttato gli integrali 
, 
e 
.
3) Teorema sulla convergenza in media quadratica :
Al variare di sn tra tutti i polinomi trigonometrici di grado n, lo scarto quadratico medio 
risulta minimo se sn = sn dove sn è la somma parziale n-esima della serie di Fourier associata ad f.
Quadrando si ottiene
e sostituendo
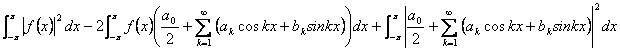
per il 1° termine si può sfruttare l´identità di Parseval mentre per il 2° termine si prende il polinomio trigonometrico, lo si moltiplica per 2f(x) e si integra tra -p e p. Ne risulta la tesi.
4) Disuguaglianza di Bessel :
Si ricava dalla convergenza in media quadratica osservando che 
in quanto la funzione integranda è positiva , pertanto il risultato trovato in quel caso è valido come disuguaglianza.
5) Teorema sulla convergenza puntuale :
Se f è una funzione continua a tratti e periodica con periodo 2p
Þ La serie di Fourier della f converge in ogni punto x nel quale è soddisfatta la condizione di Dirichlet e la sua somma in tale punto vale 
mentre se x è un punto di continuità per f allora la serie converge con somma f(x). Essendo f(x-) = il valore del limite sinistro e f(x+) = il valore del limite destro.
6) Teorema sulla convergenza uniforme :
Se f è una funzione continua e con derivata continua eccetto al più un n° finito di punti nei quali è comunque rispettata la condizione n° 2 di Dirichlet Þ La serie di Fourier della f converge assolutamente ed uniformemente in Â.