Teoremi sulla integrazione multipla
1) Sia A un insieme limitato Þ
A è misurabile Û la sua frontiera è misurabile ed ha misura 0
2) Se ho una funzione continua su di un compatto misurabile T Þ
il suo grafico è un insieme limitato e misurabile ed ha misura nulla.
La funzione è continua su di un compatto quindi per Heine - Cantor è anche uniformemente continua il che implica che se prendo w´ e w´´ Î T tali che || w´ - w´´ || < d allora si ha che || f(w´) - f(w´´) || < e.
Si effettua una decomposizione regolare (di diametro < d) di un rettangolo il quale contenga il dominio T.
Per Bolzano Weierstrass (Se E Í Ân è un insieme chiuso e limitato Þ esistono Max(E) e Min(E) )
su ognuno dei Ti esisterà il massimo ed il minimo della funzione, e si crea un intervallo di Â3 con altezza compresa tra il minimo ed il massimo assunto dalla funzione sull´ intervallino. Pertanto la misura della superficie è data dalla somma delle misure di questi intervalli di Â3 ossia 
< e in quanto la funzione è continua su di un compatto quindi per Heine - Cantor è anche uniformemente continua il che implica che se prendo w´ e w´´ Î T tali che || w´ - w´´ || < d allora si ha che || f(w´) - f(w´´) || < e.
3) Il cilindroide è un insieme misurabile :
Basta dimostrare che la sua frontiera ha misura tridimensionale nulla così è infatti in alto per la f(x,y) per il teorema precedente e così è per la base in quanto ha altezza 0 come pure per la parete laterale, entrambe infatti possono essere racchiuse in un plurirettangolo di Â3 di misura infinitesima.
4) Se ho una funzione costante L su di un compatto misurabile di base TÎÂ2 e quindi D è il cilindroide di base T, si ha :
Si supponga che la base sia contenuta nel plurintervallo P2 e contenga il plurintervallo P1 cioè P1 Ì T Ì P2 quindi si ha m(P1) < m(T) < m(P2) , del resto L è costante quindi Lm(P1) < Lm(T) < Lm(P2) con Lm(T) = m(D) si ha quindi
|m(D) - Lm(t)| < L |m(P2) -m(P1)| £ L e in quanto per il teorema di Heine Cantor se f è continua su di un compatto allora f è uniformemente continua e quindi se la distanza tra i due punti del dominio è < d Þla distanza tra le immagini è minore di e .
5) Se ho una funzione continua su di un compatto misurabile TÎÂ2 e quindi D è il cilindroide di base T, si ha :
Per il teorema di Heine Cantor essendo la funzione continua su di un compatto è anche uniformemente continua pertanto scegliendo una ampiezza minore di d per la decomposizione regolare del dominio T otterremo una distanza tra le immagini minore di e .
a) sA,p = 
è compresa tra la somma di Cauchy che utilizza il minimo della funzione su ogni piastrella della decomposizione regolare e la misura di Cauchy che invece impiega il massimo.
b) La misura del cilindroide S m(Di) è compresa tra la misura del cilindroide che utilizza il massimo valore della f su ogni piastrella e la misura del cilindroide che utilizza il minimo valore della f su ogni piastrella.
Da a) e b) dato che la differenza tra massimo e minimo è su ogni piastrella minore di e allora si ha che | sA,p - l | < e infatti 
6) Formula di riduzione per integrali doppi :
Se f è continua su di un dominio T semplice rispetto alla asse x Þ 
Sola interpretazione geometrica
7) Formula di riduzione per integrali tripli mediante integrazione per fili :
Se f è continua su di un dominio T semplice rispetto al piano xy Þ 
Sola interpretazione geometrica
8) Formula di riduzione per integrali tripli mediante integrazione per sezioni :
Se si ha a < x < b e le sezioni di D con un piano ortogonale alla asse x sono misurabili allora si ha :
Sola interpretazione geometrica
9) Formula per il cambiamento di variabili :
Se A è un compatto misurabile avente come immagine T ed r(u,v) è una biiezione il cui jacobiano è non nullo Þ
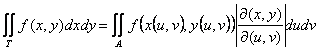
Sola interpretazione geometrica
10) Teorema di Pappo Guldino :
Il volume del solido S che si ottiene da una rotazione completa intorno alla asse z di un insieme T limitato e misurabile contenuto nel piano x = 0 è dato dalla formula 
essendo 
la coordinata del centroide.
Si ottiene passando in coordinate polari e ricordando la definizione di baricentro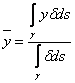 
.