Teoremi sugli integrali

1) Se f è una funzione limitata e D₁ e D₂ sono 2 suddivisioni di [a,b] Þ

a)            se D₁ è più fine di D₂ si ha che  s(D₂,f) £ s(D₁,f) £ S(D₁,f) £ S(D₂,f)

b)            s(D₁,f) £ S(D₂,f)

a) Per dimostrare che s(D₂,f) £ s(D₁,f) supponiamo che D₁ abbia solo un punto z in più rispetto a D₂ pertanto esisterà un k compreso tra 1 ed n tale che il punto z è compreso nell´intervallo (x_K-1 , x_K) pertanto non si fa altro che scrivere s(D₂,f) come somma di 3 termini di cui il 1° è la somma inferiore sino al punto che precede k, il 2° termine è il prodotto della intervallo (x_K-1 , x_K) per il minimo sull´intervallo stesso ed il 3° termine è la somma inferiore da k+1 sino ad n. Ossia

      Si osserva poi che il 2° termine è sicuramente £ del termine che otterremmo quale somma inferiore sulla sottosuddivisione (x_K-1 , z, x_K) in quanto più fine rispetto alla (x_K-1 , x_K) ed osservando che l´unione di questa sottosuddivisione più fine con il 1° ed il 3° termine non è che s(D1,f) , che analoga dimostrazione si può fare per le somme superiori e che in generale si ha , risulta dimostrata la parte a) del teorema.

b) Si deve dimostrare che s(D₁,f) £ S(D₂,f) , se le 2 suddivisioni sono confrontabili questo è sempre vero (come dimostrato nella parte a) del teorema), se invece le 2 suddivisioni non sono confrontabili allora si può prendere una suddivisione D₃ : = D₁ È D₂ che è più fina di entrambe ed affermare in base alla parte a) del teorema che

      s(D₁,f) £ s(D₃,f) ed anche S(D₃,f) £ S(D₂,f)  e dato che per ogni suddivisione D si ha s(D,f) £ S(D,f) in definitiva conglobando queste 3 disuguaglianze si ha s(D₁,f) £ S(D₂,f) ed il teorema è dimostrato.

 

2) Se f è una funzione limitata in un intervallo [a,b] Þ

                f Î Â(a,b)              Û            " e  $ una suddivisione D_e di [a,b] tale che S(D_e ,f)- s(D_e ,f) < e

Þ  Se fÎ Â(a,b) allora  e per definizione di inf si avrà che preso un e > 0  $ una suddivisione D_e‘ tale che S(D_e‘ ,f) < I + e / 2  ed una suddivisione D_e‘´ tale che s(D_e‘´ ,f) > I - e / 2  . In definitiva prendendo una suddivisione D_e : = D_e‘ È D_e‘´ si avrà che

S(D_e ,f)- s(D_e ,f) £ S(D_e‘´,f)- s(D_e‘,f) < I(f) + e / 2 - I(f) - e / 2 = e .

Ü  Si ha l´integrabilità secondo Riemann allorché la differenza tra l´estremo superiore delle somme inferiori e l´estremo inferiore delle somme superiori, tende a 0, il che si ottiene considerando che tale differenza è compresa tra 0 e la differenza S(D_e ,f)- s(D_e ,f) < e la quale si può rendere piccola a volontà operando su di e.

3) Se f è una funzione continua nell´intervallo [a,b]                 Þ          f Î Â(a,b)

Si osserva che una funzione continua su di un intervallo limitato è anche uniformemente continua sullo stesso pertanto per ogni e > 0 si può trovare un d > 0 tale che presi 2 punti qualsiasi nel dominio la cui distanza reciproca sia minore di d , si ha che le loro immagini si trovano a distanza inferiore ad e / b-a . Basta pertanto scegliere una suddivisione D_e la cui ampiezza |D_e| sia minore di d e si potrà riscontrare che la differenza tra il Min ed il Max sul singolo intervallino è minore di e / b-a  e conseguentemente anche la differenza tra le somme superiori e le somme inferiori risulterà minore di e infatti   e ricordando che se S(D_e ,f)- s(D_e ,f) < e allora f Î Â(a,b) ne consegue che il teorema è dimostrato.

 

4) Se f è una funzione monotona nell´intervallo [a,b]                              Þ          f Î Â(a,b)

L´idea della dimostrazione è di riportarci a poter affermare che " e > 0 $ D_e , suddivisione di [a,b] : S(D_e ,f)- s(D_e ,f) < e

Parto quindi dal 1° membro di quest´ultima e dimostro che è minore di e :

in quanto ipotizzando la funzione monotona crescente                                                                                                             si ha f(x_i) ³ M_i      e      f(x_i-1) £ m_i

  in quanto |D_e| è la ampiezza del più grande intervallo                                                                                                               della suddivisione.

  in quanto l´immagine di una funzione monotona crescente è                                                                                                                         limitata dai 2 valori assunti agli estremi della intervallo.

Scegliendo pertanto la suddivisione D_e in modo che  si ha S(D_e ,f)- s(D_e ,f) < e allora f Î Â(a,b).

 

5) Se f è una funzione limitata nell´intervallo [a,b]    ed ha un n° finito di punti di discontinuità    Þ          f Î Â(a,b)

L´idea della dimostrazione è di riportarci a poter affermare che " e > 0 $ D_e , suddivisione di [a,b] : S(D_e ,f)- s(D_e ,f) < e

      e pertanto fÎÂ(a,b). Supponiamo che il punto di discontinuità sia ad un estremo, ad esempio a e considerando xÎ(a,b) si ha che nell´intervallo [x,b] f è continua fÎÂ(x,b) ossia " e > 0 $ una suddivisione D_e‘ tale che si ha

      S(D_e‘ ,f) - s(D_e‘ ,f) < e / 2. Nell´intervallo [a,x] invece si ha

        in quanto per la proprietà di completezza se f è limitata allora ammette                                                                            inf e sup e supponiamo K = sup | f |.

         avendo scelto il punto x tale che

      scegliendo quindi come suddivisione D_e = D_e‘ È {a} si ha :

     S(D_e ,f) - s(D_e ,f)      =    (M₁ - m₁)(x -a) + S(D_e‘ ,f) - s(D_e‘ ,f)    <         e dunque il teorema è dimostrato.

 

6) Se f è una funzione limitata nell´intervallo [a,b]    Þ f è integrabile secondo Riemann Û esiste LÎÂ per il quale "

                e > 0  " un d>0 tale che " suddivisione D la cui ampiezza sia |D| < d risulta |s(D,f) - L |< e .

 

7) Se f e g sono funzioni integrabili             Þ           af + bg  è una funzione integrabile in (a,b) e vale la :

Si può osservare che

a) l´estremo superiore della funzione somma è £ della somma degli estremi superiori delle singole funzioni

b) l´estremo inferiore della funzione somma è ³ della somma degli estremi inferiori delle singole funzioni.

c) Moltiplicando le somme inferiori e le somme superiori per la stessa costante l´integrale che ne è la differenza non può che essere costante.

 

8) Se f e g sono funzioni integrabili ed f £g               Þ          

Occorre dimostrare che l´integrale della funzione h(x) := g(x) - f(x) è ³ 0 , il che discende dal fatto che h(x) ³ 0 in quanto g(x) ³f(x) dunque anche l´estremo inferiore di h è non negativo e ricordando la disuguaglianza multipla si ha che  ed il teorema è dimostrato.

 

9) Se f e una funzione integrabile                 Þ          

                a) f₊ è integrabile

                b) f _- è integrabile

                c) |f| è integrabile

                d) Si ha che  , in particolare si ha

a) Affinché f₊ sia integrabile si deve dimostrare che " e > 0 $ D_e  tale che S(D_e ,f₊)- s(D_e ,f₊) < e , per far ciò si sfrutta il fatto che f è integrabile e quindi S(D_e ,f)- s(D_e ,f) < e . Si ha :

dove si è sfruttata la proprietà evidente di f₊ secondo la quale    .

b) Che f _- sia integrabile si dimostra in maniera analoga a quanto fatto per f₊ .

c) Si dimostra ricordando che | f | = f₊ + f _- ed applicando il teorema 120) per la composizione di funzioni integrabili.

d)                                 infatti       f = f₊ + f _-

                       dove ho applicato la disuguaglianza triangolare

   

     nell´ultima ho utilizzato che f₊ ed f _- sono funzioni positive e dunque anche i loro integrali , e che  | f | = f₊ + f _-   .

 

10) Se f e una funzione integrabile in (a,b) e c Î (a,b) allora f è integrabile anche su (a,c) e su (c,b) e risulta :

a) Dimostrazione che fÎÂ(a,c) e fÎÂ(c,b)

      Se f è integrabile su una suddivisione D, allora lo è a maggior ragione su di una suddivisione D_e più fine quale si ha aggiungendo a D il punto c. Avremo quindi le seguenti suddivisioni : D_e‘ := D_e È(a,c)   e    D_e‘´ := D_e È(c,b)

      varrà pertanto la seguente uguaglianza :

      ma f è integrabile lungo la suddivisione D_e quindi   e dovrà quindi essere :

                                        Þ                           f Î Â(a,c)

                                       Þ                           f Î Â(c,b)

b) Dimostrazione che

       in quanto  vengono utilizzate 2 suddivisioni più fine di D_e . Del resto si ha

      e dunque per la arbitrarietà di e il teorema è dimostrato.

 

 

11) Teorema della media :

Descrizione :  Se f è una funzione integrabile in (a,b) ed m è l´inf mentre M è il sup sempre su di (a,b)    Þ

               inoltre se f è continua Þ $ c per il quale

Ricordando la disuguaglianza   e  dato che per ipotesi del teorema f è integrabile quindi s(D,f) = S(D,f) si ha che  e dividendo per (b-a) il teorema è dimostrato.

Per dimostrare la 2ª parte basta considerare che l´immagine di una funzione continua definita su di un intervallo è ancora un intervallo e quindi $ c tale che .

 

12) Se f è una funzione integrabile in (a,b) e continua in x₀ Î (a,b) e c Π (a,b) allora la funzione integrale

                 è derivabile in x₀ e risulta F´(x₀) = f(x₀).

Essendo f continua in x₀ si ha che " e > 0 esiste d > 0 tale che |x-x₀| < d    e  | f(x) - f(x₀) | < e  cioè

f(x₀)-e < f(x) <  f(x₀)+e    ed avendo dimostrato che se f(x) > g(x) allora , si può scrivere :

 

dividere tutto per (x-x₀) ed ottenere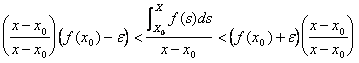 

In quanto f(x₀)+e  e f(x₀)-e   sono costanti.

Del resto 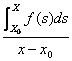=  infatti si ha :

in definitiva quindi si ottiene  ossia  F´(x₀) = f(x₀).

 

13) Teorema fondamentale del calcolo integrale :

Descrizione :   Se f è una funzione continua su [a,b]  Þ

                  a) la funzione integrale è derivabile su tutto [a,b] e la sua derivata è f(x) per ogni x Î [a,b].

                  b) Se G è una primitiva di f in [a,b]   Þ        

a) Segue semplicemente dalla dimostrazione precedente quale osservazione che stavolta la f non è continua in un sol punto bensì in ogni punto di [a,b] e pertanto la funzione integrale sarà derivabile su tutto (a,b) e la sua derivata sarà f.

b) prendendo un punto c interno al segmento [a,b] si può scindere  e siccome le primitive differiscono unicamente a meno di una costante questa si elide con il - pertanto sarà anche  ed il teorema è pertanto dimostrato.

 

Integrali dipendenti da un parametro

14) Se f è una funzione continua in [a,b]x[c,d] Þ   è continua su [c,d] e

a)                quindi si può calcolare unicamente l´integrale del limite

b)            Se f ed f_Y sono continue su [a,b]x[c,d] Þ j Î C´([c,d])  e

a) Occorre dimostrare che | f(y) - f(y₀)| < e  a tal fine si sostituisce la definizione di f per ognuna delle 2 la si maggiora con il modulo portato sotto il segno di integrale ossia :   e ricordando che la funzione f è continua su di un compatto si ha che è anche uniformemente continua pertanto " e > 0 esiste d > 0 tale che per ogni coppia y , y₀ Î[c,d] con |y-y₀|<d si ha che   Che sostituito nel precedente ultimo integrale restituisce  se |y-y₀| < d  e quindi  | f(y) - f(y₀)| < e .

b) Partendo dal rapporto incrementale della funzione j(y) utilizzando la definizione di quest´ultima si ottiene :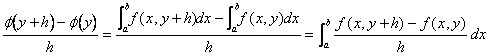

      Applicando il teorema del valor medio si ha che $q Î(0,1) per il quale   

      ed aggiungendo e sottraendo f_Y(x,y) si ottiene  . Avendo ipotizzato f_Y continua e quindi anche uniformemente continua visto che è definita su di un compatto si elimina   ottenendo

 

15) Se f  e f_Y sono continue in [a,b]x[c,d] ed a e b sono 2 funzioni aventi derivata prima continua in [c,d]   Þ la funzione   ha derivata 1ª  continua su [c,d] e

Integrabilità in senso improprio

16-a) Criterio del confronto

             Siano f ,g : [a,b)®Â con bÎÂ^* , integrabili secondo Riemann " w Î [a,b), inoltre sia  0 £ f(x) £ g(x) " xÎ[x₀,b)                Þ           se g è integrabile in senso improprio in [a,b)   Þ  f  è integrabile in senso improprio.

f è integrabile in senso improprio se esiste finito

Il 1° integrale a secondo membro esiste finito in quanto la funzione è integrabile secondo Riemann " w Î[a,b).

Del 2° integrale si deduce che essendo f positiva, è una funzione monotona crescente, pertanto ammette limite e questo limite sarà finito in quanto se f £ g anche   e del resto   in quanto g(x) è integrabile in senso improprio.

 

16-b) Criterio del confronto

                Siano f ,g : (a,b]®Â con aÎÂ^* , integrabili secondo Riemann " w Î (a,b], inoltre sia  0 £ f(x) £ g(x) " xÎ(a,x₀]              Þ           se g è integrabile in senso improprio in [a,b)   Þ  f  è integrabile in senso improprio.

 

17-a) Intervallo non limitato

Sia f :[a,+¥)®Â  definitivamente positiva per x®+¥   ed     fÎÂ[a,w)   per ogni   w > a  Þ

a)            se f è infinitesima di ordine a>1 rispetto ad 1/x per x®+¥   Þ   f è integrabile in senso improprio in [a,+¥).

b)            se f è infinitesima di ordine a£1 rispetto ad 1/x per x®+¥   Þ   f non è integrabile in senso improprio in [a,+¥).

 

17-b) Funzione non limitata

Sia f :[a,b)®Â   bΠ definitivamente positiva per x®b ^-   ed   fÎÂ[a,w)   per ogni   w Î(a,b) Þ

a)            se f è infinita di ordine a<1 rispetto ad 1/(b-x) per x® b ^-   Þ    f è integrabile in senso improprio in [a,b).

b)            se f è infinita di ordine a³1 rispetto ad 1/(b-x) per x® b ^-   Þ    f non è integrabile in senso improprio in [a,b).

 

18) Se f è definita su di un intervallo I e | f | è integrabile in senso improprio in I Þ  f è integrabile in senso improprio e

Per dimostrare che f è integrabile in senso improprio basta applicare il teorema del confronto utilizzando |f| per stabilire che anche f ₊ ed f  _- sono integrabili in senso improprio e quindi anche f essendo f = f ₊ - f  _- .

Per la formula invece si ha : Dove si è utilizzato :

a) f = f ₊ - f  _{-      .}

b) la disuguaglianza triangolare.

c) f₊ ed f_- sono funzioni positive, quindi anche i loro integrali, e pertanto i moduli sono inutili.

d) | f | = f ₊  +   f  _{-    .}