Teoremi sulle funzioni di 2 variabili
Funzioni di 2 variabili
1) Se f è differenziabile in xÎX insieme aperto (ossia se esiste a ÎÂn tale che f(x+h) = f(x) +<a,h> +o(||h||) per h®0) Þ
a) f è continua in x
b) esistono le derivate parziali di f in x e si può scrivere : f(x+h) = f(x) +<Ñf(x),h> +o(||h||) per h®0
c) esistono le derivate direzionali Dvf(x) per ogni versore e vale la formula Dvf(x) = <Ñf(x),v>
a) Dalla definizione di differenziabilità inserendo i moduli si trae |f(x+h) - f(x)| = |<a,h> +o(||h||)| per h®0 . Applicando la disuguaglianza di Cauchy-Schwarz (ossia |<a,h>| £ ||a|| * ||b|| ) al 2° membro si ottiene |<a,h> +o(||h||)| £ ||a||*||h|| ® 0 per h®0, pertanto f è continua essendo |f(x+h) - f(x)| < e.
b) Nella definizione di differenziabilità si sostituisce t*eK ad h e si ottiene che (f(x + t*eK)-f(x))/t = <a , eK> sfruttando il fatto che ||eK|| = 1 essendo la base canonica costituita da versori. pertanto la derivata nella direzione xK della base canonica è pari al componente k-esimo di a e dunque si può porre a = Ñf(x).
c) Nella definizione di differenziabilità si sostituisce t*v ad h e si ottiene che (f(x + t*v)-f(x))/t = <a , v> sfruttando il fatto che ||v|| = 1 essendo v un versore. Pertanto la derivata direzionale lungo una qualsiasi direzione v è pari al prodotto scalare tra il gradiente di f(x) ed il vettore v.
2) f è una funzione derivabile in xÎX aperto Þ
f(x+h) = f(x) + <Ñf(x),h> + o(||h||) per h®0 Û f è differenziabile in x
Þ La derivabilità di f in x consente di sostituire Ñf(x) nella f(x+h) = f(x) + <a,h> + o(||h||) per h®0 e ritroviamo la definizione di differenziabilità in x.
Ü La differenziabilità implica la validità della f(x+h) = f(x) + <Ñf(x),h> + o(||h||) come descritto dal 101-b)
3) Teorema del valor medio per funzioni di più variabili:
Descrizione : Se f è una funzione continua su di un segmento [x,y] Í X allora :
a) Se v = (y-x) / ||y-x|| è un versore di questo segmento ed esiste la derivata direzionale lungo v per ogni punto appartenente al segmento Þ esiste un q0 compreso tra 0 ed 1 tale che
f(y) - f(x) = Dv f((1-q0)x + q0y) * || y-x ||.
b) Se inoltre f è differenziabile in ogni punto del segmento Þ esiste un q0 tale che
f(y) - f(x) = < Ñf((1-q0)x + q0y) , y-x >.
a) Ci si riporta ad applicare il teorema del valor medio lungo la direzione v tramite la funzione jv(t) := f(x + tv) la quale consente di trattare una funzione di 2 variabili come una funzione di una variabile. di essa si osserva che :
j‘(t0) = Dv f(x + t0v) , j(0) = f(x) , j(||y-x||) = f(y)
pertanto applicando il teorema del valor medio unidimensionale si trova che esiste un t0 per il quale
f(y) - f(x) = j(||y-x||) - j(0) = jv´(t0) * ||y-x|| = Dv f(x + t0v) * ||y-x||
e ponendo q0 = t0 / || y-x || si ottiene l´enunciato del teorema.
b) Dalla parte a del teorema sappiamo che f(y) - f(x) = Dv f((1-q0)x + q0y) * || y-x || mentre dalla differenziabilità consegue che vale la formula Dvf(x) = < Ñf(x),v > , sostituendola si ha che :
f(y) - f(x) = < Ñf((1-q0)x + q0y) , v > * || y-x ||
ed essendo v = (y-x) / ||y-x|| ne consegue il teorema.
4) Teorema del differenziale totale:
Descrizione : Se esiste un intorno U di x nel quale f è derivabile(esistono tutte le derivate parziali in x) e se le derivate parziali sono continue nel punto x Þ f è differenziabile in x.
Dobbiamo provare che f(x) è differenziabile, ossia che e f(x+h) = f(x) + <Ñf(x),h> + o(||h||) per h®0 o analogamente si può dimostrare che la funzione ![]() ® 0 oppure per esteso
® 0 oppure per esteso
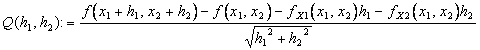 ® 0
® 0
A tal fine si prendono i primi 2 termini del numeratore e tramite il teorema del valor medio per funzioni di più variabili applicato lungo le direzioni dei versori della base canonica, ci si riporta ad avere fx1 ed fx2 da poter raccogliere.
f(x1 + h1 , x2 + h2) - f(x1 , x2) = [f(x1 + h1 , x2 + h2) - f(x1 , x2 + h2)] + [f(x1 , x2 + h2) - f(x1 , x2)]
ed applicando il teorema del valor medio lungo e1 ed e2 ai termini contenuti in ciascuna delle 2 quadre, si ottiene che :
f(x1 + h1 , x2 + h2) - f(x1 , x2) = fx1(x1 + q1h1 , x2 + h2)h1 + fx2(x1 + q1h1 , x2 + h2)h1
la quale sostituita nella definizione di Q e raccogliendo h1 ed h2 restituisce :
![]() ed essendo i termini
ed essendo i termini  e
e 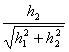 entrambe non maggiori di 1 e per ipotesi del teorema continue entrambe le derivate parziali allora si avrà che quando h®0 , Q(h1,h2)®0 e pertanto il teorema è dimostrato.
entrambe non maggiori di 1 e per ipotesi del teorema continue entrambe le derivate parziali allora si avrà che quando h®0 , Q(h1,h2)®0 e pertanto il teorema è dimostrato.
5) Se f è 2 volte differenziabile in xÎX insieme aperto Þ fX nX m (x) = fX mX n (x) "m, n = 1,..., n
6) Se f è m volte differenziabile in xÎX insieme aperto e dx è tale che il segmento [x+dx]Í X allora
a) Vige la formula di Taylor con il resto di Peano ![]() per dx®0
per dx®0
e ![]() è l´unico polinomio di grado £ m che la verifica.
è l´unico polinomio di grado £ m che la verifica.
b) Se inoltre f è m+1 volte differenziabile in (x+dx) allora esiste q0 tale che :
![]()
a) In sostanza si deve verificare che ![]() o equivalentemente che
o equivalentemente che ![]() .
.
Ricordando che il polinomio di Taylor è tale che fK(x0) = TnK(x0) segue che h(x0) = 0 e si può applicare il teorema del valor medio: h(x+dx)=h(x+dx)-h(x) = Dvh(c)||dx|| = <Ñf(c),dx> = ![]() e ricordando la disuguaglianza triangolare
e ricordando la disuguaglianza triangolare 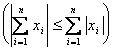 si ha
si ha
|h(x+dx)| = ![]() si deve quindi solo dimostrare che
si deve quindi solo dimostrare che ![]() il che si ottiene per induzione dal teorema stesso, infatti si ha :
il che si ottiene per induzione dal teorema stesso, infatti si ha :
p0 ® Il teorema è vero per m=1 in quanto si ritrova la definizione di differenziabilità
p1 ® Si suppone il teorema valido sino a m-1, pertanto applicandolo ad hxi si ha:
hxi (x+dx) = hxi (x ) + ![]() per dx ® 0
per dx ® 0
infatti le hxi sono m-1 volte differenziabili ed hanno le derivate di ordine £ m nulle in x0 , si ha quindi
hxi(x+dx) = o(||dx||m-1) Þ hxi(x+qdx) = o(||qdx||m-1).
Sostituendo questo risultato nella [1] il teorema è dimostrato, infatti si ha :
h(x+dx) = ![]() £
£ ![]() =
= ![]()
L´unicità del polinomio di Taylor si dimostra considerando un P(x+dx) di grado £ m tale che
f(x+dx) = P(x+dx) + o(||dx||m) per dx®0 , del resto è anche f(x+dx) = Tm(x+dx) + o(||dx||m) , uguagliando si ha :
P(x+dx) - Tm(x+dx) = o(||dx||m e dato che entrambe i polinomi sono di grado £ m ne consegue che o(||dx||m non è in grado di assorbire nessun termine degli stessi e dunque P(x+dx) = Tm(x+dx).
b) La formula di Taylor con il resto di Lagrange si dimostra in maniera equivalente riportandosi al caso unidimensionale dove poter applicare la formula già nota, in particolare si utilizza la jv(t) = f(x+tv) alla quale è applicabile il resto di Lagrange unidimensionale, per le sue derivate si ha :
jvk (t) = Dkvv....v f(x+tv) se 0 < t < ||dx|| jvm+1 (t) = Dm+1vv....v f(x+tv) se 0 < t < ||dx||
applicando quindi il teorema di Lagrange unidimensionale:
jv(||dx||) = jv(0) +![]()
e dato che il differenziale df(x) si presenta nella forma dKf(x) = f K(x) (dx)K e sostituendo il teorema è dimostrato.
7) Se f è una funzione convessa su di un insieme A convesso ed aperto Þ
a) f è continua in A ed ammette derivate parziali destre e sinistre in A.
b) se f è derivabile in un punto xÎA Þ f è anche differenziabile in x.
8) Se f è una funzione differenziabile in xÎA insieme convesso ed aperto Þ
a) se f è convessa Þ f(x) ³ f(x0) + <Ñf(x0) , x-x0> per ogni xÎA
b) se f è strettamente convessa Þ f(x) > f(x0) + <Ñf(x0) , x-x0> per ogni xÎA , x ¹ x0 .
Si applica il risultato ottenuto per le funzioni convesse in una variabile f(x) ³ f(x0) + f ‘(x0)(x-x0) tramite la funzione
jv(t) = f(x+tv) essendo jv(0) = f(x0) , jv(||x-x0||) = f(x) e jv´(x0) = Dvf(x) ed avendo dimostrato che per una funzione differenziabile si ha Dvf(x) = < Ñf(x) , v > scegliendo t = || x - x0 || , ![]() e sostituendo, il teorema è dimostrato.
e sostituendo, il teorema è dimostrato.
9) Se f è una funzione differenziabile in ogni punto x della insieme A, convesso ed aperto Þ
a) f è convessa Û f(x) ³ f(x0) + <Ñf(x0) , x-x0> per ogni x0ÎA .
b) f è strettamente convessa Û f(x) > f(x0) + <Ñf(x0) , x-x0> per ogni x0ÎA .
10) Se f è una funzione 2 volte differenziabile in ogni punto x della insieme A, convesso ed aperto Þ
a) f è convessa in A Û d2f(x) = <Hf (x)dx , dx> ³ 0 per ogni dx Î Ân .
b) f è strettamente convessa in A se per ogni xÎA si ha <Hf (x)dx , dx> > 0 per ogni dxÎÂn e dx ¹0.
Utilizzando la formula di Taylor con il resto di Lagrange ![]() sostituendo per m =1si ha che esiste un qÎ (0,1) tale che
sostituendo per m =1si ha che esiste un qÎ (0,1) tale che ![]()
che si può anche scrivere ![]() ³ 0 in quanto essendo la funzione convessa si ha che f(x) ³ f(x0) + <Ñf(x0) , x-x0> .
³ 0 in quanto essendo la funzione convessa si ha che f(x) ³ f(x0) + <Ñf(x0) , x-x0> .
11) Se f è una funzione 2 volte differenziabile in ogni punto x della insieme A, convesso ed aperto Þ
a) f è convessa in A Û Hf (x) è semidefinita positiva per ogni x Î A .
b) f è strettamente convessa in A Û Hf (x) è definita positiva per ogni x Î A .
12) Se f è differenziabile in xÎA aperto ed x è punto di estremo locale per f Þ x è un punto critico cioè Ñf(x) = 0
Si ponga però attenzione al fatto che un punto critico non è necessariamente un estremo locale, oppure se f non è differenziabile in x0 , x0 può essere punto di estremo oppure no.
13) Se f è un insieme convesso ed x è un punto critico di f allora :
a) Se esiste un intorno di x nel quale f è convessa Þ x è punto di minimo di f.
b) Se esiste un intorno di x nel quale f è concava Þ x è punto di massimo di f.
Inoltre se f è 2 volte differenziabile in x allora :
c) Se Hf (x) è definita positiva Þ x è un punto di minimo forte di f.
d) Se Hf (x) è definita negativa Þ x è un punto di massimo forte di f.
e) Se Hf (x) non è semidefinita positiva ne semidefinita negativa Þ x è un punto di sella di f.
f) Se Hf (x) è semidefinita positiva o semidefinita negativa Þ x è di sella o di massimo o di minimo per f.
a) f differenziabile e convessa implica che la funzione sia tutta sopra al piano tangente in x e pertanto questi non può che essere un punto di minimo .
b) f differenziabile e concava implica che la funzione sia tutta sotto al piano tangente in x e pertanto questi non può che essere un punto di massimo .
c) Si può applicare il teorema di Peano ![]() tenendo conto che il punto critico in x implica che il gradiente è nullo e pertanto anche il differenziale, df(x) = <Ñf(x),dx> = 0 , la formula diviene
tenendo conto che il punto critico in x implica che il gradiente è nullo e pertanto anche il differenziale, df(x) = <Ñf(x),dx> = 0 , la formula diviene ![]() e considerando che se la matrice Hessiana è definita positiva allora la autovalore più piccolo è positivo si può minorare f(x) e dire
e considerando che se la matrice Hessiana è definita positiva allora la autovalore più piccolo è positivo si può minorare f(x) e dire ![]() e pertanto per dx®0 ossia in un intorno molto piccolo di x si ha che la funzione assume valori maggiori che non in x che pertanto è un punto di minimo.
e pertanto per dx®0 ossia in un intorno molto piccolo di x si ha che la funzione assume valori maggiori che non in x che pertanto è un punto di minimo.
d) Si dimostra analogamente al punto c).
e) In ogni intorno di x si ha che Hf è semidefinita positiva per alcuni vettori e semidefinita negativa per altri vettori ossia per meglio dire non è ne semidefinita positiva ne semidefinita negativa pertanto vi sono valori per cui il differenziale è positivo e valori per i quali il differenziale è negativo e pertanto punti in cui la funzione è maggiore che non in x e punti in cui la funzione è minore che non in x pertanto x è un punto di sella.
f) Si dimostra con un esempio pratico, ossia si prendono 3 funzioni ( x14 + x24 ) , ( x14 - x24 ) e -( x14 + x24 ) aventi tutte e tre la stessa matrice hessiana costituita da tutti 0 e lo stesso punto critico (0,0) e si dimostra che per la 1ª è un punto di minimo, per la 2ª è un punto di sella mentre per la 3ª è un punto di minimo.
