Analysis of not linear circuits to microwaves

1) Tension v(t) of a circuit RC parallel fed from a current generator:

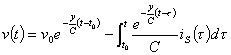The expression in the dominion of the time is obtained resolving the equation differentiates them that supplies . One can be had also expression in terms of fasori from which .

 

 

 

2) directed numerical Solution of the :

The equation differentiates them not linear comes discretizzata in the dominion of the time, the equation that turns out some can assume the two following shapes:

to) 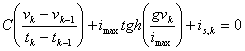in this case it is necessary a value begins them for being able to calculate iterativamente the other values then, however a imprecisione is inborn in how much the linearity does not preview the acquaintance of v_k and therefore a not linear equation will have to be resolved in which the solution is in implicit shape, it comes found with methods iterati to you like that one of Newton. The error can be rendered small to appeals to reducing the discretizzazione interval.

b) 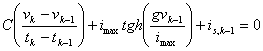in this case if v_k-1 it is famous can resolve for v_k in how much the equation becomes to delineate in the incognito. The stability of the solution cannot be guaranteed even if renders the discretizzazione interval very small.

The discretizzazione step can be rendered uniform or less, in kind a uniform step for the permanent regimen convene while for transitory where there are the more abrupt variations a tightened step convene more.

 

 

3) Solution by means of expansion in series of the :

In alternative to the temporal discretizzazione they can be made of the hypotheses on the solution like demanding that he is esprimibile in series of powers and that this series is troncabile so as to to maintain the greater part of the information, to the end the equation for every term of the series will have to be resolved.

 

4) Series of Volterra:

It is an extension of the integral of convoluzione to the not linear circuits, has dove h_n is the transformed nucleus of order n having of generalized Fourier . In I dominate of Fourier the series of Volterra assumes the shape , achieves some that the phantom of marks them of escape is various from the phantom of marks them of income.

In the case of it marks them of real income the nucleus of second order from place to a term rectified beyond that to the harmonica of second order.

5) Probing Method:

Draft of a method that concurs to determine the nuclei of the system, the application steps are following:

to)       the answer is applied to an ideal tone is arresting itself for semplicità to according to order and replacing it in the equation it differentiates them that it describes to the containing circuit the nonlinearity expressed in series of powers, obtains a containing equation terms to various frequencies, it must be verified for every frequency, from the equality to the fundamental frequency obtains the nucleus of order 1.

b)       In order to gain the general term of order 2 we apply two ideal tones , stavolta is had: we consider the single terms that contain the nucleus of order 2 in the more general shape contain that is are f₁ that f₂

c)       the other terms in iterativa way are gained

Naturally the method demands that the linearity is not expressed in terms of series of powers and that the linearity is not light otherwise the calculation of the nuclei turns out impraticabile.

 

6) 1dB Compression Point:

It is the value of the power in income for which the power in escape is worth 1dB in less regarding the value of the power of escape in saturation.

 

7) Intercept Point:

In the plan in dB that alloy the power in escape to the power in income, we have a straight one to unitary slope for the term of first degree and of the straight ones with various slopes for the terms of the other degrees, the intercept point that they are used in kind they are those between straight relative to the first degree and those relative ones to 2° the degree and 3° the degree.

 

8) Problems legacies to the intermodulazione:

The contributions of the intermodulazione fall in the band of mark them of income and therefore it is not possible to filter them.

 

9) Problems legacies to the desensitivizzazione:

It comes embezzled power to the fundamental one and redistributed on the phantom, that makes that in the case more tones the jam arrives before.

 

10) Series of Fourier:

In this case the incognito comes expressed in series of Fourier and replaced in the equation it differentiates them that it describes the circuit, for every term of the series obtains a algebrica equation, us can be limited to an ended number on condition that the first terms of the series are in a position to describing the function adequately.

The real part of the equations can be calculated in immediate way multiplying for an opportune matrix while the not linear part must be calculated in the dominion of the time and then transformed.

It is like subdividing the circuit in linear part and not linear part after which the currents for every harmonica are equaled, gives them equations that are obtained can be gained the incognito by means of the method of Newton.

The method concurs of dealing also circuits with forts linearity however is not possible the analysis of the transitory one and with it marks them of income complex.