Synthesis of passive nets
1) Stiffness driving-point of one net and functions of energy:
The equations of Kirchoff to the nodes can be written in
matriciale shape 
where i(t) it is the carrier of
the currents and To it is the incidence matrix which transposed
relaziona also the carrier v(t) of the tensions to coppers with the
carrier vn(t) of the tensions to
the 
nodes. through these relations it is
reached the expression of the 
power where b the
circuit is the number of constituent coppers, the transformed one of
Laplace is 
from which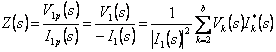 
that in
the case of a net LC rewrites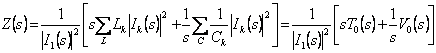 
being T0(s) e V0(s) functions of energy that they are always real and not
negative.
2) Property of functions LC driving-point:
The zeroes are found on the axis jw in fact placing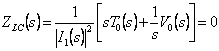 
trova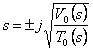 
that is imaginary in how much the functions of
energy 0T 0 andV are real and positive.
Reasoning on the function admittance an analogous result for its
zeroes is found and therefore poles and zeroes of immettenze LC
driving-point find on the imaginary axis, they moreover are simple and
they are alternated in fact imposing sinusoidale stationary state s = 0 obtains 
that is the stiffness it becomes pure imaginary and it is said
reattanza and its derivative is 
e
therefore X(w) is monotonous
increasing that it is possible single if poles and zeroes are simple and
they are alternated. It is had moreover that the behavior in the
origin or to infinite is that one of a pole or a zero that implies
that numerating and denominator must differ for 1 degree. Based
on the previous reasonings can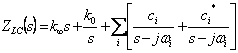 
be written where
the c must real and be positi to you.
3) Synthesis of functions LC driving-point:
to) Methods of Foster
If we must synthetize one function 
stiffness enough to put in series one inductance of 
value, a condenser of 
value and
some parallels of inductances of 
value and
condensers of 
value with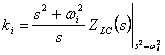 
.
If we must instead synthetize one function 
admittance enough to put in parallel one value
inductance 
, a condenser of value K¥ and some series of inductances of
value and condensers of value .
The methods of Foster are canonical realizations in how much use the minimal possible number of elements.
b) Shapes of Cauer
They are two methods bases to you on I use of the continuous fractions and on the fact that rimuovendo from a LC-realizable function a pole in the origin or a pole to the infinite still obtains one LC-realizable function
b1) removal of the poles to the infinite
If ZLC(s) has a pole to the infinite the realizing circuit
has an inductance in series of 
value, rimuovendo
this pole remains a function ZLC with a pole in the origin which 1 = 1/ Z LC having correspondsa Y a pole to the infinite
that can be removed and to which a condenser in parallel with value
corresponds 
, is continued cos¬ until has not been
realized all the function Z3(s).
b2) removal of the poles in the origin
If ZLC(s) has a pole in the origin the realizing circuit has a condenser in value series 1/a, it is removed and it is continued R-come.sopra.
4) Poles of transfer functions:
For a net LC the poles of the transfer function are simple
and they are found on the axis jw, for nets RC and RL they are simple and they find on not
simple the real axis negative while for nets RLC they are ovunque and
also. All the poles of the functions driving-point are not
present in the transfer functions, those not present are said private
poles while all the poles on the axis jw of the transfer function must be present in the functions
driving-point in how much must verify the condition on residual 
the where kij it is
the residual one of zij(s) in
pole s = jwi .
The poles not pertaining to the axis jw can also not be present in the functions driving-point.
5) Condition of Fialkow:
Every scale net of admittances pu² to be reduced to a
net p constituted from not
negative admittances by means of transformations t " p, has 
, 
, 
, if of it it deduces the condition of second
Fialkow which the coefficients of the numerator of â?"y12(s) must not be denied to you and
more small regarding you respect 22 coefficients to you ofy11 (s) andy(s), follows some that us they cannot
be zeroes on the axle shaft positive.
6) adimensional Functions of transfer:
where P(s) contains the private poles of the function
driving-point and 11N(s)
its zeroes while 21N(s)
contains the zeroes of the transfer function. The coefficients of
the numerator and those of the denominator are then subject to the
condition of Fialkow. Analogous considerations are applied then
to 
the .
7) Conditions on the real part of the parameters of one passive net:
such conditions derive from the fact that a value negative of these you leave real would imply energy supplied from the net to the generator that passive net is not possible for one.
8) Zeroes of the scale nets:
We consider a scale net constituted from a stiffness shunt
Z1 , a stiffness series Z2 and a passive net zij', the transfer function is 
from which evince that the zeroes of transmission of a
scale net are produced from the zeroes of the stiffnesses shunt and from
the poles of the stiffnesses series and they are found therefore in
the left semiplan and on the axis jw .
9) Synthesis of transfer functions using scale nets without losses:
The polinomi of Hurwitz they have all the positive
coefficients you and not null and the zeroes are all in the left
semiplan, one they important property is that the relationship of the
equal part with the uneven part or viceversa is realizable as one
immettenza LC driving-point. Considering a net LC sluice on a
resistore the poles can be ovunque in the left semiplan therefore the
denominator of the transfer function are a polynomial of Hurwitz while
the zeroes are on the axis jw,
have 
of it derive that if N(s) is equal then 
ed 
and y22(s) is LC-realizable as pure
if N(s) is uneven it has 
e 
y the 22 If(s) to realize possesses of the private poles regarding ythe 21(s) then these will go
removed adding to the circuit the element adapted to represent
them.
10) Synthesis of functions of transfer with zero shifting:
In the case that the zeroes of the transfer function are
posizionati ovunque in symmetrical braces on the axis jw , the technique of the movement of
the zeroes is used that consists in diminishing the power of the pole to
the infinite sottraendogli a 22 amount so as to to make
thaty21 (s) andy(s) have the same zeroes . This
technique comes used in order to realize the elliptic
Chebyshev-Inverso approximations and which demand zeroes on the axis jw . In the practical one
a term Y 0 = Ksmustbe embezzled to ythe 22 (s) where 
.
11) scale Nets without losses doubly loaded:
This configuration beyond comprising the cargo 2R and the resistance innerR 1 to the generator has
also optimal property of sensibility. Siccome the inner net is
LC then Pin(jw) = Pout(jw), follows
some 
where 
is the function
transducer and 
is the characteristic
function. By means of continuation analytics 
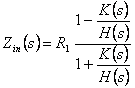is obtained that it can also be expressed in one of the two
following shapes:
,
.
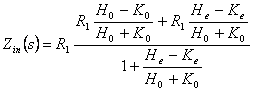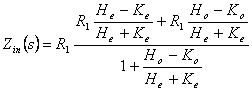12) Scalatura of the function trasduttore:
It has the scope to increase to the sensibility and the gain multiplying the function transducer for one opportune constant.
