Methods for the direct realization
1) Equations that describe the transmission parameters:
2) GIC:
(Generalized Impedance Converter)
Draft of a circuit that concurs to realize by means of various active members RC types of members is passed to you, some of which originates them. The circuit is the seguente:
Taking advantage of the fact that the potential difference
them to the clips of income of the operational one it is 0 and that
from the same ones it does not absorb current, the matrix of
transmission is obtained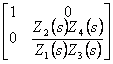 
.
3) GIN and its stiffness of income:
(Generalized Impedance Network)
It is obtained finishing the GIC with a stiffness
Z5(s), obtains a stiffness of 
income that expressed in terms of admittance is 
. By means of opportune chosen of the
stiffnesses they can be simulated is inductances that new members pass
to you.
4) Realization of inductances by means of GIN:
A GIN is used in which all the stiffnesses are of the
resistances except Z4 that is an
ability, follow some that the income stiffness is of inductive
type 
, using operational amplifiers of type matched
the effects of their not ideal parameters they come diminishes however
the realized inductance to you uses active members and therefore it
needs of a logon towards mass that it concurs some I only use it in
the filters pass-high where the inductances are placed
cross-sectionally. The sensibility to the elements of the GIN is ±1 turns the sensibility to the simulated inducer.
5) FDNR:
It is an element that introduces an admittance of 
income where D is one constant real positive that
measure in Farad-according to. The reason of the name is
obtained replacing s = jw , Y(j
w)=- w
2Dis hadin fact therefore a negative admittance and
employee from the frequency. Remembering that the admittance of
income of the GIN is 
a FDNR choosing Y 1
can be realized and Ythe 5 like admittances of remaining
condensers and admittances are conductances, obtain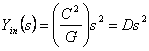 
. The FDNR can be only use you in the
realization of filters pass-low and pass-band in fact applying the
transformation of Bruton RLC " CRD consisting in a denormalizzazione of stiffness
with 
is had that the inductances series come
transformed in conductances and the condensers shunt in FDNR.
Moreover in order to concur a distance towards mass with the
continuous one, the condensers come bypassati from opportune
resistances. The realization of the pass-band with FDNR is more
complex in how much is better is not floating, obvious to the problem
using itself the cascade of a GIC, a GIN with stiffness Z(s) = s2D and an other GIC.
6) Leapfrog:
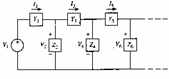The Leapfrog technique is not taken care to simulate the
behavior of some elements passes to you but it simulates by means of
of the tensions is the currents series that the tensions shunt of one
passive scale net
To which we can associate equazioni the and
therefore the diagram to blocks
 |
Therefore beginning from a simply or doubly loaded net RLC obtained through the tables the various blocks are characterized and it comes true them by means of integrators is simple that with summary losses, investers and.
In the case desires to come true a pass-band, the blocks to simulate are of type RLC or LC therefore can be realize with one whichever to you of the circuits that realize functions of 2° the order, the most adapted are the Tow-Thomas in how much the escape pass-band are available are inverting that not. In any case they are obtained of the sensibility next to those of the passive circuit of departure.
7) Filters to commutata ability:
In the integrated circuits the resistances of high value occupy space very, they can be realized in much little space and with more precision using one ability commutata according to the following outline
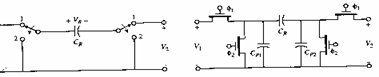
For which with j1 2 high andj bottom is had
while with j2 high and j1 basso 2Q = 0 therefore 
.
A resistore can be obtained negative using one various configuration of is made of the clock
is had 
in fact.
The realized resistances therefore can be used in order to realize inverting integrators, not inverting and with losses let alone filters Tow-Thomas and Leapfrog, a frequency of clock at least double must in any case be used regarding the maximum frequency present in marks them of income, in ottemperanza to the criterion of Nyquist, in practical it is at least 100 times greater. I use of the 4 MOSFET moreover concurs to diminish the effect of the parasitic abilities to the same ones when condensers of the order of the pF are wanted to be used with the aim to save space in the integrated circuit.