Approximation
1) Property of |N(jw)|2 associated to a function ration them N(s):
to) |N(jw)|2 are a relationship of polinomi
equal in w ci² are obtained
replacing jw = s in 
the and using 
b) replacing 
in |N(jw)|2 obtains the 
where N(-s) has the same poles
of reflected N(s) but regarding the origin, of it it derives that the
poles of T(s2) have symmetry
quadrantal that is are symmetrical is regarding the real axis that
regarding the imaginary axis. Such quadrantal symmetry is
possible single if the present poles and zeroes on the axis jw are of equal order.
2) massimamente flat Function:
Function is one |N(jw)|2 that it is massimamente flat
to ridosso of the origin, remembering that |N(jw)|2 are a relationship of polinomi
equal 
and confronting the last term obtained by
means of relationship with the expansion in series of Mac Laurin 
that for being massimamente flat must have the
greater number of null derivatives in the origin, of it it derives
that |N(jw)|2 massimamente flat can be
obtained if to the = b for the greater possible number of
coefficients.
3) Function of Butterworth:
It is proposed to us to realize one |N(jw)|2 massimamente flat therefore to = bthe i , of pass-low type therefore all the zeroes of transmission are to infinite and therefore all the b are zero like pure therefore to except that one of the maximum degree, are had:
where to the denominator there is w2n in how much |N(jw)|2 must be a relationship of
polinomi equal. The position of the poles is obtained that is
replacingjw = s w2= - s2 in |N(jw)|2 , are had 
, in particular:
to) for n uneven 
with k = 1, 3,
5, 4n-1
b) for n pari
with k = 0, 2, 4, 4n-2
only the poles that are found in the left semiplan
are stable, they are 
with 
e 
.
4) Polynomial di Butterworth:
It is the polynomial that one finds denominator of the
function of Butterworth 
where to0 = 1 since all the poles find on the
unitary circle and other coefficients are gained ricorsivamente by
means of 
the and are symmetrical that is
to0 = ton, to1 = ton-1, … .
5) Determination of the order of one function of Butterworth:
The order nB of a function of Butterworth is 
where 
ed 
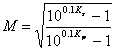being in the detailed lists that the passing band must be
comprised between 0 and wp and to introduce the maximum shunting line of Kp dB regarding the maximum
value while the stop band it is comprised between ws and ¥ and introduces one minimal
attenuation of Ks dB.
6) Denormalizzazione of frequency:
The function of standardized Butterworth previews a
frequency of cut to 1 rad/sec for which Kp is 3dB, for having a various attenuation to the same
frequency, the pulsation is necessary to carry out the
denormalizzazione of 
frequency 
being to which the function has the wished K attenuationp .
7) Polinomi di Chebyshev:
where i polinomi Cn(w) is defined by means of one of following:
to) 
beginning from
C1(w) = w
b) 
c) 
d) 
they are such that the module is fair-ripple in
passing band and monotonic decreasing in dark band. The
pulsations w which an
attenuation of â?"3dB corresponds to the pulsation of 1rad/s are
given from the relation 
.
The poles are gained replacing in |N(jw)|2 , they are situate
on one ellipse to you centered in the origin.
8) Determination of the order of one function of Chebyshev:
Order nC of a
function of Chebyshev is 
where ed
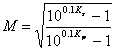being in the detailed lists that the passing band must be comprised
between 0 and wp and to introduce the maximum shunting line of Kp dB regarding the maximum value
while the stop band it is comprised between ws and ¥ and introduces one minimal
attenuation of Ks dB.
9) Function of inverse Chebyshev:
it introduces one characteristic fair-ripple in decreasing the dark and monotonic band in the passing band.
It is obtained replacing w with 1/w in 
the that is fair-ripple far away from the
pass-high origin but. The poles that turn out some are mutual
regarding those find to you for 
.
10) Determination of the order of the function of inverse Chebyshev:
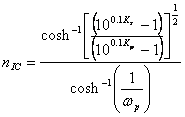
confronting this expression with that one found for the filter of Chebyshev it is had that they are equal on condition that is had
11) elliptic Filters:
They are also sayings filters of fair-ripple Cauer and
introduce one characteristic is in dark band that in passing band
moreover is characterizes from one greater slope to you in
correspondence of the frequency of cut regarding the other typology
of filters. The typical shape of a elliptic filter is 
where 
.
12) Transformation from pass-high pass-low:
If a pass-low function is defined in complex plan s = s jw by means of the 
transformation obtains a pass-high function in plan p = u
jv, imposing sinusoidale stationary state s = 0 it is obtained u = 0, 
. The effect on the function of N(s) net is that
the zeroes of transmission to the infinite come transform to you in zeroes
in the origin. The transformation can also be applied directly
to the elements of a net, cosicchè an inducer of K Henry transforms
in a condenser of 
Farad while a condenser of K
Farad transforms in an inducer of Henry.
13) Transformation from pass-low to pass-band:
If a pass-low function is defined in complex plan s = s jw by means of the 
transformation obtains a function pass-band in plan p = u
jv, imposing sinusoidale stationary state s = 0 it is obtained u = 0,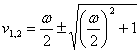 
. In particular the band of the pass-low one
becomes the band of the pass-band and every brace (v1,v2) is such that v1v2= 1.
The transformation pu² also to be directly applied to the
elements of one net putting in series to every inducer of K Henry one
ability to Farad and in parallel to every
ability to K Farad an inducer of Henry.
14) Realization of a filter pass-band of Broad-Band type:
It is a filter pass-band with a greater bandwidth regarding the standardized filter, denormalizzazione in frequency is obtained then operating one on the pass-low filter and executing the transformation pass-low® pass-band.
15) Realization of a filter eliminate-band:
It is necessary to apply the transformation to a pass-high filter
16) Approximation of tight band:
A filter pass-band is said to be to tight band if its
bandwidth is smaller of tenth regarding the center frequency a band
that is if 
. The denominator of the
function pass-band can itself directly be obtained in fattorizzata
shape in fact replacing 
nella obtains 
where s he is the
variable one regarding which the pass-low one is defined while p he is
the variable one regarding which the pass-band is defined.