The Transformed Z
1) Transformed bilateral Z :
it is an extension of the transformed one of Fourier, that it is obvious if the variable complex z in polar shape is placed:
it is observed in fact that functions like the step that for via of its discontinuity it does not admit transformed of Fourier, can be modified from the exponential r- n .
2) Criterion of convergence of the sequences to ended length :
They converge ovunque for 0 < |z| < ¥ , the ¥ value cannot be assumed if the inferior end of the summary one is negative while value 0 cannot be assumed if the advanced end of the summary one is positive.
3) Criterion of convergence of the sequences to monolatere skillful :
They converge to the outside of a circle of R beamx- .
4) Criterion of convergence of the sequences to monolatere left :
They converge to the outside of a circle of R beamx .
5) Antitrasformata Zeta :
where C is a situated closed arbitrary distance in the region of convergence of X(z) and that it encircles the origin.
In short 3 distinguished methods can be used in order to determine antitransformed z of one the sequence:
to) = sum residual of X(z)zn-1 in the inner poles to C where the
residual one of an order pole k is calculable through 
the .
b) long division which concurs to characterize a sequence of which is necessary but to know to write a shape sluice.
c) Decomposition in fratti simple, in short must be carried out a division before if the degree of the numerator is greater of the degree of the denominator, this last one goes decomposed in a product of monomials, which will be everyone the fratti denominator of the sum of n simple.
6) Regions of convergence of the transformed ones zeta ration them:
Skillful a monolatera sequence converges to the outside of cerchio a ;
a left monolatera sequence converges to the inside of cerchio a ;
a bilateral sequence converges to the outside of a circular ring.
7) Property of the transformed Z:
 |
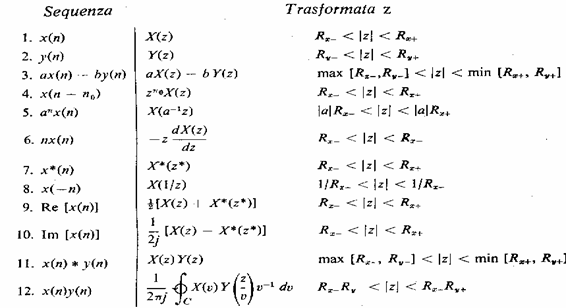8) Relation between the function of transfer and the answer in frequency :
they only coincide on the unitary circle.
9) Relation between a stable system and the convergence region:
It is had that a system is stable if the region of convergence of the transfer function comprises the unitary circle.