The transformed one of discreet Fourier
1) Representation in series of discreet Fourier of one periodic sequence:
The synthesis formula è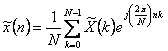 
while the
analysis formula è 
.
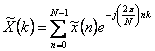Defining 
they they can it are
written 
e 
.
It is observed that the 
values in the
representation by means of the DFS of a periodic sequence, coincide
with the values of transformed z of a single period of 
taken in N points space to you uniform on the unitary
circle.
2) Property of the series of discreet Fourier :
 |
3) having Relation between a aperiodica sequence x(n) transformed X(z) and the periodic sequence whose coefficients of the DFS coincide with the equispaziati champions of X(z) in angle on the unitary circle :
that is the periodic sequence obtains gives it aperiodica sequence overlapping successive repetitions of this last, that involves that if the aperiodica sequence x(n) then is of ended duration inferior to N not there is aliasing.
4) Possible points of view for the transformed one of Fourier of sequences to ended duration :
to) one is associated to the sequence of ended duration long N periodic sequence of having N period only representation by means of the DFS.
b) the obtained periodic sequence sampling the transformed Z in N heads equispaziati at the unitary circle is identical to the coefficients of the DFS.
5) Sequence rectangle :
6) Transformed of discreet Fourier:
7) Property of the transformed one of discreet Fourier:
8) Execution of the circular translation of one sequence :
From a sequence x(n) pu² to obtain a periodic sequence if on this one translation of m champions is
executed, the sequence that is obtained is various from that the
sequence is obtained simply traslando x(n), images in fact to take a
period of the sequence, to close it like forming a cylinder, ruotarlo
of n steps and then reopening it.
9) Execution of the circular convoluzione:
The linear convoluzione consists in taking one of the two sequences, ribaltarla and traslarla and champion for champion to add the products, in the circular convoluzione instead must itself be imagined to take to a single period of both the sequences and to form two cylinders concentrate, to make to us to ruotare one regarding the other and to add the products. It is observed that this operation corresponds to multiply the discreet transformed ones of Fourier of two sequences, the antitransformed result gives back the convoluzione of the two sequences.
10) Calcolo of the linear convoluzione based on the transformed one of Fourier discreta:
9) Methods of calculation of the convoluzione of one sequence of ended duration (filter) with one sequence of infinite duration: Superimposition and sum
the infinite sequence comes subdivided in having sequences of L duration added of the zeroes in such way that adding the infinite obtained sequences riottiene the infinite sequence begins them. Executing the circular convoluzione of ciascuna of these sequences with the sequence of the filter, champions of the which M-1 obtain themselves of the sequences formed from L M-1 overlap themselves, therefore adding the segments he leaks is obtained to you marks leaked them.
Superimposition and extraction
the infinite sequence comes subdivided in sovrapponibili sequences of N length, the circular convoluzioni are estimated after which a part from ciascuna is eliminated of they and it turns out to you giuntano.