It marks them and systems to discreet time
1) It marks them to discreet time :
They are defined on with discreet of times, they can assume value whichever x(n), they are also calls sequences to you.
2) Energy of one sequence :
![]()
3) mathematical Description of a system :
Transformation is one univoca that map one sequence of income x(n) in one sequence of escape y(n) = T [ x(n) ]
4) invariant System to the translation :
If y(n) it is the answer to x(n) then y(n-k) it is the answer to x(n-k).
5) Sum of convoluzione :
![]()
6) stable System :
It is a system for which every limited income it provokes
a limited escape, systems LTI are stable if ![]()
7) linear Equation to the differences to constant coefficients :
![]()
8) System FIR:
An answer to the impulse of ended duration is a having
system, is described from an equation to the differences to
constant coefficients ![]() with N = 0.
with N = 0.
9) System IIR:
An answer to the impulse of infinite duration is a having
system, is described from an equation to the differences to constant
coefficients ![]() with N > 0.
with N > 0.
10) Transformed of Fourier of one sequence x(n) :
![]()
it is observed that in the case of a real sequence x(n), the real part of transformed its of Fourier is an equal function while the imaginary part is one uneven function.
11) Antitrasformata di Fourier of one sequence x(n) :
![]()
12) Aliasing of marks them championship :
It is introduced when the period of sampling is too much along for which the traslate retorts they come to sovrapporsi.
13) Relation between transformed of Fourier to transformed continuous time and of Fourier of one the sequence derived by means of sampling :
![]()
therefore the phantom of marks them championship is
periodic and coincides with the phantom of only marks them analogic in
(-p ,p) on condition that it is ![]() .
.
14) Formula of interpolation in order to reconstruct marks them to continuous time xto(t) to leave from its champions :
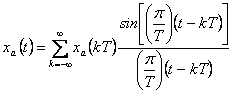
in order to reach to it part from the hypothesis that not is aliasing.
