It marks them and information
1) It marks them:
In tight sense physical largeness is one, real variable real function of usable or less like vehicle for the information.
2) It marks them sure:
It is characterized from an obtained famous course with mathematical functions, its graphical representation is called wave shape. To it some information in how much is not associated all the parameters is famous a priori.
3) It marks them aleatory:
Draft of marks them whose shape is not famous a priori and instead is tied to the information associated to marks them.
4) (t) Segnali faithful tox0:
It is marks them that respect to x is traslato0 and is multiplied for one constant g
that is 
.
5) Conditions of correct transfer:
to) the G generator it is represented with an ideal generator and one real constant inner stiffness and positive R
b) the utilizzatore U is represented with one real constant stiffness and positive Ru .
6) Conditions of ideal logon:
The exchanged instantaneous power must be maximum p(t), that is obtained for Zg(f) = Zu(f) = R.
7) It marks directed them and it marks reflected them:
8) It marks to climb them:
It is marks having them a codominio monodimensional.
9) It marks to regulate them in tor :
It exists ended the 
limit.
10) It marks them continuous in t0 :
It is marks them for which 
is had.
11) It marks them to continuous time:
The dominion is a continuous entirety.
12) It marks them quantizzato uniformemente:
It marks them says quantizzato uniform if the levels of quantization are all equidistanziati.
13) It marks them impulsive:
It is marks them that it is null to the outside of an interval of limited duration.
14) It marks them impulsive rectangular:
It extends from â?"T/2 a T/2 è 
.
15) It marks them impulsive triangular:
It extends from â?"T/2 a T/2 è 
con 
.
16) It marks them impulsive to raised cosine:
17) Define and to make an example of marks them bilateral:
It is marks them not null is for positive times you that
for times denied to you, an example is 
.
18) Define and to make an example of marks them monolatero right motive:
It is not null only for positive times you, an example is
marks them unilatero to exponential forfeiture 
.
MD (t)is hadx = x(t)u(t).
19) It marks them monolatero left antimotive:
It is not null for times only denied to you, has xMS(t) = x(t)u(-t).
20) Decomposition of marks them bilateral:
If it marks them is real, it can be decomposed in the sum
of the equal part 
e of the uneven part 
while if it is complex it can it are
decomposed in the sum of the hermitiana part 
and of the anti-hermitiana part 
.
21) It marks them to discreet time:
It is defined alone in the discreet moments {tn}.
22) Sequence:
It is marks them to discreet time with equispaziati
moments x(tn) = x(nTc), has 
.
23) generalized Function of Dirac:
It is the d of Dirac
defined from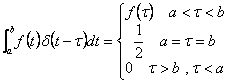 
it comes in approximate kind like limit of continuous functions.