It marks them sure in the dominion of the frequency
1) Transformed of Fourier:
2) Antitrasformata di Fourier:
that is it marks them x(t) is esprimibile by means of the sum of a number infinitely of complex harmonic functions andjwt of infinitesimal amplitude and distributed frequency f in continuous way on the real axis.
3) Phantom of marks them:
Draft of the transformed one of Fourier of marks them that is of X(F), its module is said amplitude phantom and is an equal function while its argument is said phase phantom and is one equal function.
4) Property of the transformed one of Fourier:
 |
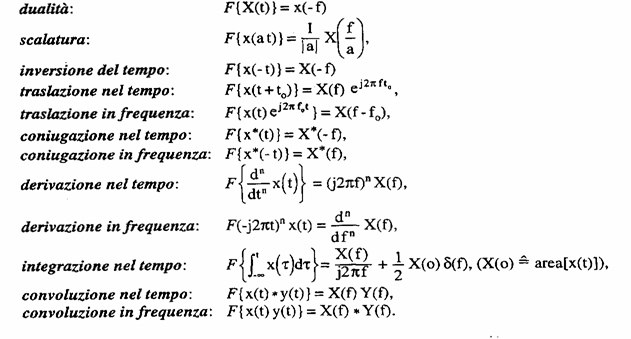5) F [ 1 ]:
d(f)
6) F [ sgn(t) ]:
7) F [ u(t) ]:
8) F [ rect(t/T) ]:
9) F [ sinc(t/T) ]:
10) Series of Fourier of marks them periodic continuous time:
being ck the
coefficients of Fourier, applying the transformed one of Fourier
obtains 
that is has a discreet phantom and all
the lines are spaced of one amount 
.
11) Sum of Poisson:
it is associated to marks them that it is obtained like
repetition with period T0 of
marks them generating x(t). Transformed its of Fourier is 
which in the case that marks them generating is an
impulse, it illustrates as to a comb of lines in the time a comb of
lines in the frequency corresponds.
12) Theorem of the sampling in the dominion of the frequency:
13) Transformed of Fourier of one sequence:
draft of one having function 
period
therefore enough to know the phantom between -p and p.
For real sequences the real part of the phantom is a function
pari while the imaginary part is one uneven function.
14) Property of the transformed one of Fourier of sequences:
 |
15) mutual Spectral density of energy:
It is the transformed one of Fourier of the intercorrelationship function, that is:
16) Spectral density of energy of marks them:
It is the transformed one of Fourier of the autocorrelationship function, that is:
for it marks them real is had that the spectral density of energy is real and equal.
17) It marks incorrelati them:
Draft of 2 marks them whose phantom is various from 0 in frequency intervals separates to you and therefore is null the mutual spectral density of energy.
18) It marks limited them in band closely:
The energy phantom is an equal real function for marks them real, extends between the maximum frequency fM and one minimal frequency fm , the band of marks them is therefore B = fM - fm .
19) It marks them in band base:
It is the typical one marks supplied them from a information source, its band is cos¬ allocata 0 £ fm £ fM, the single positive axle shaft is considered because for real and equal function marks them real the energy phantom is one.
20) It marks them in traslata band:
It is obtained elaborating marks them in band base to the aim to adapt it to trasmissivo means, its band is therefore allocata:
0 £ fm £ fc £ fM
21) It marks them in tightened traslata band:
It is marks them that it respects the 
condition.
22) It marks them in traslata band much grip:
It is marks them that it respects 
the
condition naturally includes 
the .
23) mutual Spectral density of power:
It is the transformed one of Fourier of the function of intercorrelationship of marks them of power, that is:
24) Spectral density of power of marks them:
It is the transformed one of Fourier of the function of autocorrelationship of marks them of power, that is:
