Ciclostazionari processes
1) ciclostazionario Process in tight sense:
It is a not stationary process for which a real number T
0 >0exists, said
period of ciclostazionarietà, such that the density of combined
probability verifies 
the where with xn' it means xn to time t1 T0 .
It is had that all the statistical moments of the ciclostazionario process are periodic functions with period T0 .
2) ciclostazionario Process broadly speaking:
It is a not stationary process for which the density of
probability of the 1° and 2° the order turns out periodic in the time
and consequently also valor medium statistical and the function of
autocorrelationship that therefore can be develops to you in series of
Fourier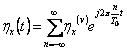 
where 
is the cyclical frequency.
3) cyclical medium Valor:
4) Function of cyclical autocorrelationship :
5) Spectral density of cyclical power:
Considering a single realization it is had
where XT(f,t0) is the transformed one of
Fourier of the restriction of the process x(t) to a T duration around
to t0 while is the cyclical frequency.
6) First relation of Wiener generalized Khinchine:
7) cicloergodico Process in tight sense:
It is a process for which all the temporal averages coincide with the medium correspondents statistics mediated on the period.
8) cicloergodico Process broadly speaking:
It is a process for which the temporal averages di1° and
2° order coincide with the medium correspondents statistics mediated
on the period, in particular 
e
is had.
9) Function of cyclical intercorrelationship :
In the case of two ciclostazionari processes broadly speaking with the same period T0 , ha
.
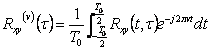10) Spectral density of intercrossed power cyclical:
11) Second relation of Wiener generalized Khinchine:
12) stationary and ciclostazionari Processes in vhf:
The autocorrelationship of the process in vhf x(t) can be
expressed in terms of the processes in null band medium base to valor
xp(t) in phase and xq(t) in quadrature, is had 
famous therefore that independently from i
processes xp(t) and xq(t) the process in vhf x(t) turns out
to be ciclostazionario broadly speaking with period 
.
The average temporal of the autocorrelationship function is 
which spectral density of potenza corresponds
one 
.
The two following particular cases can be had:
to) if the processes in band base are
stationary then also x(t) are stationary and 
e 
is had
therefore the autocorrelationship is reduced to 
and therefore the spectral density of power
is 
.
It is observed that for t = 0 it is obtained for the density of power 
and for the variances 
therefore xp and xq they are orthogonal processes and their
density of combined probability is the single product of the density
of probability, in the case they are Gaussian have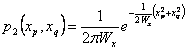 
and being 
and 
co-ordinate a change of with Jacobiano J = r that
it gives back , saturating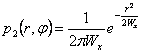 
regarding j
ottiene that is 
one can be made density of probability of
Rayleigh type while saturating respect to r 
is
found that is a density of probability of uniform type therefore the
brace of variable is statistically independent. Moreover the
density of probability of the process instantaneous power 
is exponential 
.
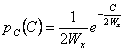b) if the processes in band base are
ciclostazionari and supposing for semplicità xq(t)=0, the function of autocorrelationship are 
whose medium autocorrelationship is 
which the spectral density of power 
therefore to the phantom corresponds of marks them in vhf corresponds
also the cyclical phantoms of marks them in band base.
13) Property statistics of the harmonic oscillation in presence of Gaussian noise:
The expression of the process in vhf in presence of pure a
harmonic oscillation is 
con 
, comes moreover defined the
autocorrelationship 
and the function of
pseudocorrelation 
that concurs to write
the autocorrelationship of x(t) in the shape 
that turns out to be periodic with 
period
therefore the process is ciclostazionario broadly speaking as he was
expectable for the presence of the harmonic member.
The medium autocorrelationship is 
whose transformed of Fourier it is the spectral density of power and
evidences the superimposition between the phantom of the harmonic
oscillation and the phantom of the noise in vhf. If the
processes in band base are Gaussian, the density of combined
probability 
dove 
is had, through the change of coordinated 
, 
having Jacobiano J =
r is reached the shape
that, saturated regarding j returns 
while saturated respect to r it gives 
with 
, finally the density
of probability of the process instantaneous power is 
.
14) Phantom of power of marks them in band base:
It is assumed marks them of power in band 
base where tok it
is a stationary discreet process broadly speaking with statistics hTo , RTo , s2To while q(t) it is marks them of transformed energy with of
Fourier Sq(f) and energy 
the medium value of x(t) is 
and is therefore periodic with pure Tperiod s like the
autocorrelationship function 
from which integrating on Ts the cyclical autocorrelationship with v=0 is
obtained that with a variable change of filler to the shape 
(…where andq(t) it is
the autocorrelationship of marks them of energy q(t)) that estimated
for t= 0 and replacing 
it supplies the power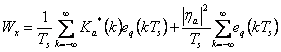 
while the spectral density of power is obtained transforming according
to Fourier Rx(t), obtains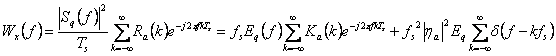 
that is one phantom to lines overlapped to one distributed phantom.
It is observed that if the process {tok}è white man or if q(t) is to
orthogonal retorts, the power of the ciclostazionario process x(t) is
equal to the relationship between the energy of the shape of
determinist wave and the T periods that is 
.
15) It marks them in generalized band base:
The shape more general than marks them in band base x(t)
is obtained like combination of M shapes of extracted
energyx j ciascuna with a priori probability P and with T cadences , is had 
that is, on it comes defined the medium symbol 
that in the case marks them comes represents to you
in the space of marks them coincides with the barycentre of the
constellation of the symbols. The phantom that of it turns out
is given from the superimposition of a continuous phantom and of a
distributed phantom, this last one can be interpreted like phantom of
power of the shape of periodic wave 
that
coincides with the expected value of x(t) that is 
and that being periodic it can be decomposed in
series of Fourier 
where Sto(f) is the transformed one of
Fourier of the medium symbol 
whose module
picture gives back the spectral density of power to lines 
and therefore famous that the phantom of marks them
periodic it is discreet and it possesses entire multiple lines of the
symbol frequency.
16) Phantom of two power marks them in band base:
It marks them sum of two marks them in band base is 
which cyclical autocorrelationship with
ciclicità v=0 
corresponds that
estimated in t = 0 gives
back the power 
where the intercrossed
correlation is worth 
quindi 
.
Transforming according to Fourier the cyclical
autocorrelationship 
dove 
, 
, 
is obtained, replacing last the three expressions in
the Wz obtains a relation
that in the case of processes white men with hTo= 0 e sTo2 = 1 is reduced to 
the
from which integrating the is obtained 
potenza.
17) geometric Representation of the aleatory processes
A medium aleatory process x(t) to valor null can
be represented in an ended interval 
through the
development in series 
where yk(t) is with
of n ortonormali functions in the 
interval
while {ck} is a discreet
aleatory process to valor medium nulo, if this last one introduces 
correlation the development is said in series of
Karhunen-Loeve.
With the aim to find an equation that it concurs to
determine ykthe (t) it calculates the intercorrelationship between the
processes x(t) and ck , has 
of the rest for i coefficients ck can be written the relation 
, replacing it in the calculation of the
intercorrelationship has 
uguagliando the two
found expressions obtains a system of equations to the autofunzioni 
which they must satisfy the
autofunzioni of base yk(t).
The equality is an equality
between processes and must verify the quadratic convergence in average 
however in the case of development KL has 
that is demonstrated to be necessary
condition and sufficient affinchè the quadratic convergence in
average is respected. Through the substitutions
, 
, 
, 
, 
the system of equations comes standardized that is led back to the interval [ - 1, 1 ], is had:
where the ck is orthogonal functions in
the interval [ - 1.1 ].
The two following examples of application are made:
to) Representation of noise white man in an ended interval
The function of autocorrelationship of x(t) is 
with 
being Nx the spectral density of the
bilateral process, replacing obtains the system of equations 
that it has as solution of the said functions
spheroidal crushed.
b) Representation of noise white man of infinite duration
The function of autocorrelationship of x(t) is with being Nx the spectral density of the
bilateral process, but in this case it is made to stretch to infinite
the integration interval, replacing in 
the
and taking advantage of the relation 
N
xis obtained q k= and therefore process {ck} turns out stationary broadly
speaking, it finds moreover that the relation 
is verified and therefore the quadratic convergence
in average is had.
