Reticular vibrations

1) Group velocity:

Draft of the derivative of the angular pulsation w regarding the carrier of wave k, .

 

2) propagantesi Characteristics of an elastic wave in one chain formed from equal atoms:

It is supposed upgrades them of elastic type where x are the movement therefore the acting force are .

We consider a linear atom chain you mail at a distance to between of they, the force that acts on the atom in the position s due to the atom in the position s p is proporziona them through constant C_p to the difference of their movements u_s and u_{s p} regarding the positions of equilibrio .

Considering as origin the beginning of the chain and searching solutions of sinusoidale type and replacing in the equation differentiates them it has and dividend for obtains where the interaction with atoms to equal right to the interaction with atoms has been considered on the left. If it is limited to us to the interaction with single first neighbors therefore p = 1 and the term within parenthesis like a breast is written, the relation of dispersion is obtained.

 

3) 1ª zone of Brillouin:

Writing the relationship between the value of the movement in a point u_{s p 1} and the value of the movement in the previous point u_{s p} one finds and^ika that it is a periodic amount with period 2p of to which they interest us is positive values you that values denied to you why the waves can propagar are to right that on the left therefore -p £ ka £ p being to the distance between 2 atoms of the chain. is had that represents the first zone of Brillouin.

 

4) Characteristics of the dispersion relation:

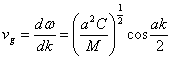We have seen comes obtained considering the single interaction with the first neighbors in the case of a chain formed from equal atoms, ha from which pu² to gain the group velocity from which famous that in correspondence to the edge of zone has v_g= 0 and therefore we are in presence of a standing wave.

 

5) Relationship between v_g , v_s and the relation of dispersion:

the group velocity pu² to gain itself from the relation of 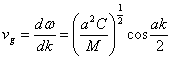dispersion. For k small that is in the acoustic band it is had that the diagram of the dispersion relation is assimilable to one straight and therefore

 

6) propagantesi Characteristics of an elastic wave in one chain formed from 2 having atoms various masses:

It is supposed of having a linear chain constituted from an atom alternation with mass M₁ and of atoms with mass M₂ , the interaction of the atom with mass M₁ place in position 2s 1 with the first neighbors is given from the equation differenziale:

Analogous the interaction of the atom with mass M₂ place in position 2s with the first neighbors is given from the equation:

Draft of 2 equations differs them for which we try solutions in the shape of two having sinusoidi same pulsation but various amplitudes for having atoms various masses that is e which replaced in the equations differentiates them damage a system in incognito x and h which have single solution if the determining one is cancelled that is if from which it is gained that for every w 2 various values of k exist and analogous for every k exists 2 various values of w in particular the solution with sign goes to to describe w to the higher correspondents to the optical branch that assumes the maximum value for k=0 and the minimal value on the zone edges. The solution with the â " it characterizes instead the acoustic branch that is much similar to the curve of dispersion found in the case of one identical atom chain. Between the 2 branches is one forbidden branch.

 

7) First zone of Brillouin in the case of one chain formed from 2 having atoms various masses:

Writing the relationship between the value of the movement in a point u_{s p 2} and the value of the having movement in the previous point the same mass u_{s p} finds and^ik2a that it is a periodic amount with period 2p of to which they interest us is positive values you that values denied to you why the waves can propagar are to right that on the left therefore -p £ 2ka £ p being 2a the distance between 2 having atoms of the chain the same mass, in formulas has .

 

8) Characteristic of the optical ways:

Placing k=0 in the equation of the optical branch and replacing in it the equations of the system in x and h is found therefore the atoms vibrates in phase opposition.

 

9) Characteristic of the acoustic ways:

Placing k=0 in the equation of the acoustic branch and replacing in it the equations of the system in x and h is foundx = h therefore the atoms vibrates in phase.

 

10) Conditions to the contour of Karmann:

The champion is limited therefore must suppose to join the ends and therefore to demand that the wave assumes the same value is to the beginning of the chain for s=0 that to the end for s=L. is had which is only verified for therefore has one quantization on the k. In order to find the number n of the k you concur yourself in 1ª the zone enough to multiply the density of states in k to unit of length for the length of 1ª the zone, has equal that is to the atom number therefore the k are quantizzati but they approximate a continuous one. Analogous the amplitude of 1ª the zone can be divided for the distance between two k is concurred .