Thermal property of the insulators
1) thermal Ability to constant volume and its diagram classic:
It is defined like the partial derivative of the inner
energy and regarding the T temperature to constant volume 
. For the classic mechanics, the inner atom energy
every is estimated associating to everyone of its 6 degrees of freedom
(3 vibrazionali and 3 traslazionali) a 
energy
therefore considering an atom size the inner energy is 
and therefore 
constant therefore
with the temperature. Confronting it with the surveys it
experiences them obtains that this representation substantially is
corrected to high temperatures while to lowlands, the thermal ability
stretches ago to 0 and like T3 , in
order to explain such behavior is necessary to consider the inner
energy due to the single ones fononi, for everyone of they has 
therefore the energy total is 
dove 
(where m = the 0 in how much fononi are particles lacking in mass)
are the function of occupation of Bose that describes the n° of fononi
that to one given temperature they possess the pulsation wk but we have
inasmuch as the k contained in 1ª the zone they approximate a
continuous one therefore can be replaced the summary one with an
integral
. A difficulty of such integral
resides in the D(w), it can
experimentally be obtained and the deliberate integral numerically or
the approximations of Einstein and Debye are used.
2) N° of occupation of the fononi:
The fononi they are of bosoni therefore the number of the
fononi that to one given to temperature posseggono one given energy it
is given from statistics of Bose Einstein 
. A consideration important to
make that it is to the base of the hypothesis of Debye is that when T®0 is had that the number of the
fononi is elevated for w small
and therefore from the dispersion relation, for k small.
3) linear Density of states in k:
We have gained from the conditions to the contour of
Karmann that the distance between two k you concur yourself
consecutive is 
, in order to find the density w(k)
of the k enough to make of the mutual one obtaining 
.
4) Hypothesis of Einstein:
Einstein proposes a following density of states in w of 
type,
that is that every fonone it possesses the same pulsation w=weinstein=wand therefore considering a N size of
fononi, everyone of which (if it is worth the law of Hooke) possesses
3 independent ways of vibration (2 cross-sectional ones and a
longitudinale) 
is had from which 
from it is had looks at that for T®¥ the exponential can be
developed in series and C is foundv®3Nk=3R while for T®0 the exponential to the denominator
diverges and therefore Cv®0 like a exponential and not like T3 that is the value experiences them,
this has had to the bad approximation of the D(w) that however for high temperatures it
is from preferring to the approximation of Debye.
5) Expression of the density of states in w in the case of one linear chain:
Observing the dispersion curve it is necessary to put in
relation the density of states in w D(w) with the density
of states in k 
has 
allora 
. Replacing the expression of
the Vg that one obtains from the
dispersion relation it sees that the D(w) diverges to ¥ in
correspondence to the vertical asymptote w = wmax . With the approximation of Debye the D(is found thatw) is constant until to the value wD .
6) Hypothesis of Debye:
Debye observes from the function of occupation of Bose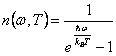 
that to low temperatures (..sono the temperatures
that interest because for they the classic ability is mistaken) are
many fononi with k small, but in these regions the dispersion curve
can be approximated with 2 straight tangents to the limit for k®0. The effects of this
approximation are 2:
to) Remembering that 
has 
constant and therefore pu²
to be carried outside from the integral of Cv .
b) They change to the ends of integration in how much the straight tangent meets vertical passing for the edge of zone for wD > wmax ha wD = the 1,57 wmax .
Carrying out the calculations C v0®like T 3is found .
7) superficial Density of states in k:
It is 
, is obtained in analogous
way to the unidimensionale case.
8) Considerations on the approximation of Debye in the bidimensional case:
The D(is writtenw) considering of the lines to w constant, obtains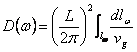 
, in
order to simplify it according to Debye v are placedg = vs and door outside from the integral and moreover
approximates the curve of dispersion with a circle of beam k therefore 
that replaced in the integral concurs to
calculate the inner energy. You notice yourself that the
advanced end of the integral is wthe D that is obtained uguagliando the
number of fononi to the product between the density of fononi to unit
of surface for the area of the circumference of Debye. As result
obtains that the density of states is crescent in w until to w the correspondent to the edge of the 1ª zone
dopodichè it decreases until being worth 0 in correspondence to the
value of the beam of the approximating circumference.
9) volumica Density of states in k:
It is 
, is obtained in analogous
way to the unidimensionale case.
10) Considerations on the approximation of Debye in the three-dimensional case:
The D(is writtenw) considering the superficial ones to w constant, obtains 
, in order to simplify it according to Debye v are
placedg = vs and door outside from the integral and
moreover approximates the curve of dispersion with a sphere of beam k
therefore 
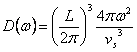that replaced in the integral concurs
to calculate the inner energy. You notice yourself that the
advanced end of the integral is wthe D that is obtained uguagliando the
number of fononi to the product between the density of fononi to
volume unit and the volume of the sphere of Debye. As result
obtains that the density of states is crescent quadratic in w.
11) Temperature of Debye:
It is a measure of the force of the tie that characterizes
the reticulum, greater is the temperature of Debye, greater is the
force of the tie. It is obtained from the 
relation, is therefore the temperature that corresponds towthe D .
12) Causes of the thermal expansion of the solid ones:
The forces of interaction between 2 atoms are not
described from a harmonic oscillator therefore from a 
parabola since to it a linear 
corresponds for which therefore it is worth the
superimposition of the effects but from a more complex and above all
asymmetric function, therefore an atom that to continuation of the
somministrazione of heat oscillates around to the equilibrium
position, ago in asymmetric way in the 2 directions and therefore the
medium movement is not null and therefore the linear chain is dilated.
13) Coefficient of thermal conductivity K:
It is the coefficient of K proportionality between the
amount of Q heat that flows in a material and the gradient of
temperature in present it, has 
. In order
to gain the value of K it is observed that the amount of heat
transported from n having particles ciascuna thermal ability c is 
, of the 
rest where t the time is the time of relaxation
that is that elapses between 2 hits happened to you, moreover
considering a unitary surface is had that in the time unit it is
crossed from n|vx| fononi altogether in the two backs therefore 
is had where the isotropia has been supposed
therefore 
. Being l=vt the free medium way and C=nc the thermal ability
total of the system is had 
therefore 
.
14) Free medium way of the fononi:
It is the medium distance that they cover between a collision and the successive one, is function of the following causes:
to) Presence in the various atom reticulum which isotopes or impurità
b) physical Limitatezza of the reticulum
c) Collision between fononi
15) Laws of conservation in a collision between fononi:
Law of
conservation of nearly the moment
Law of conservation of the energy
Attention, is not necessary that the number of fononi conserves.
16) Typology of hits between fononi and free medium way:
When 2 fononi they are come to find in the same region spaces them, a collision is had in which it must be conserved the amount of energy and the impulse, the 2 following types of collision can be verified:
to) normal Collision it is had when the k turning out from the vectorial sum of the k of fononi the incidents the fonone is contained in 1ª the turning out zone therefore is still in the direction of the motion and contributes to the thermal conduction.
b) Umklapp Collision is had when the k turning out from the vectorial sum of the
k of fononi the incidents it exits from 1ª the zone but
sottraendogli a carrier of the mutual reticulum obtains a fonone with
a k such from opporsi to the motion. The fononi useful they are
those that they have k next to the edge of 1ª the zone, their number
linearly grows with the temperature in fact 
therefore the thermal conductivity descresce linearly with the
temperature.
17) Imperfections and free medium way:
The effect of the imperfections has place when the medium free way which had to the processes of Umklapp is comparable to the physical dimensions of the crystal, therefore the free medium way is only constant with the temperature.
18) Value of the thermal conductivity in function of the temperature for an insulator:
Variation is necessary to analyze of coefficient of
conductivity thermal 
with temperature, it has
that to high temperatures process predominates of
Umklapp in how much fononi effective grows to to grow of temperature,
to temperatures next to temperature of Debye qD number of fononi effective
decreases like exponential negative, while if T®0 the number of fononi effective
stretches to the zero and therefore free medium way is constant in how
much tax from the imperfections and the dimensions of the crystal that
is constant, and dominates therefore thermal ability C which pushes
the thermal conductivity to zero like T3.
19) Typology of usable probes in order to analyze the characteristics of the fononi:
to) the electron which not neutral being has the problem and therefore it is valid only for one superficial analysis of the material.
b) the electromagnetic cancellation and in particular i beams x.
c) the neutrons which react weakly to the magnetic fields but are difficult to generate and to stop.