Property of the metals

1) Model of Drude:

The atoms of the metal are all making use, have therefore a single electron on the more external layer, it weakly are attracted from the ambient nucleus therefore already to temperature go away from the origin atom, that happens for all atoms and it is come therefore to create an electron cloud which facilitates is the thermal conductions that electrical workers and act as from adhesive for the crystalline reticulum. The model is in a position to explaining the linearity of the law of Ohm in how much supports that the electron accelerated from an external electric field continuously comes to hit against the Ionian ones of the reticulum and pertando moves with a speed of drift v_d . With this model electrical worker finds itself for the conductivity.

 

2) Law of Wiedemann - Franz:

in fact 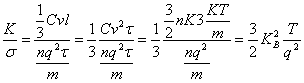is had where being has been replaced the energy classically associated to every fonone while v obtain from the equality between the thermal energy and the kinetic energy .

It is observed that there is linearity in the comparisons of the temperature and that it is valid for a whichever material in how much of is independent the number of Lorenz . Draft of a law that comes developed in terms of times of relaxation and that it is found experimentally and therefore supports the model of Drude.

 

3) Problematic not explicable with the model of Drude:

to)       the thermal ability they of the metals based on the model of Drude experiments would have to be advanced of 50% to the thermal ability to the insulators in fact in the metals beyond to the fononico contribution 3R has also the electronic contribution . That puts in crisis the model of Drude in fact for an insulator had while for the substantially identical metals is found experimentally therefore unless to low temperatures where a linear and not cubical course has itself.

b)       the Hall effect from which desume that the bearers of load not necessarily they are electrons.

 

4) Hall Effect:

A field is applied and_x to one conductor covered from current, dipped in a field of magnetic induction B directed along z, the charges in motion are subject to the force of Lorentz that it pushes to them towards a sidewall of the conductor, this separation of the charges give to place to an electric field who works in opposite sense, to regimen obtain therefore a balance between the two effetti from which the constant of Hall is obtained .

 

5) Model of the gas of Firm of free electrons:

The metal is seen like one scato it empty (deprives of reticulum) to the inside of which there are the fermions that do not have some interaction between of they, this is the reason for which it is spoken about gas. For saying gas the single kinetic energy is applied to the equation of Schroedinger considering in the Hamitoniana therefore the curve of and according to k parabola is one. In the unidimensionale case is had, if of it they try solutions in the shape of complex esponenziali imposing then that y(x) assumes equal values to the two extremities, in agreement with the conditions of Karmann has the quantization of the k, in fact they are valid only the k such that . Moreover be a matter of fermions you they can be two of they with the same one k purchè have spin opposite.

 

6) Considerations on the impulse of the free electron:

The theory of schroedinger assigns to the impulse the operator, it must verify the relation with is obtained .

 

7) Energy of Firm:

Draft of the energy correspondent to the carrier k of the last inserted electron. In order to gain it it is observed that the energy in the gas case of Firm is and moreover the value of k obtains imposing that to the beginning and the end of the chain the function assumes the same value and therefore as for the conditions of Karmann is found but for the symmetry of the parabola it is had that on every quantico level n 4 are offered of n the electrons therefore and of the L=Na rest where L is the length of the linear chain and to the separation between an atom and the successive one therefore it has from which ottiene .

 

8) Function of Firm distribution of Dirac:

It is worth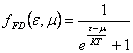 where m are upgrade them chemical that is equal to the energy of Firm only to 0K.

 

9) As to calculate it upgrades them chemical:

If you notice N and D(and) enough imposing .

 

10) Point of Firm:

It is a point of the axis of the k that it separates the full states from the empty states, in clean way to the temperature 0K and in less gradually defined way with increasing of the temperature.

11) Density of D(statesand) in the unidimensionale case:

It characterizes the number of electronic states for unitary interval of energy. It is estimated observing that to every quantico number n there are 4 states of energy available (for the symmetry of the parabola and the principle of exclusion of Pauli) therefore but being 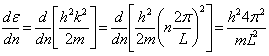quindi where in the last one has been replaced. After all therefore the diagram of D(and) according to and is a decreasing exponential , which multiplied for the function of distribution of firm-Dirac it says to us that under the exponential the states are only occupied for and < and_{the F} .

 

12) Circumference of Firm:

It is a circumference of the plan of the k that it separates the full states from the empty states, in clean way to the temperature 0K and in less gradually defined way with increasing of the temperature.

13) density and Sphere Firm of D(statesand) in the three-dimensional case:

It is a sphere in the space of the k that it separates the full states from the empty states, in clean way to the temperature 0K and in less gradually defined way with increasing of the temperature. Reasoning as in the unidimensionale case is found, draft of a root under which for and < and_F there are the occupied states.

 

14) Explanation in terms of gas of Firm of the equality between the thermal ability to the insulators and the metals:

In short the dilemma is that it is not understood like, being to us many electrons, they does not contribute to store energy, the explanation of that in term of the gas of Firm is that the electrons are very cram to you and regulated from the principle of Pauli therefore those to you to smaller energy cannot exchange energy because they do not have to disposition be free on which to dislocate itself with the little energy that comes to it supplied for thermal way. The percentage of electrons that can acquire energy KT is therefore the electron number that can acquire energy is and the energy total is therefore and from it the thermal ability is only gained draft of an inferior value of a cent regarding the thermal ability due to the fononi in how much T⁴ _F @10K.

We are therefore in a position to interpreting the course experiences them of the thermal ability to the metals asserting that to low temperatures the linear course which had prevails to electrons while to high temperatures the cubical course which had prevails to the fononi.

 

15) Explanation in terms of Firm gases of of the conductivity electrical worker:

Ç$⪠the law of Ohm in local shape is , in order to gain v_d applies to an electric field and, the force that acts on the electron is and for 2ª the law of the dynamics from which it looks at that is constant and therefore there is a uniform rectilinear motion in the space of the k, the presence of the imperfections is in a position to maintaining traslata the sphere firm after is moved in the time dt of the amount , then has from which and therefore the conductivity electrical worker is .