Diffraction of crystals and mutual reticulum
1) Condition of Bragg:
It is the condition for imposing to the wavelength of a cancellation incident with an angle q regarding axis x so that it can give place to constructive interference if sended against of the reticular plans separates from the distance d. the condizione to you
![]()
it is obtained characterizing immediately below the reticular plan, designing the beam that reflects on it and estimating the optical length in more regarding the reflection on the overhanging plan. Affinchè the two beams are in phase are necessary that such difference of distance is a multiple n of the wavelength l.
2) Calcolo di Laue for the amplitude of the diffuse wave:
Draft of a calculation that comes introduced in order to limit the error of base of the calculation of Bragg, that is considering the reticular plans like of the perfectly reflecting mirrors and therefore.
One of the points of the reticulum like origin is
considered Or, a point situated at a distance r from it comes invested from a flat wave ![]() that we will always consider to time t = 0. In r
that we will always consider to time t = 0. In r ![]() is had
but this point becomes source of secondary spherical waves for which
the amplitude of the cancellation on the detector place at a distance
r from r and R from the origin
it is
is had
but this point becomes source of secondary spherical waves for which
the amplitude of the cancellation on the detector place at a distance
r from r and R from the origin
it is ![]() where kr they are the modules because in
a spherical wave the two carriers are always parallels.
where kr they are the modules because in
a spherical wave the two carriers are always parallels.
We write r in function of the others grandezze ![]() and therefore ha
and therefore ha 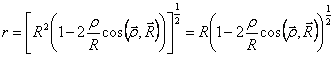 where r< < R in how much the
crystal has infinitesimal dimensions, then developing in series of
Taylor has
where r< < R in how much the
crystal has infinitesimal dimensions, then developing in series of
Taylor has ![]() that replaced in the exponential
gives
that replaced in the exponential
gives ![]() to the term andikR can be neglected in how much
constant on all the volume while
to the term andikR can be neglected in how much
constant on all the volume while ![]() being
being ![]() the carrier in the having direction that the
origin with the detector combines and as module k has
the carrier in the having direction that the
origin with the detector combines and as module k has ![]() where Dk it is
the carrier of scattering.
where Dk it is
the carrier of scattering.
Naturally the detector the contributions of the other
points of the reticulum reach 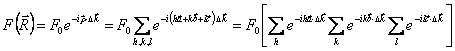 also.
also.
If as an example in the reticulum there are M atoms and we
consider the first only summary one is had: 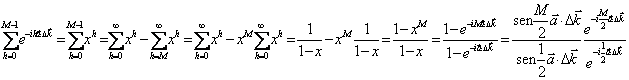 where
I have collected the exponential with the half of the exponent.
where
I have collected the exponential with the half of the exponent.
It comes but found the module picture of this largeness  the maximum of which it is obtained cancelling
the denominator that is for
the maximum of which it is obtained cancelling
the denominator that is for ![]() and therefore
and therefore ![]() the where q it is an entire one.
the where q it is an entire one.
Analogous for the summary others 2 trovano ![]()
![]() .
.
This calculation is but still imperfect in how much it does not hold account of the scattering multiple.
3) Conditions of Laue for the maximum diffraction:
They are gained from the previous calculation of Laue:
![]()
![]()
![]()
where q, r, s is of the entire numbers.
4) Carriers of translation of the mutual reticulum:



where the denominator represents the volume of the cell of the crystalline reticulum.
Their expression has been constructed so that one whichever they linear combination satisfies the equations of Laue for the maximum diffraction.
5) Condition of diffraction:
Diffraction is had according to Laue when the carrier of
scattering ![]() turns out to be equal to one whichever of
the G carriers of the mutual reticulum that is
turns out to be equal to one whichever of
the G carriers of the mutual reticulum that is ![]() ,
does not have to be demonstrated null in how much the carriers of
translation of the mutual reticulum
,
does not have to be demonstrated null in how much the carriers of
translation of the mutual reticulum ![]()
![]() ,
,![]() has been constructed just so as to to
satisfy the equations of Laue. This law can also be expressed in
various shape in fact
has been constructed just so as to to
satisfy the equations of Laue. This law can also be expressed in
various shape in fact ![]() allora
allora ![]() , elevating to the square
, elevating to the square ![]() is had
but be a matter itself of scattering elastic it is had k'= k and therefore the equation
assumes the shape
is had
but be a matter itself of scattering elastic it is had k'= k and therefore the equation
assumes the shape  that is satisfied if k it
finishes on a normal plan to
that is satisfied if k it
finishes on a normal plan to ![]() in the means point
of
in the means point
of ![]() .
.
6) Relation between mutual reticulum and crystalline reticulum:
Every carrier of the mutual reticulum is orthogonal to a plan of the crystalline reticulum.
We consider the plan that intersects the aces of the
crystalline reticulum in the points ![]() ,
, ![]() ,
, ![]() to it belong the carriers
to it belong the carriers ![]() e
e ![]() . It is demonstrated that
their vectorial product with a generic carrier
. It is demonstrated that
their vectorial product with a generic carrier ![]() is worth 0, obtain 3 equations that they are satisfied for
is worth 0, obtain 3 equations that they are satisfied for ![]() ,
, ![]() ,
, ![]() in which
looks at that the coefficients of G correspond to the indices of
Miller of the crystalline reticulum.
in which
looks at that the coefficients of G correspond to the indices of
Miller of the crystalline reticulum.
7) Distance between two reticular plans:
It is given from the relation  where h, k, l they are the indices of Miller of the plan to which G he
is orthogonal. From this relation one deduces that to every
point of the mutual reticulum possible reflection of the crystalline
reticulum corresponds one.
where h, k, l they are the indices of Miller of the plan to which G he
is orthogonal. From this relation one deduces that to every
point of the mutual reticulum possible reflection of the crystalline
reticulum corresponds one.
8) Relations between the laws of Bragg and that one of Laue:
The two laws are equivalents in fact 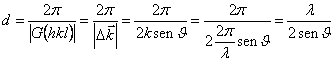 and therefore
and therefore ![]() is had that is just the condition
of Bragg.
is had that is just the condition
of Bragg.
9) First zone of Brillouin:
Draft of the cell of Wigner Seitz constructed on the mutual reticulum.
10) Sphere of Ewald:
Being ![]() allora
allora ![]() therefore designing to a carrier k that you finish in
to a whichever point of the mutual reticulum and imagining to make it
to ruotare so as to to create a circle or a sphere, if this last one a
diffratto beam intersects an other point of the mutual reticulum, you
form yourself, the found
therefore designing to a carrier k that you finish in
to a whichever point of the mutual reticulum and imagining to make it
to ruotare so as to to create a circle or a sphere, if this last one a
diffratto beam intersects an other point of the mutual reticulum, you
form yourself, the found ![]() carrier is orthogonal to
the plan of the crystalline reticulum regarding which there is
reflection.
carrier is orthogonal to
the plan of the crystalline reticulum regarding which there is
reflection.
11) Factor of geometric structure:
The theory of Laue is corrected in the every case
reticular point is formed from a single atom but if the atoms are more
than one, a factor of geometric structure will have to be considered
that account of the position of these atoms to the inside of the
unitary cell holds this factor of correction is worth  where fj it is
the shape factor and it is a measure of the power of scattering of the
atom j-esimo in the unitary cell.
where fj it is
the shape factor and it is a measure of the power of scattering of the
atom j-esimo in the unitary cell.
