Lines of transmission

1) Connection to unifilare :

It comes used a single conductor while for the return the earth is used.

 

2) Circuit to distributed constants :

It is spoken about circuit to distributed constants when the relationship between the length of the line and the speed of the light is approximately of the same order of magnitude of the meaningful considered temporal variations. If instead the temporal variations they are much more disc of a valve, is sufficient the analysis through the circuit to concentrated constants.

 

3) Equations generate them of the lines :

Assembling the longitudinal stiffnesses in an only stiffness to length unit and the cross-sectional admittances in an only admittance to unit of length from cui can be written , and analogous from which .

 

4) Solution of the equations generates them of the lines :

Deriving respect from x the obtains , placing the solution of this equation is . Analogous deriving respect to x the obtains whose solution is which can according to also be written simply replacing in the , has infatti in which uguagliando the coefficients of the esponenziali it accredits has and analogous it is found

where Z₀ is said characteristic stiffness of the line. Therefore the solutions of the equations of the lines are:

 

5) Constant of propagation of the line :

 

6) characteristic Stiffness :

 

7) adapted Line:

Draft of a line sluice on an equal stiffness to its characteristic stiffness, the condition of closing on the cargo is quindi replacing in it the equations e obtains and therefore , taking advantage of this last one (…than substantially indicates the absence of the regressive wave) and the condition of closing to the income on the generator, has , after all the equations in the case of line adapted on the cargo is e . Analogous if generator V_g comes place to the end of the line and the cargo Z₀ to the beginning, it is had that and therefore has only the regressive wave.

 

8) Stiffness in the case of adapted line:

When the line is adapted the stiffness that is looked at towards the cargo in a whichever point of the same line is always equal to the characteristic stiffness. It is demonstrated observing that in the case of progressive wave the 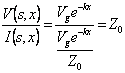relationship is constant, if instead we consider the line adapted in income has â?"Z₀ .

 

9) Solution of the equations of the lines in the case of maladjusted line:

Possible the more generic case sees the line sluice to the income on a having generatorV _g inner stiffness Z_g ¹ Z_or and sluice in escape on one stiffness Z_u ¹ Z₀ . The condition on the cargo is therefore , replacing in it the equations of V(s, x) and of I(s, x) is obtained where is the standardized cargo stiffness, such is obtained therefore relationship is called coefficient of reflection on the cargo and concurs to write in compact shape . The condition of closing on the generator is instead that is, defining the stiffness of the standardized generator, from which replacing in which is obtained collecting and defining the reflection coefficient on the 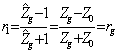generator obtains 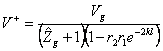that replaced with to in the it gives back .

Ordinary lines in transitory regimen

10) Line LC:

It is a line for which it is supposed are null the longitudinal losses cross-sectional (r) and (g) with this simplification obtains therefore in the case of adapted line has antitransforming has therefore looks at that the v(t, x) in one point x of the line he is equal to the v_g , but only after a time said time of transit, the phase speed is obtained differentiating and uguagliando to 0 the argument of v_g cioè the ž .

 

11) not distorting Line and condition of Heaviside:

Collecting L and C in the propagation constant 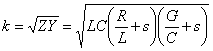is had in which pu² to carry s outside root facilitating the antitransformation on condition that obtaining and therefore in the case of adapted line has whose antitransformed è from which it looks at that it marks them is is delayed that attenuated.

 

12) Pupinizzazione and its problems:

In practical the G conductance it is much lowland, then has therefore in order to approach itself the condition of Heaviside is rerun to the pupinizzazione that consists in inserting of the inductances concentrated along the line in order to increase the inductance distributed of the same one, the problem is that cos¬ making a lot reduced is created of the filters pass-low therefore the line has one passing band.

 

13) Line RC:

A line RC is a line for which G and L are supposed negligible, it is obtained . The antitransformed one that it achieves some is in a generalized manner difficult, except in the case in which in income to the line an impulse is had, in such case in fact obtains a bell that it is as well as more width how many the more us goes away from the long source the line, that prevents to transmit marks them impulsive to frequency elevated on this type of line.

 

14) Approximation of one generic line:

One whichever line can be thought like one series of one line LC and one line RC.

 

15) Stiffness standardized on the generator and the cargo:

 

16) Coefficient of reflection on the generator and the cargo:

 

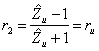
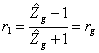
17) Behavior of one line adapted on the generator and maladjusted on the cargo:

The general relation found for the maladjusted lines is applied observing that and that in agreement to the fact that if the generator is adapted not has reflection on it. After all is obtained and considering the center of a line LC for which is had the time of transit of line LC can write being t and analogous therefore obtains therefore will be had that to time t/2 it arrives in the point centers them of the line marks distributed them from the generator to the time t=0 while to time 1,5t arrives in the point centers them of the line marks them that reflection has endured one on the cargo.

 

18) Behavior of one line maladjusted on the generator and maladjusted on the cargo:

The general relation found for the maladjusted lines is applied observing that it is necessary to calculate all the largenesses and that termine the can be developed in series of Taylor.

With analogous considerations to the previous ones the value of v(t is obtained, x) in the point centers them of the line that turns out to be sum of the continuous reflections that are are on the cargo that on the generator. We have seen 3 cases:

to)       line sluice on the cargo on a double stiffness of Z₀ , sluice in having income on a impulsive generator equal stiffness to the half of Z₀ , obtains one series of impulses.

b)       line sluice on the cargo on a double stiffness of Z₀ , sluice in income on a generator to having step equal stiffness to the half of Z₀, obtains a series of steps of more and more small amplitude and that it converges to an ended value.

c)       line opened on the cargo, sluice in income on a generator to step lacking in inner resistance, obtains one series of impulses.

d)       line opened on the cargo, sluice in income on a impulsive generator lacking in inner resistance, is had that in answer to a step a shape of periodic wave is obtained.

Lines in permanent regimen

19) Constant of propagation in permanent regimen:

K =to(w) jb(w)

With to = constant of attenuation of the line e constant b = of phase.

 

20) characteristic Stiffness in permanent regimen:

Z = R₀(w) jX₀(w)

 

21) Equation of the lines in permanent regimen:

The fasori in the equations can be replaced that we had found in the dominion of Laplace

The expression in the time of v(t, x) obtains remembering that it is equivalent to the real part of the rotary fasore that is

famous therefore the presence of a progressive wave and a regressive wave, imposing that the argument of the cosine is constant (…uguagliando to 0 differentiates them) finds the speed of phase for the progressive wave and for the regressive wave.

 

22) Value of the coefficient of reflection to abscissa x of the linea:

 

23) Paper of Smith:

It concurs to determine the stiffness standardized in one point x of the line, in fact through the the coefficient of reflection in x can be calculated being 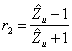with and therefore it is had 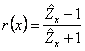. This last one is a relation between complex numbers that a point of the complex plan of the reflection coefficients associates to the complex plan of the standardized stiffnesses.

 

24) Meant of the circumferences of the paper of Smith:

The circumferences that have the center on positive the imaginary axis are those that they have .

The circumferences that have the center on the imaginary axis negative are those that they have .

The circumferences that have the center on the real axis are those that they have , between these the maximum circumference are that one that previews resistance 0, to the inside are the positive values of the resistance you, to the outside us would have to be the values denied to you but that does not have sense in how much the line is passive.

 

25) salienti Points of the paper of Smith:

(-2,0) ž it corresponds to that is to a short circuit, the reflection coefficient is r = -1.

(-1,0) ž it corresponds to that is to the adaptation, the reflection coefficient is r = 0.

(0,0) ž it corresponds to that is to a opened circuit, the reflection coefficient is r = 1.

26) Course of the coefficient of reflection in function of the distance from the cargo for one line LC and one line RC:

Line LC: for a line LC ha k = to jb = jb = therefore the reflection coefficient is where the 1° exponential he is constant therefore is had that r(x) it is a carrier of constant module that wheel in counter-clockwise sense if us crescent is moved towards the cargo…(x) while wheel in counter-clockwise sense if it is moved to us towards the generator; periodic function with period is moreover one .

Line RC: for a line RC ha k = to therefore the reflection coefficient is therefore going towards the generator wheel in hour sense and diminishes the module second a spiraleggiante course in agreement with the concept that one autoadatta infinitely long line.

 

27) Standing wave ratio r :

The tension along the line is that can also be written in function of the reflection coefficient on cargo r₂ in fact raccogliando is had . Observing that the reflection coefficients are all comprised between 0 and 1, the origin for they can be taken in the center of the paper of Smith where the adaptation is had and therefore the reflection coefficient must be worth 0. In such a way graphical expression of can therefore be had one and in such a way be determined of the value maximum and the minimal value defining the important parametro .

In particular it is had that if the line is adapted ROS=1 while if is maladjusted ROS =¥ and this like consequence of the fact that the coefficient of reflection on the cargo can assume only values comprised between 0 and 1 being the relationship between the wave incident and the reflected wave.

 

28) Matrix of the stiffnesses for the line log:

The line log is a pezzetto of line which it is assimilable to symmetrical and mutual a net 2 doors, therefore of its matrix of the stiffnesses he is sufficient to calculate 2 terms on 4. Remembering notes equations

We calculate ₁₁Z and ₂₁Z placing₂ = 0 that is leaving opened the log of line and putting its income a generator of value current impresso_{the 1} and applying the relations of the lines. Taking advantage of the conditions of closing on the generator and the cargo coefficients V andV ^- of the equations of the lines are gained i. is had from which while is obtained from which it is obtained . 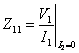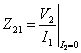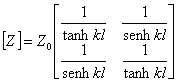In order to calculate e they are necessary V₁ and V₂ , have while Replacing the values it finds obtains Z to you₁₁ and Z₂₁ and therefore can be written the following matrix of the stiffnesses from which in order passing to the matrix of the admittances they must be changed the signs to the terms on the secondary diagonal and be divided for the determining one that it is worth in this case .