External characterization of the circuits

1) As to estimate the time employed from it marks them in order to cross a circuit and relation with the phase and group delay:

Carrying out a amplitude modulation it is succeeded to mark marks them and therefore to estimate the time that it employs to cross a circuit 2 doors. In particular it is necessary to send in income marks them and to consider that the generic function of net of a net 2 doors is n° a complex therefore and therefore being antitransformed has a translation in the time and taking advantage of the developments in series of Taylor it arrests you to 1° the order for e and being Dw®0 is obtained in which 2° the cosine has a slower argument of the first one therefore characterizes the envelope, the delay of group è while the first cosine characterizes the delay of phase .

 

2) regarding Considerations the resonant circuit parallel and the coefficient of Q resonance:

Feeding circuit RLC parallel with a current generator_{the g} and estimating as exited_{the r} it is had:

ž

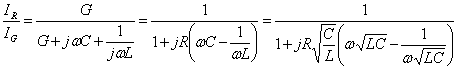
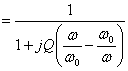having place e .

The effect of the resonance is very visible if the module of the relationship 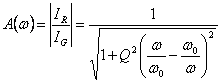is considered which it stretches to 1 for w = w₀ and whose shape of wave is a Gaussian one the whose maximum amplitude is always 1.

For a circuit RLC parallel ha from which one looks at that Q increases if the resistance is high, but this can only happen if L and C are of optimal invoice, such that is not to introduce parasitic resistances which located in parallel to R are in a position to lowering of the value and with it il Q.

 

3) Bandwidth:

It is the interval of frequencies for which the largeness is inferior in order not more than regarding the maximum value that comes assumed in correspondence to the resonance.

 

4) Relation between the Q of a resonant circuit and the bandwidth:

The relation 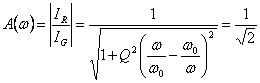is only verified if > > >

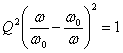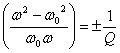allora .

 

5) Door:

Draft of a brace of such clips that the current entering in one is equal in module to the outgoing current from the other.

 

6) Theorem of substitution:

In a net whichever one its portion, accessible from a door can be replaced with an independent generator of tension or current, having like largeness impressa the correspondent largeness door electrical worker. If the remaining net is introduced like a generator, the bipole that must be connected is an independent generator of the opposite type.

 

7) Theorem of Thevenin:

An accessible net from a door is equivalent externally to the door, to the same net in which the excitations they have been disattivate with in series to the door a generator of having tension equal tension impressa to the tension that manifest to empty in correspondence to the door of the net and with the same polarity.

It is demonstrated replacing the right net with a current generator and applying the theorem of superimposition of the effects in order to calculate V_{the AB} to the door. When the generator of current V _AB =V is opened₀ , when disattiva net V_AB= disattivata I(rete).

 

8) Like applying Thevenin if the inner outline to the net is not famous:

to)       measure V_{the AB} letting the open net.

b)       the net on a variable resistance is closed of which the value until to having to its heads is changed , is to such caught up point the adaptation and the stiffness of the net is equal to the stiffness of the cargo.

 

9) Theorem of Norton:

An accessible net from a door is equivalent externally to the door, to the same net in which the excitations circuit of the door has been disattivate with in parallel to the door a generator of having current equal current impressa to the current short.

It is demonstrated like Thevenin but applying a tension generator.

 

10) Theorem of the maximum transfer of active power:

A bipole fedZ _u from a generator of tension of inner stiffness Z_g absorbs from this the maximum active power when its stiffness is worth Z_g^* .

is had

The term lowers the power therefore us servants who are null that is obtain therefore 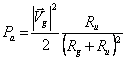that the power assumes its maximum forR _u =R _g therefore after all is maximum if .

In such case it is had but distortion del marks them, therefore for having the maximum active power maintaining it marks not distorted them, the cargo stiffness and the stiffness del circuit must be equal and both real ones.

 

11) Wave incident and wave reflected on a bipole, coefficient of reflection:

It is possible to write 2 relative largenesses to a bipole as linear combination of v and i cioè with opportune chosen of the coefficients ha 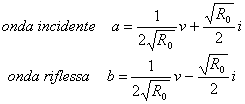from which inverting ed is had where R₀ is one constant of normalization.

The reflection coefficient is .

 

12) Tie between the coefficient of reflection r and the maximum transfer of active power:

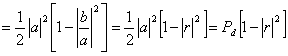looks at therefore that the active power is maximum and coincides with the power available when the coefficient of 0 reflection is that is Z_u = R₀ .

 

13) Net 2 doors:

Draft of an accessible circuit from 2 doors and lacking in excitations to its inside.

 

14) Like obtaining the coefficients of the matrix stiffnesses to empty [ Z ]:

This matrix satisfies the relation 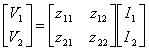therefore in it variable the independent ones is the currents, it can be applied to the principle of the superimposition of the effects constructing 2 equivalent circuits that concur everyone to calculate 2 largenesses of the matrix, in particular placing a generator of current_{the 1} to the income of the net 2 doors and leaving opened the escape door therefore₂= 0 can be found i ₂ values ofV ₁ andV and therefore ₁₁Z and Z₂₂ , while placing a current generator₂ to the escape and leaving opened the income are estimated the others 2 largenesses of the circuit.

 

15) Like obtaining the coefficients of the matrix admittances to empty [ Y ]:

This matrix satisfies the relation 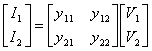therefore in it variable the independent ones is the tensions, it can be applied to the principle of the superimposition of the effects constructing 2 equivalent circuits that concur everyone to calculate 2 largenesses of the matrix, in particular placing a generator of tension V₁ to the income of the net 2 doors and cortocircuitando the door of escape therefore V₂= 0 can be found the values of_{the 1} and_{the 2} and therefore ₁₁Y and Y₂₂ , while placing a generator of tension V₂ to the escape and cortocircuitando the income the others are estimated 2 largenesses of the circuit.

 

16) Like obtaining the coefficients of empty the hybrid matrix to [ H ]:

This matrix satisfies the relation 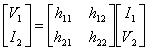therefore in it variable the independent ones is the income current and the escape tension, can be applied to the principle of the superimposition of the effects constructing 2 equivalent circuits that concur everyone to calculate 2 largenesses of the matrix, in particular placing a generator of current_{the 1} to the income of the net 2 doors and cortocircuitando the door of escape therefore V₂= 0 can be found i values of V₁ and I₂ and therefore h₁₁ and h₂₂ , while placing a generator of tension V₂ to the escape and opening the income the others are estimated 2 largenesses of the circuit.

 

17) Like obtaining the coefficients of empty the inverse hybrid matrix to [ G ]:

This matrix satisfies the relation therefore in it variable the independent ones is the escape current and the income tension, can be applied to the principle of the superimposition of the effects constructing 2 equivalent circuits that concur everyone to calculate 2 largenesses of the matrix, in particular placing a generator of tension V₁ to the income of the net 2 doors and opening the escape door therefore₂= 0 can be found the values of I₁ and V₂ and therefore g₁₁ and g₂₂ , while placing a generator of current_{The 2} to the escape and cortocircuitando the income are estimated the others 2 largenesses of the circuit.

 

18) Like obtaining the coefficients of the matrix of transmission [ T ]:

This matrix satisfies the relation 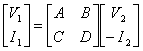therefore in it variable the independent ones is on the same door that it renders necessary I use it of the nullore in order to calculate of the coefficients, in particular pu² to apply to the principle of the superimposition of the effects constructing 2 equivalent circuits that concur everyone to calculate 2 largenesses of the matrix, in fact placing a generator of tension V₂ to the escape of the net 2 doors and in series to it a nullatore, is had that₂ = 0 and the values of I can therefore be found₁ and V₁ and they to calculate To and C, while placing a generator of current_{the 2} to the escape and in parallel to it a nullatore, is had that V₂ = 0 and the values of I can therefore be found₁ and V₁ and they to calculate B and D. In both the cases on the income door a noratore is had so that tension and current on the same one can vary liberations.

 

19) Condition for respecting for the logon of nets 2 doors:

When 2 doors join of the nets, the condition must always be respected for which in the nets 2 constituent doors, the current entering in the clip of a door must be always equal to the outgoing current from the other clip of the same door.

20) Stiffness of the series of 2 nets 2 doors:

It is worth the customary relation of the series, is demonstrated observing that the current entering in 1ª the door of the net To is equal to the current entering in 1ª the door of the B net while the tension applied in income to the two nets is the sum of applied the singularly tensions, is had:

 

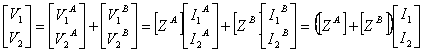
21) Tests of validity in the logon case series-series:

Based on the substitution theorem a current generator can be put is in income that in escape the net and to consider separately the effect of the two generators being applied the superimposition of the effects

It must be verified that the current that slides in the common branch to the 2 escapes is null when the circuit of escape of the total net is opened and therefore current does not slide in it while in income a current generator is applied. Analogous it must be verified that the current that slides in the common branch to the 2 incomes is null when the circuit of income of the total net is opened and therefore current does not slide you, while in escape a current generator is applied. The test always is verified if a transformer in escape from one of the 2 doors is placed because in such a way they impose to behave themselves correctly to the door that is sluice on the head physician, the other door of the same net must make equally and therefore making the same one also for 1ª the door of the B net and for the second one is had consequently.

 

22) Admittance of the parallel of 2 nets 2 doors:

It is worth the customary relation of the parallels, is gained observing that the tensions applied in income to the single door are equal while the current is the sum of the currents, are had:

 

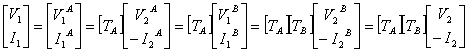
23) Tests of validity in the logon case parallel â " parallel:

It must be verified that the current is null that slides between the escapes of the nets 2 doors members when cortocircuitano the escapes of the total net and a generator of tension in income to it is placed. Analogous it must be verified that the current is null that slides between the incomes of the nets 2 doors members when cortocircuitano the incomes of the total net and a generator of tension in escape to it is placed. The test always is verified if an ideal transformer is placed in cascade to one of the 2 nets with unitary relationship of transformation.

 

24) Matrix of transmission of one falled of 2 nets 2-doors:

It is demonstrated proceeding from the income towards the escape using the T matrix for every net 2 doors, is had:

 

25) equivalent Circuit:

One obtains from the relations that it gives to place to the corresponding matrix (stiffnesses, admittances …) associating to the mixed terms of the generators controls to you, and to the homogenous terms of the stiffnesses or the trasmittenze.

 

26) mutual Net 2-doors:

It is a net for which if we consider 2 various situations (1) and (2), the largenesses electrical workers to the doors respect the following equality:

Being the tension to the door of income in the situation the 1 and current to the door of escape in situation 2.

 

27) symmetrical Net 2-doors:

It is a net for which the door of income and the door of escape can be exchanged vicendevolmente without to provoke external consequences to the same net.

 

28) Relation between symmetry and reciprocity:

The symmetry implies the reciprocity but it is not true that a mutual net must necessarily be symmetrical.

 

29) Demonstrate that every bipole is mutual:

It must be demonstrated that dates 2 situations various electrical workers, are respected the relation of Lorentz but is had and also then obtains that equality is sure one.

 

30) Relation between one net 2 doors constituted from bipoles and the reciprocity:

A net 2 doors constituted from connected bipoles however is mutual. It is demonstrated closing the net 2 doors on 2 generators of current, this can be made in virtue of the substitution theorem, is clearly therefore that the door largenesses will coincide with the largenesses impresse. Applying Tallegen they are valid the 2 relazioni

But the two summary ones are equal because every singularly taken bipole is mutual therefore obtains that it is just the condition of reciprocity of Lorentz.

 

31) Consequences of the reciprocity on the representation of the nets 2 doors:

For [ the Z ] Z ₁₂= Z ₂₁is had while for [ the T ] determining unitarian has itself, such conditions can be determined to leave from the various operating situations that concur the calculation of the parameters of one given matrix, and replacing them in the condition of Lorentz.

 

32) Consequences of the symmetry on the representation of the nets 2 doors:

For [ the Z ] the elements on the diagonals are equal between of they while for [ the T ] determining unitarian has itself and To = D.

 

33) Matrix of the stiffnesses for one net to âTâ?:

where Z_C is the stiffness mails in parallel.

34) Matrix of the admittances for one net to â?pâ?:

where Y₁ and Y₂ are the stiffnesses placed in parallel.

 

35) Matrix of the admittances for one net 2-doors to âT derivatoâ?:

The net can be seen like parallel of 2 nets, one to âTâ? and constituting from a single resistance that connects the income with the escape, the matrix turning out admittance is the sum of the matrices admittance of these 2 nets.

 

36) Matrix of the admittances for one net 2-doors to âdoppio Tâ?:

The net can be seen like parallel of 2 nets to âTâ?, therefore the matrix turning out admittance is the sum of the matrices admittances of these 2 nets.

 

37) Parameters image:

Draft of 4 parameters (2 stiffnesses images Z_i1 and Z_i2 and 2 exponents of trasduzione on base image g₁₂ and g₂₁) which under opportune conditions concurs to estimate the behavior of one simply net constituted from one falled more nets.

38) Stiffnesses images:

The stiffness that looks at in income to a net 2-doors sluice on a Z stiffness_u is function is of Z_u that of the net 2 doors, in particular using the equations of the matrix [ Z ] and the condition of closing and is found and analogous if the income is closed on Z_U , the stiffness seen from the escape door è . the stiffness Z image_i1 is such that when we close door 2 on Z_i2 it has Z_i1 = z_i1 and when we close door 1 on Z_i1 has Z_i2 = z_i2 .

39) Closing on base image:

One cascade of nets 2 doors says sluice on base image when every component net sees to its left own stiffness Z image_i1 and to the own right the analogous Z_i2 .

 

40) Exponent of trasduzione on base image income-escape:

It describes the transfer of marks them, it is supposed that the net 2 doors is excited in way whichever to the income door and sluice on the stiffness Z image_i2 , has:

 

41) Exponent of trasduzione on base image escape-income:

It describes the transfer of marks them, it is supposed that the net 2 doors is excited in way whichever to the escape door and sluice on the stiffness Z image_i1 , has:

 

42) Property of one falled of nets 2 doors on base image:

to)       the stiffnesses Z image_i1 of ognuna they coincide with the stiffness image of the first door and the stiffnesses Z image_i2 coincide with the stiffness image of the last door.

b)       the trasduzione exponents are equal to the sum of respect exponents to you of trasduzione of the single constituent nets.