Systems of enslavement

1) System of enslavement :

Draft of a system in which the income is variable in the time with one dynamics comparabile with that one of the same process and therefore is important beyond to the detailed lists to regimen also the detailed lists on the transitory one.

 

2) basic Detailed list of a whichever system :

Whichever system must always be characterized from the stability.

 

3) relative Detailed lists of planning to the behavior to regimen :

to)       type of system that is number of poles in the origin.

b)       error to regimen in correspondence to a data canonical income of reference.

 

4) Detailed lists in the dominion of the time :

They are reported to the indiciale answer, of customary closed cycle, they are:

Time to the eminvalore :

time interval that the indiciale answer employs in order to reach half of the regimen value.

Time of answer:

time interval that elapses between the 0.1 and the 0,9 of the value of regimen of the indiciale answer.

Sovraelongazione :

the caught up maximum value from the indiciale in case sovraelongante answer.

Pseudoperiod :

It is the period of the oscillations dampened present in the indiciale answer, is estimated to leave from 2ª the intersection of the indiciale answer with the regimen value.

Time of arrangement :

It is the time in correspondence of which the indiciale answer catches up the 0,05 of the regimen value.

 

5) Detailed lists in the dominion of the frequency :

With reference to the harmonic answer, it is had:

Module to the resonance :

the assumed maximum value from the module of the harmonic answer.

Pulsation of passing band :

pulsation for which the module of the harmonic answer is reduced of 3dB regarding the value that assumes for w®0.

with reference to the harmonic answer to open cycle they are considered instead the margin of gain m_g, the margin of phase m_j and the pulsation of attraversamento w_t .

 

Syntheses for tried to you in the dominion of jw

6) Typology of systems for which the synthesis for tried to you is used in jw :

It comes used for having systems to minimal phase that is all the poles and the zeroes in the left semiplan

 

7) total Ties:

Draft of formulas empiricists who tie the detailed lists in the time with the detailed lists in frequency, the more important are:

on condition that the sovraelongazione S is smaller of 0,1

on condition that the module to resonance M_r is comprised between 2dB and 4dB.

8) Considerations on the detailed lists in the synthesis in jw :

The detailed lists that are given in the dominion of the time t_r and S must be tramutate in detailed lists in the dominion of the frequency w_B and M_r through relazioni the e moreover he is easyr to plan the compensator to open cycle therefore is necessary to pass from the detailed lists closed cycle w_B and M_r to the detailed lists to open cycle m_j and w_t .

 

9) Utilizzo of the paper of Nichols in the passage from the detailed lists to the detailed lists to open cycle:

It comes used the paper of Nichols in how much the same relative curve to the harmonic answer, if read in cartesian coordinates expresses the same one to open cycle while if read in curvilinear coordinates along the curves to constant module, expresses the harmonic answer. Memories that the intersection of the F(jw) with the axis to 0dB characterizes the phase margin and the corresponding pulsation is said attraversamento pulsation w_t .

 

10) Passage from the specific one on the module to the resonance to the margin to the specific one on the phase margin:

M_r on the paper of Nichols he is equal to the value of the curve to elevated constant module more that he turns out tangent to the G(jw), the intersection of such curve to constant module with the axis to 0dB characterizes a phase margin that is senz' other minor of the margin of phase of the G(jw) therefore, assuming it like specific, has also a safety margin. In truth the module to resonance M_r is comprised between 1dB and 5dB to which margins of phase m correspond_j comprised between 54° and 33°.

11) Passage from the specific one on the band passing w_b to the specific one on the attraversamento pulsation w_t :

the pulsation of attraversamento w_t on the paper of Nichols is characterized from the intersection between the G(jw) and the straight one to 0dB, the passing band w_b instead is characterized from the intersection between the G(jw) and the curve to constant module to -3dB, this intersects the axis to 0dB for j= - 90°. Considering that the pulsations grow from high towards the long bottom the curve that represents the G(jw) and observing that the margin of phase for a stable system is 30° < m_j < 60° < < 90°, it is had that the specific one on w_b is respected if w_t < w_B , ulterior considerations carry to assert that it must be:

12) Nets standard :

All having are three typology standard unitary gain and of which third it is constructed coupling the first two:

to)       ritardatrice or attenuatrice net

b)       anticipatrice net

c)       net to saddleback

 

13) ritardatrice Net :

A pole in the left semiplan is obtained posizionando and a zero to its left, come used laddove are wanted to be reduced the attraversamento pulsation in case not there are problems R-with regard to the phase, from the diagrams of Bode evince in fact that such net concurs is to attenuate that to insert a delay. In truth the ritardatrice net is not a lot used just because attenuating the attraversamento pulsation diminishes w_t , with it diminishes the passing band w_B and therefore the time of answer t_r of the system infatti ones has and the general expression of such net is 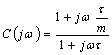with m that varies between 2 and 16 and concurs to move the position of the zero regarding the pole.

 

14) anticipatrice Net :

A zero in the left semiplan are obtained posizionando and a pole to its left, comes used laddove for one given w_t is wanted to be increased the phase margin, from the diagrams of Bode this net but beyond anticipating is observed that increases also the gain and therefore w_t, being the diagram of such effect is made decreasing monotone comes compensated increasing of a 10% the phase richiesta.L' general expression is 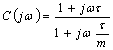with m that varies between 2 and 16 and concurs to move the position of the pole regarding the zero.

 

15) Syntheses for tried to you in the dominion of jw :

Syntheses for tried to you are necessary to iterare the following procedure be a matter itself of one:

to)       the precompensated system is satisfied specific on the error to regimen obtaining

b)       the specific one is satisfied on the passing band making that the corresponding pulsation w^* is greater of the w_t of the precompensated system, such aim can be operated in the two following ways:

1)       a ritardatrice net becomes part that therefore reduces the w_t but the phase diminishes also, if that inficia the specific one on the margin of phase m_j is necessary to introduce one totally anticipatrice net therefore necessity of one complex net to saddleback

2)       in case origin in way is possible is convenient to insert a pole nell' to svincolare specific sull' the error to regimen dal gain and then to reduce this last and with it w_t .

c)       satisfies the specific one on the module to the resonance that goes translate in a specific one on the margin of phase through the appropriate table and, in case necessary, becomes part therefore a anticipatrice net which but increases also the module for which attention must be made that it does not become w_t > w^* . In order to plan the anticipatrice net it can be operated in one of the two following ways:

1)       in correspondence of w_t how much is looked at must be the variation of the phase in order to satisfy the specific one on the margin of phase m_j and to the found value a 10% must be added intrinsic in the use of the anticipatrice net

2)       posiziona on the wished pulsation w^* and currency it is the increment of phase in order to satisfy the specific one on the phase margin, than the eventale increment of the module necessary in order to move w_t in w^*.

 

Syntheses for tried to you in the dominion of the variable one s

16) When the synthesis for tried to you is used in s :

In the case of simple systems to not minimal phase or when they come supplied of the detailed lists in the dominion of the time which damping x , the natural pulsation w_n and the constant principle of permissible time t for the system.

17) Effect of the limitation of damping x on the place of the roots:

It is had that the place must be comprised in the left semiplan between straight passing for the origin and forming with imaginary the 2 axis an angle whose arcoseno is equal to damping x .

18) Effect of the limitation of the natural pulsation w_n on the place of the roots:

The place of the roots must be comprised in the left semiplan to the inside of 2 straight horizontals whose ordered it corresponds to the resonance pulsation that for a data damping x is tied to the natural pulsation w_n from the relation .

 

19) Effect of the limitation of the constant principle of time on the place of the roots:

The place of the roots must be comprised to the left of straight vertical passing for the smallest pole correspondent to the maximum time of climb that the system can introduce.

 

20) Considerations on the zeroes to positive real part:

They are not a physical truth, they are generated when in order to hold account of the delays the exponential with the developments in series of Mac Laurin is approximated.

 

21) As to stabilize the systems to not minimal phase:

It is necessary to add a number of zeroes in the such left semiplan that the excess poles-zeroes is equal to but to the contempo, affinchè the compensator he is physically realizable, it must be added a not smaller number of poles of the number of zeroes , in order to satisfy both the detailed lists the poles that must necessarily be introduced come places to the infinite where they do not have infuence while the zeroes come places much neighbor to the origin so as to to attract the barycentre. In short must be made that for a data gain interval all the coppers of the place are contained to the inside of the region delimited from the detailed lists on x ,w_n and t .

 

Direct synthesis

22) Philosophy of the direct synthesis:

It is proposed to us of having a function of transfer W(s) of type standard independently from the process, to such aim the compensator is planned so as to to carry out of the cancellations in the function of transfer to open cycle P(s) of the process to compensate, ci² it determines that this synthesis is applicable to systems to minimal phase in how much the cancellations in the left semiplan is only possible only for the ideal systems.

 

23) Typology of direct synthesis:

In the synthesis to a freedom degree the U(s) income is had only while in the synthesis to two degrees of freedom it is had is the U(s) income that the D(s) disturbance.

 

24) Relation that describes the compensator:

The function of transfer closed cycle must be famous wished , inverting this last one obtains the expression of the compensator .

 

25)Function of transfer closed cycle and value of the coefficients:

where the produttoria to denominator indicates of the far poles that come inserted in order to guarantee the physical realizability of the compensator while the coefficients of the trinomio come chosen on the base of the answer to the transitory demand, therefore:

to₁ = 2xw_n

to₀ = w_n²

while the terms to numerator come chosen on the base of the value of the error to regimen, in particular:

to) in the case that demands an error to null regimen for incomes of type step:

b₀ = to₀

b₁ = whichever

b) in the case that demands an error to null regimen for incomes of type rampa:

b₀ = to₀

b₁ = to₁

the value of such coefficients is determined from considerations on the function of transfer of error in the case of unitary feedback .

 

Synthesis for allocation of the poles

26) Philosophy of the synthesis for allocation of the poles:

He is applicable to every system, it is to minimal phase that not, is based on imposing the position of the zeroes of the function of transfer closed cycle and consequently the coefficients of the compensator are determined whose denominator must possess degree l ³ n-1 being n the degree of the denominator of the process to compensate, while the numerator of the compensator possesses the same degree of the denominator of the same one.

Synthesis for allocation of the autovalori

27) Synthesis for reaction from the state:

A linear system is had and stationary controlable del which are state notes all variable that is the carrier of state, a carrier of gain K _c is wanted to be determined which it concurs to make that the autovalori della dynamics matrix correspondent al arranges is all in one determined region del slowly complex in agreement with the result that is desired to obtain dal arranges, to example if the asymptotic stability is demanded these autovalori must find all nel semislowly left. If the matrix To is in controller shape it obtains that the last line of To_c less has the equal coefficients of the sign to the coefficients of the polynomial characteristic and therefore a system of equations of 1° the order is obtained from which gaining K_c that gives back the polynomial characteristic desisderato.

The problem of this synthesis is that it is necessary to know all the carrier of state that can be complex and expensive.

 

28) Formula of Ackermann for the feedback from the state:

It concurs to characterize the carrier K_c when the matrix To_c is not mail in similar shape, avoiding in such a way the tortuoso passage to the same one, has:

being the image of To through polynomial characteristic P_c(To).

 

29) Esteem of the state :

In the synthesis for reaction from the state it was necessary to know all the carrier of state while the state esteem is a tipologia of synthesis that gains the value of the state of the system on condition that it is observable and is notes the largenesses of income and escape of the same one.

 

30) estimated State :

Draft of the carrier that is obtained in escape from the having system as incomes the largenesses of income and escape of the assigned system, and that it satisfies the relation .

 

31) Observer of the state :

S' means the dynamic system that carries out the esteem of the state, also is said appraiser and is described from the state equation , scope of the esteem of the state is to characterize the F matrices, h, g so that the state satisfies the to such aim is transformed according to Laplace is the equation of the system that the equation of the observer and equals the transfer functions, is obtained .

Collecting to 1° the member the coefficients of and extracting the term this last one pu² to simplify itself and obtains from which it is deduced that for the appraiser is had and .

In order to gain the carrier g dynamics of the esteem error must be gained, in particular has therefore finds that the error of the esteem has the same dynamics of the esteem that it implies that we choose g so as to to have an asymptotically stable appraiser, the esteem error stretches independently to 0 from the error begins them therefore must be chosen g so that the autovalori of the matrix are all to negative real part. If the matrix To₀ is in observer shape it obtains that the last column less has the equal coefficients of the sign to the coefficients of the polynomial characteristic and therefore a system of equations of 1° the order is obtained from which gaining the carrier g that it gives back the polynomial characteristic.

 

32) Considerations on the choice of the autovalori of the matrix To₀ :

They are senz' other to negative real part, moreover on they dynamics of the appraiser depends which must be faster than at least a order of magnitude regarding dynamics of the system and therefore these autovalori must be found more much on the left regarding the autovalori of the system.

 

33) Formula of Ackermann for the esteem of the state:

It is a formula that concurs to calculate the carrier g when the matrix is not in canonical shape of observer, ha:

where is the image of To through polynomial the characteristic P_or(l).

 

34) Property of separation:

It is an important property that one refers to the synthesis for feedback from the estimated state, concurs to plan separately and independently the carrier line k_c and the carrier column g, ha .

It is obtained placing the observer in the outline to feedback, write therefore the equations of the system

from which replacing the in the 2ª and replacing this in before and considering as carrier of state for the retroazionato system the equations are obtained which the matrix dinamica corresponds and remembering that the polynomial characteristic for a triangular matrix it is obtained like product of the terms on the diagonal, the theorem is demonstrated.