Property of the systems in the state space
1) Norm of one matrix:
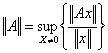
being defined in terms of the norm of x obvious that various it is chosen for ||x|| they involve different norms of To.
2) Equilibrium of a system of equations differentiates them:
Assuming that the system 
admits the
banal solution x = 0 this it comes assumed as equilibrium and is
assumed that the relative solution al point begins them x0 exists around in one its.
3) stable Equilibrium :
The equilibrium is said to be stable if for every and > 0 a d exists > 0 such that 
every for t³t0 and on condition that ||x0|| < d . In
short it is had that if the point begins them x0 it is contained in one ipersphere of centered beam d in t0 then is had that the solution of the system of
equations differentiates them remains confined in a ipercilindro of
beam and around the axis t that
involves that if the equilibrium is stable in correspondence to time
t=t0 then is stable in
correspondence to whichever 0 time beginsthem t 1>t
also to choose an opportune value for d.
4) attractive Equilibrium :
The equilibrium turns out attractive being if it exists h> 0 such that ha 
for every ||x0|| < h .
5) asymptotically stable Equilibrium:
The equilibrium is said asymptotically stable if it is at the same time is stable that attractive.
6) asymptotically total stable Equilibrium:
Draft of the case in which as value begins them it takes a various point from the origin.
7) unstable Equilibrium :
The equilibrium of the equation differentiates them is unstable if he is not
stable.
8) Conditions of equilibrium for a linear and stationary system :
The solution of the equation of state in the stationary
case is 
considering initially absence of
forcing quindi 
is observed that the solution is
linear combination of 
terms where l is the autovalore of the
dynamics matrix and r its variety, is had therefore that the
equilibrium is asymptotically stable if all the roots of the polynomial
characteristic of the matrix To have negative real part, if also a
single one of they is to positive real part, the equilibrium is
unstable.
In the case instead that varieties 1 are having roots to null real part then, relatively to they, the system is stable but not asymptotically stable while the system is unstable if the roots to null real part have greater variety of one.
Considering also the forced answer, it is had that the
system turns out stable if the autovalori of the dynamics matrix are
all to negative real part and the forcing is limited in fact 
.
9) controlable State :
One state is said to be controlable in correspondence to a
time t>0 if a function of such permissible income exists u that
is had the space of the controlable
states is indicated with Xc.
10) Matrix of controllability :
it concurs to exactly characterize to the inside of the space of state the sottospazio of the controlable states determined from the image of this matrix.
11) fundamental Characteristic of with of the controlable states :
With of the controlable states it does not depend on the time t, this only in theoretical way in how much for a real physical system, to pass from one be not null to one be null in an arbitrary time could demand a so wide income to send in saturation some element of the system.
12) controlable System :
It is a system for which with of the controlable states it coincides with the state space, that happens if the controllability matrix has the maximum rank, that is is invertible.
13) raggiungibile System :
A system is said to be raggiungibile if assuming that the state begins them is null x(0) = 0, can be made in way to catch up a determined final state xf al time t being applied an opportune income between 0 and t.
14) Shape of Kalman for the controllability :
If the rank of the controllability matrix is not maximum, and therefore the space of the controlable states is smaller of the state space, it is necessary to choose as base for the state space a base whose first the remaining carriers are a base for the space of the controlable states and carriers is whichever purchè in opportune number.
In the new base the system is described from the matrices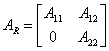 
; 
; 
, moreover the state carrier
can be partizionato in relative 
a carrier to the
controlable states and vettore 
a relative to
the not controlable states, the state equations can easily be
estrinsecare and they to deduce the equivalent outline to blocks.
The transfer function that gains 
is
relative to the described controlable subsystem only givesto 11 , b1 , c1 .
15) Shape of Jordan for the controllability :
If the dynamics matrix To is diagonalizzabile, then the system is controlable on condition that the members of the carrier of income transformed in the new base are all not null. If instead he is not diagonalizzabile, then it is necessary to transform it in the canonical shape of Jordan and the controllability condition is that the members of the carrier of transformed income b the correspondents to the last lines of the blocks of Jordan that constitute the transformed matrix are not null.
16) indistinguishable State from state 0:
One state x is indistinguishable from state 0 in the
interval (0,t) if it is worth the relation 
con 
, that is if to the state corresponds
one answer in null free evolution in the interval (0,t).
17) not observable States:
One state is not observable if he is indistinguishable from state 0. The space of the not observable states is indicated with Xnot.
18) Matrix of osservabilità :
It is the matrix 
, it concurs to
exactly characterize to the inside of the space of state the
sottospazio of the not observable states determined from the nucleus
of this matrix.
19) observable System :
A system is observable if with of the not observable states it has null dimension therefore do not exist be inosservabili various from zero, that happens if the osservabilità matrix has the maximum rank that is the nucleus (…that it characterizes the not observable states) coincides with with empty.
20) Shape of Kalman for the osservabilità :
If the nucleus of the osservabilità matrix does not have null dimension, is necessary to choose as base for the space of remaining state a base the whose first carriers are a base for the space of the not observable states and carriers is whichever purchè in opportune number. In the new base the system is described from the matrices:
;
;
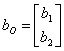moreover the state carrier can be partizionato in
relative 
a carrier to the not observable states
and relative 
a carrier to the observable states,
the state equations can easily be estrinsecare and
they to deduce the equivalent outline to blocks. The transfer
function that gains 
is relative to the
described observable subsystem only givesto
22 , b2 , c2 .
21) Shape of Jordan for the osservabilità :
If the dynamics matrix To is diagonalizzabile, then the system is observable on condition that the members of the carrier of escape transformed in the new base are all not null. If instead he is not diagonalizzabile, then it is necessary to transform it in the canonical shape of Jordan and the osservabilità condition is that the members of the transformed carrier of escape cj correspondents to the first lines of the blocks of Jordan that constitute the transformed matrix are not null.
22) canonical Decomposition of Kalman :
It is necessary to determine 4 bases:
to) B1 is one base for the controlable and not observable states
b) B2 is a completion of B1 to a base for the space of the controlable states
c) B3 is a completion of B1 to a base for the space of the not observable states
d) B4 is a completion of B1 ? B2 ? B3 to one base of "4
in the base of "n that it obtains giustapponendo the carriers of the previous bases, the system is described from the matrices:
;
;
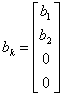moreover the state carrier can be partizionato in:
one carrier x1(t) reported system to the controlable
one carrier x2(t) reported system to the controlable e observable
one carrier x3(t) reported to the not controlable system e not observable
one carrier x4(t) reported to the not controlable system e observable
An important result is that the transfer function
that gains is relative only to the
controlable and observable subsystem.
23) Condition affinchè a system is observable and controlable :
It must be written in minimal shape that is the transfer function must not have cancellations.
24) lawful Cancellations :
A cancellation is said lawful if the associated way to it is stable.
25) Realization :
S' means the passage from the representation by means of the function of transfer to that one in the state space.
26) Realization in canonical shape of controller :
Draft of the passage from the function of transfer to the controllability matrix.
where b0 …bm are i coefficients of the numerator of the function of transfer and to0 …ton-1 are the coefficients of the monico denominator of the same one. The matrix of controllability of this system independently turns out to be of the maximum rank from the fact that us has been or little cancellations and therefore the system is sure controlable.
27) Realization in canonical shape of observer :
Draft of the passage from the function of transfer to the osservabilità matrix
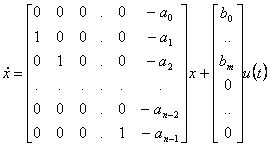
where b0 …bm are i coefficients of the numerator of the function of transfer and to0 …ton-1 are the coefficients of the monico denominator of the same one. The matrix of osservabilità of this system independently turns out to be of the maximum rank from the fact that us has been or little cancellations and therefore the system is sure observable.
28) Realization in canonical shape of Jordan :
Draft of the passage from the function of transfer to the shape of Jordan, it is particularly useful in the case that the denominator of the transfer function is easy fattorizzabile, and therefore the residual ones can be calculated, can be set up the problem in two various ways obtaining only turn out to you equal for that it regards the dynamics matrix To.
As an example considering a triple pole and two simple poles the associate equations of state are:
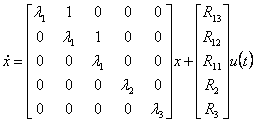
