The place of the roots

1) Place of the roots:

It is one technical that concurs to graphically represent the effects of the passage from opened cycle, in short is had that to varying of the gain k the poles are moved in such a way determining the stability or the instability of the system, moreover from real poles to open cycle they can also be created of the complex poles conjugates to you closed cycle which if the system is stable determines an oscillating answer dampened due to x and w_i that in the detailed lists it comes demanded of light entity.

2) System to regular stability:

It is a system that turns out stable for an interval of the comprised gain k between 0 and a value advanced limit k_Lthat can coincide with ¥ , such gain characterizes the poles mails on the imaginary axis. It is spoken about system to paradoxical stability in how much increasing the và gain towards the stability.

3) System to conditioned stability:

It is a system that is stable if the gain is contained in an interval of the comprised gain k between two ended values.

4) System to paradoxical stability:

It is a system that turns out stbile for an interval of the gain comprised between a value ended limit k_L and ¥.

5) positive Place :

Also place of the roots is said and corresponds to the position of the roots of the characteristic equation of the function of transfer of the closed loop system for a gain k > 0.

6) complementary Place:

Also place is said negative and corresponds to the position of the roots of the characteristic equation of the function of transfer of the closed loop system for a gain k < 0. It is important for the study of the systems to positive feedback, and in the case in which a system it is stable for values only denied you of k.

7) fundamental Relation for the construction of the place of the roots :

Being it is had that the characteristic equation is verified if that condition implies one on the modules and one condition on is made.

8) Condition of the modules :

The fundamental relation is verified as far as the modules if the module of the trasferenza to open cycle is , this condition does not concur to trace the place in how much for every k is satisfied from infinites points of the plan, however once that the place has been traced through the condition on the modules it concurs to graduate it in k in fact for every point s the pertaining to the place can be gained the k to associate it which relationship between the produttoria of the lengths of the carriers that combine the poles of the F(s) with s and the produttoria of the lengths of the carriers that combine the zeroes of the F(s) with sthe that is .

9) Condition of is made :

The fundamental relation is verified as far as makes if the phase of the trasferenza to open cycle F(s) è positive entire being r or a null one. In short a point s of the complex plan belongs to the positive place if the sum of the angles regarding the horizontal plan of the carriers traced from the zeroes and the poles of the F(s) towards the point s is multiple odd number of ±180°. In practical it is used r=0 and for k>0 it is taken less.

10) Branch of the complete place of the roots :

It is the place of the points of the covered complex plan from one of the roots of the characteristic equation when k it varies between -¥ and ¥ .

11) copper Number of the place of the roots :

The copper number is equal to largest between the number of the poles n and number of zeroes m of the function of transfer to open cycle F(s).

12) Points of the place of the roots correspondents to k = 0 :

They are the poles of the F(s) in fact , replacing k=0 is obtained .

13) Points of the place of the roots correspondents to k = ±¥ :

They are the zeroes of the F(s) in fact from the condition on the modules has in fact for k®¥ has 0 to 2° the member and therefore in order to verify the 0 equality NumF(s) must be also that it happens if we find ourselves in the zeroes of the F(s).

14) Simmetrie of the complete place of the roots :

A symmetry regarding the real axis is had always in fact the characteristic equation is to real coefficients therefore its roots is real or to conjugated complex braces. Simmetrie of poles are possible also and zeroes respect to other aces which must necessarily be vertical in how much obtain for geometric transformations dell' real axis that must but always respect the symmetry respect to one brace of poles.

15) copper Number with which the positive place diverges to infinite and relative angle :

The positive place diverges to infinite with |n-m| coppers, the angle is worth , with r entire positive therefore if a system introduces an equal excess poles-zeroes to 0 does not have sense the schematizzazione of the 0 to the infinite. One deduces from the condition on is made observing that when the point goes to the infinite all the carriers that combine it with poles and zeroes are parallels therefore have the same phase. It is observed that the asymptotes therefore characterize do not make part to you of the place and therefore is the coppers of the positive place that those of the place negative can intersect the same asymptotes.

16) Barycentre of the place and formulas in order to characterize it :

Draft of the point of the real axis that turns out to be intersection of the 2|n-m| asymptotes, in the closed loop systems it turns out invariant being to varying of k, is characterized from the formula which pu² to simplify itself considering the sun you leave real since poles and zeroes are complex conjugate to you and therefore the imaginary parts elidono.

17) Conditions of belongings of the positive place to the real axis :

All the points of the real axis belong to the positive place that leave to their right a altogether uneven number of real poles and real zeroes of the function of transfer to opened cycle, count everyone to you with the respective variety. It is demonstrated to leave from a condition on is made observing that the carrier that combines a pole with a point s corresponds a contribution in phase of -180° if the pole is found to right or of 0° if the pole is found on the left of the point s, while if to right of the point s a zero are found, the contribution in phase is of 180°.

18) Angle of departure from a pole:

It is the angle with which the branch of the positive place goes away from the pole, it is given from the following relation:

19) Angle of arrival in one zero :

It is the angle with which the branch of the positive place arrives in the zeroes of the F(s) goes away from the pole, it is given from the following relation:

20) Like characterizing the points of intersection of the place of the roots with the imaginary axis :

It must be applied to the criterion of Routh characterizing therefore the k for which the system is to the stability limit and therefore the poles are on the imaginary axis, replacing this value of k in the characteristic equation the values of w are obtained .

21) singular Points of the place of the roots :

Points are stung that they represent multiple roots of the characteristic equation, that is that at the same time belong more coppers of the place. To the complete place of the roots they belong more to n m-1 the singular points.

The singular points in which are distinguished simple meet coppers pertaining to the same place and the multiple singular points in which meet pertaining coppers are to the positive place that to the place negative, such points are individualistic exclusively in the multiple poles or zeroes multiples of the function of transfer to open cycle F(s).

22) Relation in order to characterize the singular points :

_ uguagliando to zero the derivative of the equation characteristic find the point singular which to the aim to belong to the place must also satisfy la La draft number complex and therefore be of difficult solution, in its vece can use the 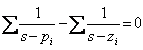which not characterize the point singular multiple, but this obtain immediately in how much coincide with the pole multiple and the zeroes multiple of the function of transfer to cycle open F(s). Also for this equation the points find to you must then satisfy .

23) Relation between the variety and coppers entering in the singular point :

If m are the variety that is the number of coppers entering in the point then these they divide the plan in 2m fields of equal amplitude.

24) Number of singular points between a pole and one zero contiguous ones :

There is always an equal number (0) of singular points between a pole and one zero contiguous ones.

25) contiguous Number of singular points between 2 poles or two zeroes :

There is always an uneven number (1) of singular points between a pole and one zero contiguous ones.

26) Towards of the arrows in the positive place and the place negative :

In a generalized manner the arrows are in the sense of the k increasing from -¥ a ¥ therefore in the place negative the arrows go from the zeroes (-¥) to the poles (0), while in the positive place they go from the poles (0) to zeroes ( ¥).

27) hydraulic Analogy :

For the positive place the poles like sources that therefore reject coppers of the place and the zeroes like pools can be considered that therefore attract coppers of the place.

28) Conditions on the system to open cycle affinchè the closed loop system is sure stable :

The poles and the zeroes to open cycle find all in the left semiplan, the barycentre is in the real axle shaft negative and the number of the asymptotes is smaller or to most equal to two.

Ended delays

29) When it is necessary to hold account of the delays ended in the real systems:

When the order of magnitude of the delay turns out greater of the greatest constant than time of the system.

30) characteristic Equation in presence of ended delays:

From the it is had that the poles are characterize to you from the characteristic equation

31) Conditions on the modules and on are made:

From the characteristic equation ricava and therefore they obtain the condition on the modules and the condition on fasi the .

32) Number of coppers of the place:

The number of coppers of the place is infinite being infinite the number of solutions of the important characteristic equation.

33) Typology of the points of the complete place of the roots for which it is had k=0:

From the condition on the modules one looks at that 2° the member is infinitely therefore the equality is verified if we find ourselves in the poles of the F(s) or s = -¥ .

34) Typology of the points of the complete place of the roots for which ¥ is had k ±= :

From the condition on the modules one looks at that 2° the member is the zero therefore equality is verified if we find ourselves in the zeroes of the F(s) or s = ¥ .

35) Simmetrie of the complete place of the roots :

Symmetry regarding the real axis in how much is had developing in series of Taylor obtains a polynomial algebrico.

36) Application of the criterion of Routh in the case of ended delays :

The characteristic equation cannot be applied in how much is important therefore has infinite solutions, the intersections with the imaginary axis can be determined in way approximated with one development in cut series of the exponential .

37) Asymptotes of the complete place :

The asymptotes are infinites and are all parallels to the axis of the abscissas and they intersect it in correspondence to the points .

38) Relation between k of the infinites the places to the intersection with the imaginary axis:

It is had that k the correspondent to the branch that intersects the imaginary axis with the smaller former is inferior to the k of the coppers that intersect the imaginary axis with greater former.

39) regarding Considerations the tracciamento approximated by means of development in series :

If the exponential is developed in series, other is not made that to add of the zeroes the whose type (real or complex) and number it depends on the order of the development to which is arrested to us, in particular looks at that if is arrested to us to an uneven order it has a zero real one which determines a place that the sign of the term of uneven order of elevated power is not compatible with the horizontal asymptotes moreover more imposes than to exchange the positive place with the negative. The number of the introduced zeroes moreover grows with the order of the development therefore is necessary to arrest itself to an order 2 or 4 to the maximum, also because for advanced equal powers braces of zeroes to negative real part are had.

40) Approximation of Padè :

Fratta concurs to approximate a polynomial with a function rations them, choosing the degree of the equal numerator to the degree of the denominator is found for the approximation of 1° order of the exponential 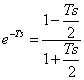while for the approximation of 2° the order 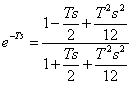famous that in both the cases obtains the turned out important to leave the excess poles-zeroes but in the case of approximation of 1° the order immutato it is necessary to exchange the positive place with the place negative.

41) Considerations on the stability in the case of systems to ended delays :

Draft of always unstable systems, in how much is present of the equivalent zeroes that are found in the positive semiplan and since to growing of k the place it is moved from the poles to cycle opened towards the zeroes to opened cycle, is had that necessarily và towards the instability.

42) Relation between poles to open cycle and poles :

A valid rule for systems with n-m ³ 2 asserts that the sum of the position of the poles to open cycle is equal to the sum of the position of the poles.

43) Contour of the roots :

In the case in which in a system beyond to the gain an other parameter like the position to of a pole can vary also, the obtained fictitious characteristic equation fixing k (equal to 1 is written normally) and collecting the terms in to , it is obtained therefore from which it can be varied to and finding the correspondent place of the roots.