The analysis in the state space

1) Variable of state:

They are the variable ones that must be created when an equation is had differentiates them of order n and it is wanted to be reduced to a system of n equations differentiates them of 1° degree, draft therefore of variable intermediate which not necessarily they correspond to measurable largenesses physically however more concur a description of the taken care of system regarding the transfer function. They constitute a carrier of state if the value of the escape in a time can be obtained

t > t₀famous that is the value of all the variable ones of state to time t₀ and the value of the incomes u the to the time t ³ t₀ .

 

2) Comparison between the approach by means of variable of state and the approach by means of the transfer function:

The approach by means of the transfer function is valid single in the case of linear and stationary system preferibilmente to a single income and a single variable escape while the approach by means of of set up state being in the dominion of the time, does not have these limitations.

3) Spazio of state:

It is the space in which the members of the state carrier are the aces coordinate to you.

4) Trajectory of state :

It is the described distance, in the space of state, from the free end of the carrier of state to varying of the time.

 

5) dynamic Equations for a system MIMO :

A system MIMO possesses various incomes and various escapes are described from the system dove:

To it is the matrix of system, or dynamics matrix

B is the matrix of income to the system, or matrix of forcing

C is the matrix of escape from the system

D is the matrix of direct logon exited income, in the real systems it is null

u is the income carrier

y is the escape carrier

x is the state carrier

 

6) Equations of state for a system SISO:

A system SISO possesses a single income and a single escape, is described from the system where stavolta b, u and c is carriers and matrices like were not had in systems MIMO.

 

7) Equations of state of the motor in controlled continuum flow on the armor:

Observing the equations , , , , it is observed that the only derived largenesses are_mthe (t) eed w_m(t) therefore are lend well to constitute the carrier of state, of the rest moreover the variable one of income of a motor in fed continuum flow on the armor is senz' other the tension of feeding of the armor and_to(t) while the variable one of escape is senz' other angular velocity w_m(t). Isolating to the first member of 4ª the equation and replacing in it the 2ª and also isolating to 1° the member of 3ª the equation and sostiutendo in it the 1ª it is reached the following equations of state 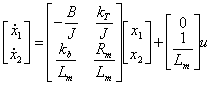where x₁ = w_m x₂ = i_m u = and_to y = w_m .

 

8) Matrix of transition of the state in the case of null income:

It is a matrix that in forcing absence concurs to pass from the carrier of state to time 0 to the carrier of state to the time t that is , its expression is obtained resolving by means of Laplace the equation differentiates them and then antitrasformandola, is had in fact and therefore from which antitransforming is had and therefore has that the matrix of transition of the state is . It can be demonstrated that it is esprimibile also in shape of exponential of matrix .

 

9) Property of the exponential of matrix :

to)                  

b)                 

c)                  

 

10) Property of the matrix of transition of the state :

to)      

b)      

c)      

 

11) Equation of transition of the state :

Transforming according to Laplace the and quindi is had, antitransforming this last one has and remembering that and that to the product in the domio of Laplace the convoluzione in the domio corresponds of the time ha , from it pu² to gain the answer of the system that turns out to be the sum of the free answer and the forced answer

 

12) Equation of transition of the state beginning from a time begins them whichever t₀ :

13) Answer to regimen y_r(t) :

It is the answer that is had for t®¥ that is t₀®-¥ that is .

 

14) transitory Answer y_t(t) :

where 2 integrals have been reduced to one changing the integration ends opportunely.

 

15) Calcolo of the autovalori of one matrix To:

The solutions of the characteristic equation must be found.

16) Dimensions of the nucleus of the matrix To:

where n it is the dimension of the matrix and r(a) the rank that is the number of lines or independent columns. This relation applied to (TolI) concurs to immediately estimate the geometric variety for a autovalore data and therefore to see less if the matrix to which it belongs can be diagonalizzata or.

17) Calcolo of the autovettori of one matrix To:

After to have found the autovalori, them one to the time in the matrix (To lIis replaced), it will be had necessarily that a line is cancelled and therefore uguagliando to zero the nucleus like span of or more carriers is characterized, in particular in the case that the algebrica variety is r, then the geometric variety, that is the number of the autovettori correspondents, is comprised between 1 and r, the matrix turns out diagonalizzabile single if the geometric variety is r.

18) Inverse of one T matrix:

is had where the added one has in the position (line r, column c) the determining one of the sottomatrice that is obtained eliminating the column r and line c, the all weighed one with the matrix of the alternated signs.

19) Methods for the calculation of the matrix of transition of stato jthe (t) = and^At :

to)       a T matrix of change of base constituted from the autovettori of the matrix can be characterized To that it transforms it in a L matrix on whose diagonal the autovalori of To which are present they go it multiplies to you for t and it elevates to you to and, obtaining in such a way the diagonal matrix and^Lt, finally is returned in the line of departure .

b)       the matrix must be antitransformed according to Laplace (â " To)^-1 .

20) canonical Shape of Jordan:

The matrices that cannot be diagonalizzate in how much posseggono autovalori whose algebrica variety is various from the geometric variety, can however to be capacities to diagonal shape "a nearly" said canonical shape of Jordan in which there are ovunque zeroes unless on the main diagonal where there are the blocks of Jordan everyone of which immediately has on the diagonal the multiple autovalore and diagonal over all 1.

 

21) Number of blocks of Jordan associates to you to every autovalore:

He is equal to the difference between the dimension n of the matrix To and the rank of the matrix (Tol₁I) or, more simply, he is equal to the geometric variety of the autovalore.

 

22) generalized Autovettore of order k:

Draft of a autovettore which it respects following the 2 property:

to)                   (To l₁I)^kv_k = 0

b)                  (To l₁I)^k-1v_k ¹ 0

 

23) Procedure for the calculation of and^At through the canonical shape of Jordan :

to)       the autovalori of the matrix are found To

b)       the autovettori for the having autovalori are estimated equal algebrica variety to the geometric variety

c)       for everyone of the other autovalori the autovettori are estimated generalize to you with the following procedure

1)       the number of chains of autovettori is characterized and therefore of blocks of Jordan it associates you to the single autovalore, such number is equal to the geometric variety of the autovalore that can be estimated as difference between the dimensions of the matrix To and the rank of the matrix (TolI)

2)       the length of one of the chains associated to the multiple autovalore is estimated calculating (TolI)ⁱ with i = 1,2,3,… sinchè the rank of the matrix obtained to the step k 1 is equal to the rank of the matrix obtained to the step k, the length of the chain is therefore k

3)       remembering the relations that define the autovettore generalizzato (To l₁I)^kv_k = 0 and (To l₁I)^k-1v_k ¹ 0 it calculates the carrier u_k pertaining to the nucleus of (TolI)^k and through the relazioni

v_k-1 = (To l₁I)v_k , v_k-2 = (To l₁I)v_k-1 , … , v₁ = (To l₁I)v₂ they obtain altri the ricorsivamente autovettori pertaining to the chain

4)       if to the point 2) the presence of an other chain has been found, of it is famous implicitly the length k and therefore the other autovettore of order k pertaining to the nucleus of the matrix (To l Iis found)^k and from it the other autovettori are obtained then ricorsivamente.

d)       all gather the autovettori find in one T matrix to you that door in the shape of Jordan

and)       ^Jt is estimatedand remembering that to every block of present Jordan on the diagonal a such block: is associated

f)        it is estimated and^At = T and^Jt T^-1.

 

24) Like passing from the equation of state to the transfer function :

The transformed ones of Laplace of the state equations are e in this last 1° term to 2° member are zero in how much for the transfer function consider the conditions begin them null x(0) = 0, is had quindi and quindi looks at therefore as the poles of the transfer function coincide with the autovalori of the dynamics matrix To.