Reflection and refraction of the flat waves

1) normal Incidence on a dielectric material:

In this case , in order to respect the conditions of continuity of the tangential members of the fields and and H a reflected wave is generated and a rifratta wave therefore the equations are e , projecting them on the aces obtain and also , replacing the 1ª in the 2ª characterizes said the relationship coefficient of reflection for normal incidence, analogous is reached the coefficient of reflection for the field H , it is observed that if the field and is the Concorde, the H field is discorde and viceversa. The transmission coefficients are e .

 

2) normal Incidence on a dissipative material:

We have inasmuch as for a flat wave that propaga in an average conductor it has while for the wave who propaga in the dielectric means it is ed therefore the reflection coefficient is being for the presence of g to the denominator that stretch to ¥ , is had that q_and @ 1 and with analogous considerations

q_H @the 1 therefore rifratto field and will be null while rifratto the H field will be the double quantity of that incident but decade esponenzialmente penetrating in dissipative means while in dielectric means a standing wave to which is established is associated some transport of power.

 

3) oblique Incidence on a dielectric material:

We suppose axis x horizontal, the outgoing axis y from the sheet and the directed axis z towards the bottom, therefore supposing that the wave incident belongs to the plan xz it has that the carrier b has member is along x who along z, for z=0 the equality between the tangential members of and door to the relation, equality that is had for every tern of fields on condition that the 3 esponenziali are equal that is that from this relation derives the law of Erone and the law of Snell let alone being the obvious equality between the speeds of phase along x of the 3 waves. In order to determine the reflection coefficients two locati carriers and_0h and and_0v in the orthogonal plan to b are considered , and_0h directed along y (…outgoing from the sheet) and and_0v in the direction, be a matter itself of a flat wave is had (…observes the reversal of the payers) moreover in analogous way writes the relative fields and and H you to the reflected wave and the rifratta wave. Projecting and and H along y the relations e are obtained , replacing the 1ª in the 2ª obtain which collecting h₂ and using , , door to the , is observed that q_Eh grows monotonous mente from the heat that it has for normal incidence until to the value 1 task for tangent incidence.

Projecting and and H along y the relations ed are obtained gaining and_0v is obtained that, with analogous considerations to those made for q_eh it is reduced to 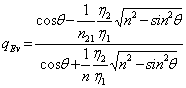. From the first famous expression that exists also a value of q said angle of Brewster for which q_Ev is cancelled, must be had that, elaborated door to the .

 

4) oblique Incidence on a dissipative material:

The fields incidents also have the customary expression , as the reflected fields , while for the rifratti fields it is necessary to hold account that and quindi , . For z = 0 the continuity of the tangential members of the fields must be had and therefore the equality of the exponents which is verified alone if that uguagliando the real coefficients gives and therefore in the dissipative means to is parallel to the axis z while equaling the imaginary coefficients is had that is still the law of Snell but extension that is not parallel to and therefore the wave in not dissipative means is not more uniform. From the equality a relative equation to the real part and a relative equation to the imaginary parts can be derived, from they it is possible to deduce and developing the following cases:

to)       Half with low dissipation:

e

therefore the phase vector is the same one that is had in the not dissipative means case while for the module of the attenuation carrier it is had that it is proporziona them to the conductivity and it depends also of the angle of incidence.

b)       Half conductor:

e

analogous to how much it was had in the case of uniform waves, the reason of that is that the rifratta wave propaga nearly orthogonally to the surface of discontinuity quindi to'// b' that it is just the definition of uniform wave.

It comes moreover defined the depth of penetration that is the distance from the surface of discontinuity to which the field it is reduced to of its value begins them for via of the conductivity, has and it is observed as it is infinitesimal for an ideal conductor (…g®¥), this is the reason for which the electromagnetic conductors are use you as screen and the necessary thickness diminishes to growing of the frequency.

In order to determine the reflection coefficients it is necessary to hold account that the 2° half the relation between is dissipative therefore and è with from the relationship between and₀ and H₀ deduces the stiffness of superficial wave which for a conductor only coincides with the intrinsic stiffness, the reflection coefficient can be scritto and famous that the power incident on a conductor comes nearly completely rifratta therefore the power from dissipated it is infinitesimal, also being dissipative.

 

5) Reflection total:

The refraction angle is 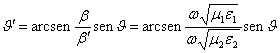clearly if (…that is if the speed of propagation in means 1 is minor who in means 2) does not have itself that an angle exists limit qsuch _L that 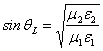and quindi that is the rifratta wave propaga in parallel with the discontinuity surface.

For q_L it is had that is maximum therefore the speed of phase of the rifratta wave is minimal but always greater of the speed of phase along x of the wave incident in how much has been supposed however if the rifratta wave is not uniform is had that it increases and therefore in such a way diminishes the speed of phase of the rifratta wave concurring the equality demanded from the conditions with the contour, after all is had that for q < q_L the rifratta wave is uniform while for q > q_L he is not uniform. As far as the power the rifratta wave is had that if we polarize the wave horizontally incident, also is polarized horizontally and the carrier of Poynting has one imaginary member along z₀ therefore not is power transport through the discontinuity surface but only parallel to it in how much one is had also real member along x₀ of the carrier of Poynting.