Flat waves

1) Characteristics of the waves in uniform means:

If the means are uniform it has that the refractive index is not function of the point and therefore and therefore the trajectories are rectilinear therefore the superficial ones of wave can be plans, spheres, cilindri, moreover being constant is had that the equations of the waves are to constant coefficients.

 

2) Characteristics of the flat waves in uniform means:

A wave with superficial of wave flat has expression, replacing it in the equation of the waves obtains 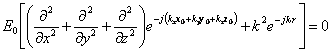, deriving it and remembering that the exponential is not never cancelled, the condition ma is gained, that is has uguaglianza the on which the following considerations are made:

to)       if and he is real then must be that it happens if the means are not dissipative (to= 0) or if to ^ b

b)       if and it is complex then must be .

In the more general shape however the wave can be written where is the factor of ampiezza and the carrier of attenuation to characterizes the plans equiampiezza while is the phase factor and the phase vector b characterizes the equiphase plans.

 

3) Characteristic of the flat waves uniforms and not uniforms in uniform means:

A uniform flat wave is characterized from plans equiampiezza coinciding with the equiphase plans, that it happens if to= 0 o to // b , the speed of phase in the direction of r₀ is not to confuse with the speed of propagation of the wave that is the speed of phase in the direction of b₀ and that naturally it is the minim in how much renders maximum the denominator. The value of the phase speed depends beyond that on the direction considered regarding b₀ also from the uniformità or less of the wave, in fact for a uniform wave (to= 0 or to//b) has while for a not uniform wave (to¹0) ha .

4) Relations between fields and propagation vector for a flat wave:

Replacing le expressions of the relative fields you to a flat wave e in the and using the vectorial relation con and si it obtains . An analogous result is obtained from the simplifying and reordering them ottengono e that is of the vectorial products between complex largenesses that are only simplified in the case of the uniform ondapiana (to= 0 or to//b) are obtained infatti

e

5) secondary Parameters:

a) k determines the transport and propagation characteristics

b) h determines the relationship between the amplitude of the electric field and the amplitude of the magnetic field

 

6) Considerations on the constant of propagation in the means case covered from currents of conduction but lacking in dielectric or magnetic dissipations:

The propagation constant has members 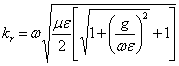e 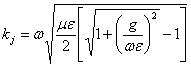from which famous that if the movement currents prevail on the conduction currents that is if is had then the means are behaved as a dielectric otherwise is behaved like a conductor , it is observed that in vhf the means stretch to behave themselves like a dielectric.

 

7) Considerations on the constant of propagation in the means case covered from currents of conduction but lacking in dielectric or magnetic dissipations:

Being |and''| < < and' in the real cases, from the , ottengono e in particular is observed that the means can become dissipative if w is much high one even if and'' it is infinitesimal.

 

8) intrinsic Stiffness for a uniform flat wave:

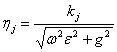The expression of the intrinsic stiffness is , considering the sun dissipations due to conductivity (and'' = 0) ottengono e therefore if the means are behaved from dielectric (we>> g) have while if it is behaved from conductor (g > >we) has and therefore it stretches to zero when the conductivity g stretches to infinite as it happens for a conductor.

 

 

9) Parameters of Stokes:

only 3 of the parameters of Stokes are independent in how much have these moreover last ones can also be expressed in function of the polarization parameters:

 

10) Sphere of Poincare:

To every point on such sphere a various polarization corresponds and viceversa, in particular it is had:

to)       to the points on Equator (c= 0) a linear polarization corresponds, as an example to the point of intersection between the sphere and the positive axle shaft of the x one horizontal linear polarization (y=0 corresponds) while to the point of intersection between the sphere and the axle shaft negative of the x vertical linear polarization corresponds one (y= 90°).

b)       to the North Pole (c= 45°) a left circular polarization corresponds while to the South Pole circular polarization corresponds one skillful.

c)       for the points of the hemisphere North has a left elliptic polarization while for the points of the hemisphere South one is had skillful elliptic polarization.