Electromagnetic irradiation
1) the function to climb of Green:
In electromagnetism a impulsive answer in the space in how
much is considered the sources has a sinusoidale course in the time
but they are null ovunque unless in the point r' in which they are
locate, it concurs to determine the produced electromagnetic
largenesses from the source in the points r of the space, in
particular the impulsive answer can be determined upgrades 
them carrier in this case coincides with the function
to climb of Green, or pu² to determine the field 
where stavolta the impulsive answer is the diadica function
of Green which is more complex dealing itself than a carrier. In
order to determine the function to climb of Green reference is made
the equation of the waves to climb (…projected on one of
the cartesian aces) in presence of space impulsive currents impresse 
of which the function to climb of Green is
solution.
The origin of the system of coordinates is the point where
the source is placed, if we consider the equation previous in the
external points to the sphere that comprises sources has 
from which dividend for r and taking the solution rG
is had whose solution is the sum of a
progressive wave and a regressive wave, this last one does not come
considered in how much physically does not have sense a wave that
collassa. Dividend for r finds the expression of the function to
climb of Green 
where coefficient C is found
integrating the equation 
on the
spherical volume of containing beamr the 0 sources, using the spherical coordinates and
dividend for r2 
is obtained that, carrying out the calculations door to 
that for r®0 becomes infinite but considering the infinites of
advanced order and becoming simpler 
is
obtained and therefore 
. After all whichever
of the space upgrades them carrier of a point is found with la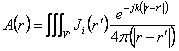 
extended to the single volume that contains
sources. In particular in the case of a impulsive source 
is found whose rotor in
spherical coordinates, become simpler holding account that 
for via of the axial symmetry of the source, gives
and is therefore always orthogonal to the
source, replacing it in 
the obtains 
therefore lies in a meridian that contains the
direction of sources. From the previous ones making 
the the induction field is obtained while col 
obtains the cancellation field.
2) Irradiation from sources of ended dimensions:
A source not more impulsive is considered but than ended
dimensions, a its point is taken like origin of the system of
coordinates, all the other points of the source to be distant r' from
it and R from the observation point p that instead tos be distant r
from the origin. The H field is gained from upgrades them
carrier To which the function is legacy to sources through the
impulsive answer…(to climb of Green) 
, clearly for r®0 of the terms within parenthesis considers alone 
while for r®¥ it is considered solo jb . The integral that obtains for the field to great
distance 
becomes simpler in how much if the
maximum D dimension of the source is much minor of the R distance
(…between a point of the source and the point p) is had
that the payer R0 @ r0 and therefore is
constant in the V' volume that encloses the source and can be carried
outside from the integral, like pure to the R denominator @ r while in the argument of the
exponential 
is replaced where 
is the payer in the direction that joins the origin
with the source point p' that it tos be distant r', after all
ha 
replacing itself in the
is obtained 
.
The carateristiche of the obtained fields are described from the cancellation condition:
.
3) electromagnetic Reciprocity:
The field produced from a monochromatic sourceTo 1 constituted from magnetic
currents impresse Jm1 and J
electrical workersi1 satisfies
the equations 
, 
, while for the analogous 2 sourceTo operating to the same frequency has 
, 
, multiplying
respective for H2 , and2 , - H1 , - and1 and adding
member to member obtains to 1° the member one amount that with
the solità vectorial identity it comes brought back to 
. Integrating to the 1° and 2° the member on one
volume V that contains the sources, to 1° the member can after
all be applied to the theorem of the divergence obtaining the theorem
of valid reciprocity for means isotropo 
and be
delineated where account has been kept that the J sourcesi1 and Jm1 is not null single in volume V1 that the source To 1 contains and analogous for the source To2. From the cancellation conditions
one deduces that the field to the infinite becomes infinitesimal
therefore integrating on one volume V that contains all the space
cancels the flow through the S surface that encloses it and the
equality of the reactions is had 
therefore
from which following can be deduced turn out to you:
to) considering absent the magnetic currents impresse in two thin dipoles that can be contained in two cylinders and decomposing the integral of volume in the series of an integral of surface that for the presence of J the current characterizes and of an integral of line that, for the presence of and, characterizes tension V, dividend for I1I2 obtains the equality of the mutual stiffnesses.
b) Applying the equality of the
reactions to a source To and a impulsive source of test space having 
is had that concurs
to gain the field produced from the source To in a point r.
4) Theorem of equivalence:
It is supposed of having a source To and a source of
unitary test that concurs to estimate the 
reaction, for the equality of the reactions it is also
equal tothe tA , the theorem of
reciprocity on a volume is considered but that contains all the space
ad.eccezione.del volume that contains the source To and is enclosed
from the S surfaceTo , in such a
way does not have the integral on the volume enclosed from STo , obtains 
from which through the vectorial relation 
dove 
is obtained
electrical worker is the superficial current while 
is magnetic the superficial current.
He has himself therefore that the field and nella 0 direction oft product gives it source To is the same product gives them to superficial currents equivalents that find on a surface that it encloses the source To.
