Dispersion
1) Speed of phase and group of a nearly monochromatic field:
Considering present single dominant term and0(s) in the development of Luneburg-Kline
and supposing that he is real, is had that the expression of the field
in function of the time and s is 
the j is in this case ignota therefore is
approximated to 1° the order by means of Taylor 
and replacing also 
is had
where the 1° exponential is relative to a periodic largeness with
pulsation w0 that propaga with speed of 
phasewhile the 2° exponential it modulates in the space
and the time the 1° exponential , and envelope is said, to it
corresponds one group velocity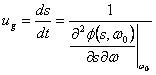 
.
2) Condition of equality between group and phase speed:
_ uguagliando speed of phase and group velocity di
gruppo and carry the denominator to the numerator of the member
opposite, obtain 
which be verify se 
, replace in it 
and
simplify ottiene 
and quindi 
which be verify alone if the refractive index di
rifrazione not depend from w.
3) Propagation of a not monochromatic field:
Carrying to frequency w 0 modulatedin having amplitude from a Gaussian impulse is considered
duration begins them 
therefore the expression
del field 
, writing the cosine in
exponential shape gains transformed of Fourier nel the point begins
them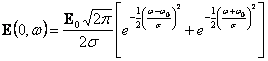 
cpstituita from two Gaussian bands of
amplitude 4s centered on -w0 and w0 .
The value of the transformed one of Fourier in the point s is
gained multiplying for 
, antitrasformandola
obtains 
it contains the eiconale function
which is incognito, however for the 1° integral pu² to be replaced
with a development in series arrested to 2° the order 
obtaining 
in which
carrying out the substitution and
subsequently 
e 
it is obtained, always for the 1° integral 
Analogous it is proceeded for the 2° integral where
stavolta for coherence with the previous positions for the eiconale
function the development is had 
where less
present on the derivative before it determines the definition of
largenesses conjugated regarding the previous ones and therefore
obtains, for the 2° integral 
. Replacing the
two it turns out to you finds to you and remembering that 
has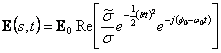 
.
4) Factor of amplitude:
therefore with increasing of the covered distance the amplitude of the field diminishes.
5) Factor of transport:
to it the shape of the impulse is tied that is still Gaussian but it changes its amplitude that is greater after the propagation. Factor of transport in how much in it is called is present is the time that the space and therefore the speed of the Gaussian impulse can be gained that is found is equal to the group velocity.
6) Duration of the impulse:
therefore with increasing of the covered distance
increases the duration of the impulse.
7) Difference between dissipative means and dispersive means:
It is had that the dissipative means transform electromagnetic energy in heat for Joule effect while dispersive means do not transform electromagnetic energy in an other shape of energy but simply it redistributes it in the space, therefore if we send to an impulse in dispersive means it it increases and it diminishes the amplitude of the field.
