Mathematical statistics
1) Esteem for intervals :
Draft of a having esteem the objective to characterize between all i values of c1 and c2 for which {c1 < X < 2c } = g, that one of minimal length.
2) Verification of the hypotheses statistics:
Branch of the theory of the decision based on the choice between 2 functions of distributions of probability is one.
H0 said base hypothesis
H1 said hypothesis alternative
3) Spazio of the events :
It is with of the possible events between which to choose, is indicated with M.
4) Spazio of marks them :
It is with of all the possible shapes of wave sended to the observer, is indicated with S.
5) Spazio of the observations :
It is with of all the possible ones marks them receipts, is indicated with Z.
6) Spazio of the decisions :
It is with of all the possible ones turns out you of the decision process, is indicated with D.
7) Rule of decision :
Draft of a determinist rule that associates to every observation one decision.
8) Error of 1° type in one binary decision after single observation :
An error of 1° type is had if the hypothesis H0 also comes rejected being true.
9) Error of 2° type in one binary decision after single observation :
An error of 2° type is had if the correct hypothesis is H1 but it turns out you of the experiment do not support the refusal of H0.
10) Criterion of the maximum verosimiglianza :
The decision rule chooses the event that has greater probability to have caused the observation.
11) Relationship of verosimiglianza :
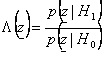
12) Criterion of Neyman - Person :
It characterizes a rule of decision that diminishes b , having fixed to .
13) Difference between parameter esteem and verification of the hypotheses :
The parameter esteem concurs through the observations on a single model to estimate of or more parameters while the verification of the hypotheses puts to comparison 2 models, that one of the null hypothesis and that one of the hypothesis alternative.
Accidental numbers
14) operating Definition of accidental number :
Sequence of accidental numbers is one turning out from a physical experiment
15) conceptual Definition of accidental number :
Sequence of variable aleatory is one i.i.d.
16) Modality for the generation of accidental numbers :
to) through tables
b) through congruenziali algorithms
17) Describe a generator of accidental numbers ricorsivo :
Part from a value begins them and si it obtains the successive value in function of the previous value.
18) Describe a generator of accidental numbers congruenziale :
The present value is based on the congruenza concept therefore them is legacy to the rest of the division for m of the previous value.
19) Method in order to generate accidental numbers with one given distribution through a calculating:
(u) is necessary to calculate the values of the Ffunction-1 for u = ui , being {u} one sequence of accidental numbers uniform.
20) Describe the method Mount Carl :
It is based on an accidental sampling and used as an example for the calculation of integrals, in practical N is carried out times an aleatory experiment and then it is estimated the average of all turns out obtained to you.
Theory of the esteem
21) Esteem of point :
Draft of one function of the observation x it è 
=
g(x)
22) Appraiser :
Draft of one function of carrier X constituted from all the observations x it è =
g(X)
23) Error of esteem :
It is the difference between the appraiser and the
incognito parameter q
cioè and = - q
24) Polarization of the appraiser:
Draft of the valor medium of the error of stima
b() = E(- q)
25) Variance of one appraiser :
It is the expected value of the square of the error of
esteem V() = E[ (-
E())2 ]
26) consisting Appraiser:
An appraiser is consisting if the esteem error stretches to 0 for N that stretches to infinite.
27) optimal Appraiser :
He is the appraiser who diminishes the quadratic error
medium e = E[ (- q)2 ]
28) Describe the esteem for intervals:
They come defined a brace of functions of the
observation1 = g 1 (X) e 2 = g 2 (X) which define a intervallo to
the inside of which the parameter q is contained with one probability g.
29) Objective of the esteem for intervals :
To diminish the length of the interval |1 - 2 | .