Questions of Theory of the aleatory phenomena
1) the statistical definitions of probability and their ties :
There are 4 possible definitions for the probability :
to) Axiomatic
The probability of the sure event is unitary.
The probability is a number comprised between 0 and 1.
The probability of an event that is sum of two not having events elements in common is the sum of the probabilities.
b) Frequency of repetition
The relative frequency of an event To is the relationship between the number of tests in which an element has itself like result of with To and the number of tests, when this last one stretches to ¥ , the relative frequency stretches to the probability.
c) Classic
The probability of an event To is the relationship between the number of the possible ones turns out to you favorable to the event To and the number total of the possible ones turns out to you. An improvement of the definition demands that the single ones turn out to you are equiprobabili.
d) Subjective, the probability is the price that an individual thinks fair to pay in order to receive 1 if the event verification.
2) the paradox of Bertrand :
It is a paradox legacy to the classic definition of
probability and that it puts it in crisis when the number of the
possible ones turns out to you it is limitless. One
circumference C of beam is had r, must be estimated the probability
that a selected rope AB to case has greater dimensions of the side 
of the registered equilateral triangle in the
circumference, will find therefore at least three various ones turns
out to you all just ones :
to) they consider the sun having ropes
the center to the inside of the beam circle 
, the
probability in terms classics can then be expressed like the
relationship between 2 areas, the area of the circle in which it can
fall the center of the rope and the area of C, the demanded
probability is worth ¼.
b) fixed an end of the rope, will find that the other end must be comprised within an equal angle to 1/3 of the perimeter of the circumference, therefore the probability in this case is 1/3.
c) the longer ropes are imagined
horizontal and with comprised former tra 
and 
, in this case find that the probability is
worth ½.
3) Theorems of the probability total and Bayes :
The Theorem of the probability total asserts that if a
partition of the sample space is had S in m events To1 ..., Tom and one B event defined on S then the probability of B is
given from the 
relation, is demonstrated writing
B as intersection with the sample space and therefore with the
partition To1 ..., Tom , decomposing and then using the
conditioned probability.
The Theorem of Bayes concurs for means of the theorem of
the probability total a posteriori to gain the probability of an event
pertaining to a partition To1 ...,
Tom of S knowing its a priori
probability, that is it is had 
. One gains
from the equality that gushes from the conditioned probability and
using the denominator the theorem of the probability total.
4) Independence statistics of variable events and aleatory :
Two events are said statistically independent if the
probability of the event intersection is equal to the product of the
probabilities of the single events 
. Two
variable aleatory ones instead are statistically independent if given
two with arbitrary To and B of values of X and Y respective, P{X is
had ? To, Y ? B} = P{X ? To} P{Y ? B}.
5) the conditioned probability : Definition and interpretation in terms of relative frequency and its property :
It is the probability that takes place an event To after
that event B has been taken place 
. In terms of relative frequency, the conditioned
probability of To B data is approximately equal to the relative
frequency with which the event To in the succession of tests is
introduced in which the B event is introduced.
6) repeated Tests and Binomial law :
Draft of tests that generate an equal sample space to the cartesian product of n sample spaces S being n the number of tests and S the sample space of the outcomes of the single test. The Bernoulliane tests are instead a particular case of the repeated tests, in how much the tests are between of independent they and 2 are alone turn out possible to you. It is spoken instead of generalized Bernoulliane tests if every test has r possible turns out to you.
The distribution of the successes is described from the
binomial law, in particular the number of the successes in a whichever
order is 
while the number of the successes
in a whichever order is 
.
7) the distribution function is defined and if of it they show the property :
The distribution function is apt to describe the
probability that an event is taken place is comprised in a data
interval, it is described from the 
terminology
therefore the function of distribution of one sure variable value x of
aleatory the X characterizes the probability that X have inferior
value to x. Have the following property :
to) it is comprised between 0 and 1 having to represent one probability.
b) it possesses of the jump
discontinuities which are continuous solos from right and whose value
is equal to the probability that variable aleatory the X assume value
x in issue 
.
c) 
d) If x1 < x2 then 
and) increasing function is one monotonous .
f) 
8) they are written and the property of the probability density are demonstrated :
The probability density is defined like the variable
derivative regarding aleatory the X of the function of distribution 
, therefore integrating it between 2 points x1 and x2 the probability is obtained that the X are
comprised in that interval ; from that it follows
that the integral extended to all the real axis must be worth 1.
9) the density of probability empiricist (histogram) and its interpretation in terms of relative frequency :
Axis x in intervals of D amplitude is subdivided , after which a experiment is executed n times and a height step is associated to every D interval proporziona them to the number of turns out to you that they fall in the interval, obtains therefore a histogram that it must be standardized so that the area from subtended it is unitary ; it stretches to the function of distribution for
n ®¥ and D®0.
10) the inequalities of Chebyschev and Markov : demonstrations and possible applications :
Both resolve to do to limit to determine inequalities that they give an idea on as is distributed the probability density.
The inequality of Chebyschev asserts that the
probability that variable aleatory the X assume external values to an
arbitrary interval (n-and ,
n and) is negligible if the
relationship s/and is sufficiently
small :
. It is obtained
setting up the solution like variance of two masses of probability.
The inequality of Markov instead asserts that the
probability that 
.
11) variable the aleatory exponential and its moments of order 1 and 2 :
Its density of probability is given from
. The moment of order 1 the moment of order 
2 is obtained from the while from 
12) variable aleatory c2 :
One important property is that the sum of the squares of n Gaussian independent standards is one c2 with n freedom degrees. A lot in statistics for the calculation of the variance of Gaussian functions to valor medium incognito is a used distribution, than it is found it are distributed like one c2 with n-1 freedom degrees where n in practical it coincides with the sample size.
13) variable aleatory the geometric one :
Its density of binomial probability somiglia a lot to one
less than a exponential 
. Its expected
value is 
that is obtained for comparison with
the derivative of the exponential series.
14) the law of the Great Numbers :
It asserts that the probability
that the relative frequency differs more from the probability in order
than and vale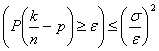 
. It is demonstrated simply applying the
inequality of Chebyschev and remembering that the number of the
successes is distributed one binomial with variance second npq.
15) the theorem of the limit centers them ; to give or more enunciates to you and to indicate one or more applications :
to) When the product npq®¥ the binomial one stretches to the Gaussian one.
b) the convoluzione of n Gaussian is still one Gaussian
c) the variable distribution of the sum of n aleatory stretches, to growing of n, one Gaussian. If the variable ones are continuous also the density Gaussian density approximates one.
d) If X1 ..., Xn is variable aleatory i.i.d. with valor medium h and variance s2 then for n®¥ the variable 
stretches to
one Gaussian standard.
16) the Poissoniana approximation of the Binomiale(Teorema di Poisson) enunciated and demonstration :
In the case of rare events that is of repeated tests for
which the succeeding probability of is smaller of 10%, it is convene
to approximate binomial with the Poissoniana the whose density of
probability is described from 
the , in which l it is the expected value
and it is worth np being n the number of tests and p succeeding
probability of. The theorem is demonstrated to leave from the
formula of Bernoulli taking advantage of that
n >> k and n >> np therefore for q = 1-p = and- p it has been able to use the
development of valid Taylor in the case of p infinitesimal.
Replacing 
is found.
17) the fundamental theorem : density of probability of one variable function of aleatory :
This theorem concurs to calculate the density of
probability of an aleatory variable function of leaving from the
acquaintance of the derivative of the function and of the density of
variable probability of the aleatory one of which it is function, 
is had:.
It is obtained taking 3 roots of the equation y=g(x) and writing 
the while this last one can finally be expressed
easily in terms of the x and observing that 
.
Replacing the theorem it is demonstrated.
18) the independence concept statistics between events, in one brace and one n-pla of variable aleatory:
Two variable aleatory ones are statistically independent if P{X £ x, Y £ y} = P{X £ x} P{Y £ y}.
19) Density of probabilities of one g(X two variable aleatory X Y and, function Y):
It is obtained from the derivative of 2° the order of the
function of combined distribution FXY is had :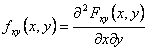 
20) coefficient and Correlation variable aleatory of correlation, case in which independence it coincides with the scorrelationship :
The coefficient of correlation of two variable aleatory X
and Y is worth 
where mXY is the
covarianza and is worth 
.
Two variable aleatory ones are said scorrelate if E[XY ] = E[X]E[Y ], relation that replaced in the covarianza extension that for variable scorrelate the covarianza and the coefficient of correlation is null.
Two variable aleatory ones are said independent > fXY = fX(x)fY(y).
You notice yourself that the scorrelationship indicates the absence of a linear tie between two variable while independence indicates the absence of whichever type of tie between the two variable ones, therefore independence implies scorrelationship but not viceversa unless in the case of variable aleatory Gaussian.
21) Transformation of one brace of variable aleatory ; to demonstrate the fundamental theorem and to describe the use of the variable member of the women's army auxiliary corps in order to obtain the function of variable density of one function of 2 aleatory ones:
If 2 aleatory variable functions of such Z and W are had
that Z = f(X, Y) e W = g(X, Y) then the fundamental
theorem describes like obtaining for means of the Jacobiano the
combined probability density function. 
is had, by means of opportune chosen of a variable member of the
women's army auxiliary corps can as an example be calculated the
density of variable probabilities of the sum of 2 aleatory ones.
22) Parlare about the linear transformations of an aleatory carrier and about the Gaussian multivaried one:
An aleatory carrier is a such carrier that one whichever combination of its members determines one variable aleatory Gaussian.
23) Ricavare the linear transformation that allows to render the members of medium a Gaussian aleatory carrier to valor null incorrelate and with assigned covarianza matrix:
24) the curve of regression of one variable aleatory on an other : property generates them, particular case of one brace of variable aleatory jointly Gaussian:
Draft of the integral that defines the expected value of Y
conditioned to X 
thought like function of j(x).
25) Life of a system ; reliability ; conditioned frequency of the breakdowns and its typical courses ; interpretation in terms of relative frequency :
The life of a system is the time interval that elapses
between the putting in function and the first breach, it is described
from variable aleatory the X, its function of distribution FX(t) is the out of order probability
that the system before the moment t while the inverse 
is the probability that the system functions to the
moment t and is called reliability.
the expected value of the life of the system is called
MTBF and exactly characterizes the medium time of operation without
breakdowns of a system. It comes finally described 
the dictates conditioned frequency of the breakdowns,
conditioned exactly to the fact that the system has worked until to
the time t. The possible courses of the conditioned frequency of
the breakdowns are : constant, with infantile
mortality, usury, to bathtub.
26) Tie between conditioned frequency of the breakdowns and reliability ; expected value of the rate the breakdowns :
dictates conditioned frequency of the breakdowns,
conditioned exactly to the fact that the system has worked until to
the time t. The expected value of the life of a system is equal
to the sum of the single reliabilities of the subsystems of which it
is made up.
27) conditioned density and Density of bivaried probability Gaussian its :
28) the concept of aleatory champion ; definition of the average of champion ; expected value and variance of the average of champion :
An aleatory champion is with of n variable i.i.d.
extracted from only variable aleatory a X, the average of champion or
average collection of samples is described from the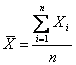 
relation, its expected value coincides with the expected
value h of the population
while its variance with the variance of the population but uniform for
n.
29) the density of variable probabilities of the sum of 2 aleatory ones in the general case and the case of indipendenza. :
In the independence case it is given from the convoluzione of the 2 variable functions of density of the two aleatory ones while the characteristic function is equal to the product of the two characteristic functions.
30) quadratic Convergence in average and convergence in probability : definitions and connection between the two convergences :
The quadratic convergence in average is given from the 
relation.
The convergence in probability instead is given from the
relation 
.
The relation between the two is that if Xn converges then to quadratic c in average it converges to c in probability as it is obtained applying the inequality of Markov.
31) variable aleatory c2 : definition and use statistics :
The property of c2 are following :
to) If X are one c2 with m degrees of freedom then Z = X Y are one c2 with m n freedom degrees.
b) the sum of the squares of n Gaussian independent standards is one c2 with n freedom degrees.
c) One c2 with 2 degrees of freedom is one exponential density.
32) Distribution of the average and the variance collection of samples :
The medium collection of samples is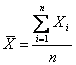
it has equal expected value h
to that one of the population and variance 
.
The variance collection of samples is 
, its
expected value turns out is equal to the variance of the 
population. An important result is that variable the
aleatory 
is distributed like one c2 with n-1
freedom degrees. For values it elevates you of n the medium
collection of samples follows the normal law approximately.
33) binary Decision with single observation : concepts generate them and test of Neyman - Pearson, this last one with relative demonstration :
A binary decision when in the space of it marks them S are 2 marks them, to everyone of they is had is associated one of the 2 partitions of the space of the Z observations and must is taken one of 2 decisions d0 or d1 . The error of 1° type is the probability that marks them was S0 but it comes erroneously taken decision d1 , is indicated with to and it is said level of significance of the test. The error of 2° type is the probability that marks them was S1 but it comes erroneously taken decision d0 , is indicated with b and its inverse P = 1 - b power of the test is said.
34) Theory of the decision and criterion of Neyman - Pearson :
It is proposed to share the space of the observations so
as to to associate of the elements to the space of the decisions.
The criterion of Neyman Pearson leads to the location of a
decision rule that diminishes b having fixed to.
In short one applies to the method of the multipliers of
Lagrange trying between all the regions for which the level of
significance of the test is that fixed one to0 , that one that it maximizes
the power of the test b .
One finds that the verosimiglianza relationship is greater of
the multiplier l chooses d1 otherwise chooses d0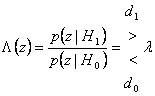 
35) axiomatic Theory : Illustrious the difference between the esteem of Bayes and that one not of Bayes ; it is exemplified to the case of measures affette from errors :
In the approach classic the parameter q of distribution fX(x,q) is seen like one constant, incognito but determinist. In statistics of Bayes the incognito parameter q is seen like one realization of one variable aleatory F .
36) Generation of numbers pseudo - accidental with assigned distribution leaving from numbers pseudo - accidental uniforms in [ 0.1 ] :
If X are one variable aleatory one with distribution F(x) then U = F(x) it is uniform distributed in (0.1) with F(x) distribution enough therefore to apply the F-1(u) to every u pertaining to the sequence of accidental numbers with uniform distribution in (0.1).
37) Describe the method Mount Carl :
It is a method based on an accidental sampling, in short an aleatory experiment is repeated n times and it is estimated the average of turns out obtained to you. The method is used is for applications statistics that for determinist applications. It is used as an example in the calculation of integrals for which the two following methods are available :
to) Through riscalamenti it is made in way to integrate between 0 and 1. The integral turns out to be the expected value of the function g applied to a variable uniform in (0.1) extracting therefore some champions, the integral is characterized from their medium collection of samples.
b) 2 variable uniforms are generated in (0,1) u and v and for every value of the u it is controlled if v are smaller of g(u). The incognito integral therefore is given from the relationship between the number of tests in which v £ g(ui) and the number of tests.
38) Construction of appraisers with the method of the moments :
The method of the moments consists in equaling the moments of the function of famous distribution with the moments estimates to you
39) Esteem of parameter with the method of the maximum verosimiglianza. Property of the appraisers of maximum verosimiglianza :
The method of the maximum verosimiglianza is based on taking that value of q that more verosimilmente it has given place to the data observes to you. That in short happens deriving regarding the incognito parameter the verosimiglianza function that is the density of the aleatory carrier of i champions f(x , q) thought like function of q. They are appraisers who for small champions have insufficient performances, turn out in fact polarizes to you and having great variance, with increasing of the number of the champions they decrease is the polarization that the variance and the function of distribution stretches to the Gaussian one.
40) statistics of Pearson and the test of the goodness of adaptation between a theoretical law and a law empiricist :
The test has the scope to establish if a data theoretical
model adapted to the data effectively is found to you, or if two
sets of data it experiences them they can be described from the
same model. The base hypothesis is that the probabilities of m
events Toi are equal to m given
values p0i . The
statistics that uses itself is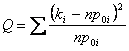 
obtained
considering that the binomial one can be approximated from one normal.
41) statistics of Pearson and the test of c2 :
Statistics of the test of Pearson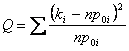
badly lend itself to the location of percentile q1- then for values
elevates to you of n the distribution of statistics comes approximated
with one c2 with m-1 freedom degrees since the tie is
prevailed 
, the base hypothesis comes rejected if
the value of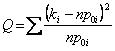 
statistics is greater of percentile c21-to(m-1).
42) the least-squares method : determinist interpretation, statistics and predittiva. :
A function j (x) must be characterizedthat better adapted
second a criterion predefined to with of given points. The
method consists in determining m parameters li of the model j(x) so that it turns out minimal
the quadratic error 
.
Determinist interpretation :
Braces (xi , yi) are braces of famous numbers.
Supposing to approximate with a straight one y=a bx in order to determine to and b other does not
have to be made that to diminish the quadratic error that it is obtained uguagliando to 0 the derivatives
respect to to and regarding b.
Interpretation statistics :
Abscissas x are famous numbers, while the formers y are the aleatory values observe you of n variable Y of expected value E[Y] = j(the xi).
Predittiva interpretation :
It is the abscissas that the formers are the values observe you of variable aleatory.