Analysis of Fourier

1) Series of Fourier associated to one periodic function :

essendo e

such series is convergent > the periodic function integranda is limited

 

2) exponential Shape of the series of Fourier :

con

 

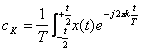
3) Theorem of Parseval :

For the energy of it marks them periodic in a T period, that is for its medium power it is worth the equality

 

4) Write the function envelope of the coefficients of Fourier of a pulse train :

 

5) Meant of the transformed one of Fourier :

It concurs to write the series of Fourier also for functions that are not periodic considering the limit for the T period that stretches to ¥ .

 

6) It marks them of energy :

Draft of marks them x(t) such that

 

7) Convoluzione and its property:

A convoluzione is the function turning out from the product of 2 functions g(t) = f(t)*h(t)

to)    f(t)*h(t) = h(t)*f(t)

b)    [ f(t)*h(t)]*k(t) = f(t)*[h(t)*k(t) ]

 

8) Property of the integral of Fourier :

to)    Translation

b)    Convoluzione

c)    Symmetry

d)    Linearity

and)    Dualità

f)     Scalatura

g)    Coniugio

h)    Derivation

i)      Integration

 

9) characteristic Function:

The characteristic function j(w) of one variable aleatory X whose density of probability is f_X(x), is defined like

alternatively like the variable expected value of aleatory and^jwXthe , it assumes the its equal maximum value to 1 in the origin.

 

10) Function generatrix of moments of one variable aleatory X:

 

11) Second characteristic function of one variable aleatory X:

 

12) Second function generatrix of moments of one variable aleatory X:

13) Cumulante l_n of one variable aleatory X:

Draft of the derivative n_esima of the second function generatrix of the moments estimated in point s = 0.