Theory of the functions of one variable complex
1) convergent Succession :
The succession {zn} is said convergent to the limit z if " and > 0 $ a N(indexand) to leave from which all the elements zn of the succession satisfy the inequality |z - zn| < and for n > N(and).
2) necessary and sufficient Condition so that {zn} converges is that they converge simultaneously {ton} and {bn}:
3) limited Succession :
A succession is limited if $ one such positive number M that " element zn ? {zn} it is worth the inequality |zn| < M
4) From every limited succession one can be extracted convergent subsuccession :
If {zn} it is limited then they are also SKing zn e SIm zn therefore choosing an opportune one nk is had that King znk Im znk converges.
5) Criterion of Cauchy :
The succession {zn} is convergent > " and > 0 a N(index can be foundand) such that |zn - zm| < and for n,m ³N(and)
If zn it is convergent, for 2) the real successions to n must converge also and bn and therefore $ N 1 can on they be applied the criterion of Cauchy and be said that " and >0(and) such that " n,m > N1(and) is had that |ton - tom| < and / 2 and that
" and > 0 $ N2(and) such that " n,m > N2(and) are had that |bn - bm| < and / 2. Choosing N(and) = max(N1(and), N2(and)) it is had that for the n, m greater of N(and) is had |zn - zm| < and .
? It can be observed that the module |zn - zm| is sure greater of the module of the difference of the real parts or the module of the difference of the imaginary parts, therefore ha |ton - tom| < and e |bn - bm| < and and therefore {ton} and {tom} is convergent successions and therefore also {zn}.
6) indefinitely increasing Succession :
A succession {zn} says indefinitely increasing if " positive number R exists a N index to leave from which the terms of the succession satisfy the condition |zn| > R for n ³ N.
7) Point to the infinite :
It is the point which every increasing succession converges indefinitely.
8) Definition of point to the infinite by means of the stereographic projection:
Images that the complex plan corresponds with the plan xy of R3 and considers circumference of beam unitary centered in origin, well transformation T associates to every point of plan complex point of sphere that turns out from the intersection of the same sphere with combining of the point with the North Pole, such intersection turns out in North Pole if point is external to sphere while South Pole is in if point is inner to sphere, well if we have a succession of points that on the sphere stretches to the North Pole, then the inverse transformation T-1 stretches to the point to the infinite.
9) inner Point :
A point z says inner point of together and if its completely contained in together exists around and
10) With opened :
It is a constituted entirety alone inner points.
11) With connected :
It is with in which taken 2 whichever pertaining points to it, they can be joined by means of one poligonale whose points are contained in with same.
12) Dominion :
Open and connected draft of with.
13) Point of frontier :
A point z says point of frontier for and if in every its around there are it is stung of together and that of its complementary one.
14) closed Dominion :
Draft of the union of a dominion with its is aimed of frontier.
15) limited Dominion :
Draft of a dominion situated completely to the inside of one circumference of ended beam.
16) Limit of one complex function:
Number w0 says value limit of the function f(z) in point z0 if " and > 0 a d can be found > 0 such that for all the points z that they satisfy condition 0 < | z - z0 | < d it is worth the disuguaglianza |f(z) - w0| < and .
17) Continuity of one complex function:
The function f(z) is continuous in point z0 if " and > 0 a d can be found > 0 such that for all the points z that they satisfy the condizione | z - z0 | < d it is worth the disuguaglianza |f(z) - f(z0)| < and .
18) Derivative of function of one variable complex :
If this limit exists then 
ended the
limit it says derived of the function f(z) regarding the variable
complex z in point z0 .
19) geometric Interpretation of the complex derivative :
Also in the complex case the derivative is seen like
relationship between the variation in the D imagew and the variation in
the D dominionz, to
the limit for this last one that stretches to 0, not curing to us of
the fact that is the dominion that the image is bidimensional, has
therefore 
that is draft of a complex number
whose argument to is given
from the difference between the argument of the numerator and the
argument of the denominator but these arguments when Dz®0 is equal to the tangents to the respective curves in
the image and the dominion and that is is par to the included
angle between the real axis and the carrier Dz or Dw 
this difference is
same for the every one other point passing for z0 . This property is said of
conservation of the angles.
The property of the linear expansion, is obtained instead
making the module of 
the from which it finds
that 
and therefore k characterizes the
coefficient of scale of the similitudine.
20) Definition of differentiable function in complex sense:
f(z) he is differentiable in z0 if it respects the following equation:
being 
e 
.
21) f it is analytics in z0 > f is differentiable in
z0 and it is had 
:
Deriva directly from the function definition analytics
?
Enough to take the differenziabilità definition 
to carry f(z0) to the first member and to divide then for (z-z0) taking advantage of
that is had the derivabilità definition which
is only had in the case that f is analytics.
22)Se the function f(z) = u(x, y) the v(x, y) is derivabile in point z0 = x0 iy0 then in point (x0 , y0) exists the partial derivatives of the functions u(x, y) and v(x, y) regarding variable x and y and the sussiste the relation of Cauchy - Riemann
a) ux = vy b) uy = - vx
For definition a function is analytics if he is
differentiable and 
but of the rest is
had that 
therefore 
and analogous 
replacing in the previous one
the conditions of Cauchy-Riemann are obtained just.
23) Function analytics or olomorfa or to regulate:
The function f(z) says analytics, olomorfa or to regulate if he is derivabile in all the points of the dominion and its derivative is continuous.
24) f it is analytics > the partial derivatives of the functions u(x, y) and v(x, y) they exist, they are continuous and for they they are worth the conditions of Cauchy - Riemann:
25) Theorem of Gouisal:
If f it is opened analytics on with then f ? There
26) entire Function :
Draft of one olomorfa function in all C.
27) consistent Application :
Draft of the transformation of around of point z0 in around of point w0 carried out from the function analytics
w = f(z), having in the point zthe 0 property of conservation of the angles and costanza of the linear expansion.
28) Shape differentiates to delineate them :
w = A(x, y)dx B(x, y) dy B, complex continuous on W .
29) Theorem of Gauss - Green :
It is open W (limited) and ¶at times such regular W that w ? There (W) ? C(W)
30) Shape differentiates them sluice :
A shape differentiates them w says sluice if he is exact and derivabile, for a shape differentiates them sluice is had Toy = Bx .
31) If W is a simply connected dominion,
w it is chiusa > w is exact
If w it is sluice then Rot F = 0 that
is Toy = Bx therefore applying the theorem of
Gauss Green to the contrary has 
and this last
one is one of the definitions of w exact that is that its integral along a closed distance
is null.
? If w it is exact then it admits a function upgrades them such U that To = Ux and B=Uy deriving before the respect to y and the second respect to x and taking advantage of the theorem of Schwarz on the equality of the mixed derivatives, is had
Toy = Uxy = Uyx = Bx and therefore is had that w it is sluice.
32) Formula of Green in the complex case :
Being 
it is had that
con A=f e B = if therefore is had to leave
from the valid result in the real field 
33) closed Contour :
Draft of one curve regular sluice at times deprives of car intersections.
34) Theorem of Cauchy :
In a simply connected dominion the extended integral of f(z) is defined a function analytics f(z) to every closed contour G, completely contained in the G dominion, is equal to 0.
having applied the conditions of Cauchy Riemann since f it
is analytics.
35) Second formulation of the theorem of Cauchy :
If the function f(z) is analytics in a simply connected dominion limited a regular contour at times C and is continuous in the closed dominion G the integral of the extended function f(z) to the frontier of the G dominion he is equal to zero.
36) Integrals of Fresnel :
Integrating 
on a closed circuit, the
2 real integrals are obtained 
37) integral Formula of Cauchy :
If f(z) it is long analytics within and frontier C of
one region simply connected R 
You notice yourself in fact that f(z) it is
analytics ovunque except that in z = to, therefore the integral is
independent from the closed circuit that encloses to, that is the
integral along C is equal to the integral carried out along a beam
circumference and centered
in to that is 
, a parametrizzazione for G è z = to and and q and therefore dz = and and the q replacing are obtained
and passing to the limit for and ® 0 and
isolating f(a) obtains the thesis.
38) Theorem of the valor medium :
The value of f is f olomorfa in the dominion To in a point of To is
equal to the average of the values of f on one any circumference
centered in that contained point and, with to its inside, in A
: 
It is demonstrated to leave from the formula of
Cauchy where admitting that z = to king the q is a
parametrizzazione of circle C ha dz = ire qthe and replacing in the
integral it is obtained 
.
39) Principle of the maximum module:
It is f(z) analytics within and long one simple line sluice C the maximum of |f(z)| it is found less along C than f(z) it is not one constant.
The function is continuous on a compact one therefore
admits a maximum, supposes for absurdity that such maximum is assumed
in a point to inside to the dominion, applying the theorem of the
average on a circle centered in to will have 
therefore the value of the f(a) is just M and is equal to the
valor medium, but for the points of the circumference it is had to
have itself |f(a)| > |f(a re the q)| then medium value M cannot be caught up and this
implies that it was an absurdity and that therefore the maximum comes
assumed on the edge of the circle. Evidently therefore if the
maximum is inner to the dominion, the function cannot that to be
constant to the inside of the same one, if therefore is not then the
function assumes the maximum on the edge of together.
We have in such a way demonstrated that the function is constant to the inside of the circle of center to, in order to extend the result to all the dominion, takes a whichever point and it is combined with a line to to, dopodichè a point is taken on this line that is next to the edge of the first circle and it is assumed like center of the new circle on which repeating the previous considerations.
40) Corollario of the Principle of the maximum :
It is To olomorfa a limited dominion and f in To, it continues in To , and not costante the function z® |f(z)| it assumes the maximum on the frontier of To.
41) Theorem of the minimal module:
It is f(z) analytics within and along the simple line sluice C and is f(z) ¹ 0 within C |f(z)| it assumes its long minimum C.
f(z) it is analytics within C and since it does not have
zeroes in such dominion it follows specularly that 
also is analytics within C therefore being in the
conditions of validity of the theorem of the maximum such module
function can only admit the maximum on frontier C and therefore |f(z)| it can only assume the minimum on frontier C.
42) Appraisal of the derivative of an integral employee from a parameter:
The derivative of the integral is equal to the integral of the derived function integranda regarding the parameter.
43) Lemma of derivation under the sign of integral :
It is To a dominion and G an arc of oriented curve, and j a defined function and continues on G the largeness 
defines in To \ G a olomorfa
function, and its derivative has the expression
moreover f it possesses derived of every order
and 
is had.
Part from the integral of Cauchy 
,
the function integranda is analytics regarding z and its partial
derivative is 
therefore remembering that the
integral of Cauchy is an integral employee from the parameter z, is
had that its derivative is equal to the integral of the derivative
regarding the parameter of the function integranda.
44) Theorem of Taylor :
It is f is analytics to the inside of circle C with
center in to the series
of Taylor of f in the point to : 
converges to f(z).
It is z an inner point to C and one circle C 1is constructed which it
encloses z but it is contained in C and both the circles are center to you in to. The value of f(z)
therefore is given from the integral formula of Cauchy 
but of the rest it is had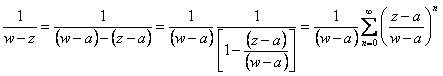 
on
condition that it is the smaller relationship of 1 ossia |z-a| < |w-a| therefore to the inside of circle C1 . To this point it is
multiplied for f(w)/2pi,
integral one on C1 obtaining therefore to the first member the f(z) while to
the 2° membro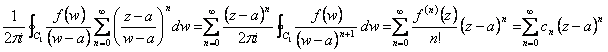 
45) Oneness of the development in series of powers :
It is f olomorfa in the dominion To z0 ? To,e it
is had, in around of z0 
46) Inequality of Cauchy :
If f(z) it is long analytics within and the beam circle C
r and center in z = to, 
being
M : |f(z)| < M
Part from the integral formula of the
derivative of Cauchy 
from which taking to the
module and maggiorando the curvilinear integral with the length of
circumference 2pr
multiplied for maximum M task from the function on the circumference
is obtained.
47) Theorem of Liouville :
If for all the points of entire the slowly complex one, f(z) it is analytics and limited f(z) he is constant.
It is obtained from the inequality of Cauchy taking n =
1 ha 
and being the
null derivative before " z
it follows that the function must be constant.
48) fundamental Theorem of algebra :
Every polynomial of degree n ³ 1 it possesses at least one zero in the complex plan.
We admit for absurdity that polynomial the P(z) does not
have zeroes , therefore 
it is analytics for
whichever z and it turns out also to be limited in module per z® ¥ therefore for the theorem of
Liouville the function must be constant, but a polynomial it cannot be
constant being of degree n ³1 and therefore the polynomial is fallen in contradiction,
consequently must admit a zero at least, will be demonstrated then
that the n° of the zeroes it is exactly n.
49) Theorem of Laurent :
If f(z) it is analytics within and long 2 circles concentrate of beam respective R 1and 2 Rand center to us in to
con 
DEMONSTRATION OF THE EXISTENCE
We characterize 2 circumferences of beam R1 and contained2 R <R a 1 to the inside of the circular crown and inner
point z to the 2 circumferences, then the value of the function in
this point z is given from the formula of Cauchy, 
for 1° the term is reasoned therefore as for the
series of Taylor characterizing the sum of a convergent series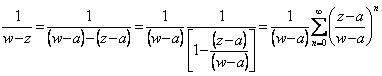 
therefore has 
with 
.
Collecting analogous for 2° the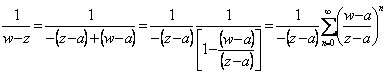 
member 
is obtained
con 
. Since to the inside of the circular
crown the function is analytics, the theorem of Cauchy can be applied and therefore the
integral is independent from the particular distance, follows some
that the 2 solutions can be grouped in 
with 
.
DEMONSTRATION OF THE UNICITA'
It is assumed of having 2 series that differ for a single coefficient, multiplies both for (z-z0)- m-1 and if of ago the integral along a circumference comprised in the having ring of olomorfia and center in z0 , replacing to this point z = Kingthe q finds a 0 integral that it is worth if n¹m while it is worth 2pif n=m, after all in every development there is a single not null term and is equal for the two series that therefore coincides.
50) dismissable Singolarità :
If a function to sol a value is not defined in z = to, but
it exists 
says that z = to dismissable singolarità
is one.
51) If f(z) it is limited analytics and in a dominion that excludes z0 , then point z0 is a dismissable singular point :
Affinchè z0 is a dismissable point singular, the coefficients of the main part of the series of laurent must be all null ones, that it is demonstrated writing cn in terms of the integral and carrying out the customary maggiorazioni holding account that the function is limited that is!f(z)| < M, replacing then (z â " z0) = kingthe q and making the limit for r®0 obtains 0 like intentional.
52) Pole :
If a function to sol a value has a pole in z = to, 
and the number of present terms in the main part of the series
of Laurent corresponds to the order of the pole.
53) If point z0 is a pole of the function analytics f(z) for z®z0 the module of the function f(z) grows infinitely, independently from the way in which the point z it stretches to point z0 :
Enough to write the development of Laurent to leave
exactly from the term â?"m supposing a pole of order m, collecting in
main part (z-z0)- m have 
limited
where j the (z) is analytics
and in around of z0 and
therefore term (z-z0)- m it commands and it pushes towards
infinite the f(z) for z®z0 .
54) If a function f(z), analytics in around of a its singular point isolated z0 grows infinitely in module independently from the way in which the point z point z 0 stretches to point z 0 it is a pole of the function f(z) :
The function is considered 
which
stretches to 0 for z®z0 therefore is limited and
therefore for it z0 are a
dismissable singolarità and can therefore 
be
written where j(z) is a
function such analytics that j(z0) ¹0 has therefore that 
that is the definition of pole of order m.
55) essential Singolarità :
If f(z) every singolarità is a function to sol a value that is not of a pole of a zero is an essential singolarità, in particular if z = to the main part of the development of Laurent is an essential singolarità then has a number infinitely of terms.
56) meromorfa Function :
A function says meromorfa if it is analytics in all the plan with the exception of an ended number of poles.
57) Theorem di Casorati - Weierstrass :
For every and> 0 in whichever around of essential a singular point z0 of the function f(z) a point z 1 in which the value of the function exists at least f(z) it differs less from a complex number arbitrarily assigned B in order than and.
We suppose for absurdity that exists around ofz 0 in which it is
taken place that 
, then the 
function is limited and therefore point z0 is a dismissable singular point of y
che therefore for the
previous theorem, can be written come 
and
gaining f(z) from the 
is obtained but if m=0 this development
characterizes a regular point for f(z) otherwise characterizes a pole
of order m and not one essential singolarità as the theorem demanded.