Complex series
Numerical Series
1) convergent Series :
The 
series says convergent if the
succession {S n} ofits
partial sums is convergent, in such case the S limit of the succession
{Sn} says sum of the series .
2) Rest n-esimo of the series:
Draft of the series 
.
3) Criterion of convergence of Cauchy :
The series is convergent > " and > 0 a N index can be found such that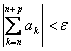 
per n ³N.
4) absolutely convergent Series :
If the series to real terms 
then is
convergent also the series that in this case is said
absolutely convergent.
5) Criterion of convergence of Of Alembert :
The series is convergent if,
beginning from a N index, is worth the relation 
" n ³ N.
6) Criterion of convergence of Cauchy :
The series is convergent if,
beginning from a N index, is worth the relation 
" n ³ N.
Series of functions
7) punctual Convergence :
The series of functions 
says convergent
in its dominion if the numerical series to relative it converges " z that is if " z and for every positive number and a N index can be found such
that 
for n > N .
8) uniform Convergence :
The series of functions uniform says
convergent in its dominion if the numerical series to relative it
converges " z that is if " positive number and can be found a N(indexand) such that " n > N(and), every for z pertaining to the
dominion.
9) Criterion of Weierstrass of convergence total:
If in a dominion the modules of the terms of the series of
functions are increased ovunque from the terms of
an absolutely convergent numerical series the series it converges uniform in
its dominion.
10) Criterion of Cauchy :
Necessary and sufficient condition for the uniform
convergence of the series is that " and > 0 a N(existsand)
such that the 
relation is verified simultaneously
in all the points of the dominion for n ³ N and " m.
11) Theorem of Weierstrass on the property of the uniform convergent series :
If the functions un(z) are continuous in u dominion and if the series converges uniform in this dominion to the function
f(z) also f(z) it is
continuous in the same dominion.
12) Theorem of Abel or Cauchy - Hadamard:
If the series of powers 
converges
in a point z1 ¹ z0 , it converges absolutely also in
a such point z that |z-z0| < |z1 - z0| ; moreover the series converges uniform
in every circle |z-z0| £ r of beam r < |z1 - z0|.
Being the convergent series in z1 then its terms stretch to the zero for n®¥ therefore general term can that is be increased from one
constant M 
and therefore 
is had but we are interested to see if the series for a
such point converges absolutely z that |z-z0|<|z1 - z0| therefore we take the module
of the series of 
powers but this
last one is a geometric series of reason q<1 and therefore the given
series is convergent therefore for the criterion of the comparison
converges absolutely. In order to demonstrate the uniform
convergence the criterion of Weierstrass is used that previews the
maggiorazione with a convergent numerical series which as an example
it can 
be r < |z1 - z0| .
13) convergent series of powers to f(z)
Is one in the circle of convergence D(z0 , R)
f(z) is analytics and f ' (z) = 
14) Theorem of the passage of the limit under the sign of integral:
Given one series of uniform convergent
continuous functions and to u(z) in a D dominion
" at times contained regular G curve in D is had 
It observes itself that the difference between
the two integrandi is equal to the rest n-esimo and being the
convergent series uniform, can that is be increased 
where L is the length of the curve along which integral,
therefore 
is had and therefore there is the
equality between the two terms.