Theory of the residual ones
1) Residual :
Draft of the coefficient to-1 of the series of Laurent 
2) Formula in order to calculate the residual one in z = to when to it is a simple pole:
It is obtained to leave from the development in series of Laurent, multiplying for (z-a) and making the limit all the terms are cancelled ad.eccezione.del coefficient c-1 .
3) Formula in order to calculate the residual one in z =
to when to it is a simple pole and f(z) is a relationship of
functions 
:
The f(z) the denominator has a pole that is has a zero in
to and therefore he can be written in series of Taylor 
and observing the function he finds that the coefficient
of 
is just 
4) Formula in order to calculate the residual one in z = to when to it is a pole of order m:
If to the series of Laurent of f(z) is a pole of order m
then it is : 
multiplying
per (z-a)m obtains one series
of Taylor deriving which m-1 times and making the limit for z®to is obtained to-1 in fact 
from which the demanded
formula.
5) Theorem of the residual ones :
It is f(z) a function to sol a value and analytics to
the inside and on the simple line made sluice C eccezion for the
singolarità to, b, c... to the inside of C that residual data have
giveto -1 , b-1 , c-1 .... 
He is sufficient to take for every singolarità a
contained in C and centered circumference in the same singolarità,
and to observe that 
and to observe
that everyone of the integrals to second member can be simply
extrapolated from the coefficient to-1 of the series of Laurent, in fact is had 
.
6) Residual to the infinite :
Residual of the function the analytics f(z) in the point
z = ¥ it is the equal
complex to the value of the integral
7) If f(z) it is a function analytics in all the complex plan with the exception of an ended number of singular points isolates to you between which z = ¥ the sum of the residual ones is zero.
8) Lemma di Jordan :
If the function f(z) is analytics in all the advanced
semiplan with the exception of an ended number of singular points it
isolates to you and it stretches to zero for |z| ® ¥ uniform respect a q with 0 £ q £ p
per to > 0
has 
being Cr' the arc of circumference of the
advanced semiplan with |z| = R.
is had from which placing |f(x)| < mR x = Kingi j
e dx = i Kingi j dj ha
and taking advantage of that in [ 0,p/2 ] senj > 2j/p it is had : 
and therefore the lemma is demonstrated.
9) If f(x) it is a function defined on all the real axis
and can semislowly be extended analytically to the advanced semiplan
and in such it satisfies the Lemma di Jordan and it does not have
singular points on real axis $ 
being zk the singular points of the function f(z) in the
advanced semiplan.
10)Derivata logaritmica :
If f(z) it is a function analytics univoca with an ended
number of singolarità points isolates to you, all poles nobody of
which finds on the frontier of the dominion then the function 
member of the women's army auxiliary corps is said
derived logaritmica
11) Residual logaritmico :
Draft of residual of the function the member of the women's army auxiliary corps j(z) is estimated to you in its heads of singolarità.
12) Value of residual logaritmico in one zero of order k of the function f(z) :
The residual logaritmico is equal to the order of the zero.
It is demonstrated observing that if to is a zero of order n for f(z) then in its around can itself be written f(z) = (z-a)n f1(z)
this last one comes used in the calculation of
the function 
member of the women's army
auxiliary corps becoming simpler and remembering that the residual one
is equal to the coefficient of (z-a)-1 obtains that it is worth n that is is equal to the variety
of the zero.
13) Value of the residual logaritmico in a pole of order k of the function f(z) :
The residual logaritmico is equal to the order of the pole taken with the sign negative.
It is demonstrated observing that if to is a pole of order n for f(z) then in its around can itself be written f(z) = (z-a)- p f1(z)
this last one comes used in the calculation of
the functio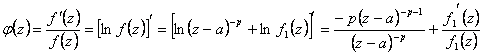n 
member of the women's army
auxiliary corps becoming simpler and remembering that the residual one
is equal to the coefficient of (z-a)-1 obtains that it is worth - p that is he is equal to the
variety of the changed pole of sign.
14) Theorem of the argument :
If f(z) it is a function analytics ovunque in a closed
dominion G except that in an ended number of singular points zk it situates you to the inside of
G. Supponiamo that all the zk are of the poles and that the function f(z) not
cancellations in no point of the G frontier of the dominion G
the difference between the number total of the zeroes N and the
number total of the P poles of the function f(z) of the G dominion is
defined from the expression 
.
The theorem is demonstrated calculating the integral to according to member through the theorem of the residual ones and observing that the residual logarithm of a function in a zero is just equal to the variety of the 0 and analogous the residual logaritmico in a pole he is just equal to the algebrica variety of the same pole.
15) geometric Interpretation of the theorem of the argument :
It must be replaced to the inside of the integral of the
theorem of the argument 
and to decompose the logarithm
like logarithm of the module more the times the variation of the
argument of the function, has 
In fact 
is a real
function univoca therefore the variation of its argument is 0 while 2°
the member expresses the variation of the argument that is the number
of turns totals around the point w=0 that the point w completes when
the point z covers the edge of the dominion in the positive sense.
16) Index of a point respect to one curve :
The index of a point respect to a curve sluice is the number of times that this comes covered regarding the point.
17) Theorem of Rouche :
If the functions f(z) and j(z) are analytics in the closed dominion G, and on the G frontier of the G dominion it is worth the inequality |f(z)|G > |j(z)|G the number total of zeroes of the function F(z) = f(z) j(z) is equal to the number total of zeroes of the function f(z).
It is had that the number of zeroes of the F(z) function is 
while for the function f(z) the number of zeroes
is 
embezzling member to member must find that
the difference between the number of the zeroes must be null.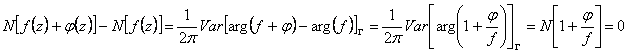 
is had in fact point w = 0 is found externally to
the circuit covered from w.
18) fundamental Theorem of algebra :
A polynomial of degree n it possesses in the complex plan n exactly zeroes (counting also their variety).
Us filler in condition of being able to apply to the
theorem of Rouche Hats to such aim if 
e 
is taken, writing the
relationship of the modules ha 
, is observed
that a circumference of such R beam can be always found that 
and therefore is had |g(z)| < |f(z)| therefore for the theorem of Rouche polynomial f(z)
g(z) possesses the same number of zeroes of the polynomial f(z) which it
has n zeroes all in the origin.