Range, Beta, functions of Bessel
Functions of Euler
1) Range di Euler:
draft of one olomorfa function in flat Rez > 0.
2) Formula of recurrence:
It is obtained calculating the integral for parts, is
had 
.
3) Formula of the factorial one:
It is obtained from the formula of recurrence 
; 
until
arriving alla 
and placing in it z = 1
the result is obtained.
4) Extension of the G(z) also to values denied you of z:
In gaining the iterando the formula
of recurrence until reaching the G(z n) is obtained to according to member an expression
multiplied for the G(z) that
therefore can be estrinsecata, obtains an independent relation from n
as it can be verified replacing n = n p, the relation has validity for
Re(z n) > 0 and introduces n singolarità polar.
5) Which relation alloy the G to the integral of Gauss :
It is obtained before replacing t=s2 in the definition of the G(z) and after ½ is placed z
= and it is remembered to us of the value of the integral of Gauss 
.
6) Beta of Eulero:
7) Relation between the Beta and the Range di Euler :
One replaces t=u2 in the G(p) and t=s2 in the G(q) dopodichè are multiplied between of they
collecting the common factors, are obtained 
replacing in which u=rcosq e s=rsenq
with duds=rdrdq is reached the
integral 
where 2 multiplied for the
integral are just the b(p,q)
that it can be obtained replacing t=cos2q .
8) Formula of the complements :
It is obtained writing the b in terms of the G therefore carrying out the 
substitution and resolving the integral that becomes the
indefinite integral of one function polidroma by means of the theorem
of the residual ones.
Functions of Bessel
9) Function generatrix of the functions of Bessel:
It is a olomorfa function to which a series of Laurent
with infinites is associated finishes to exponent negative and
infinites you finish to positive exponent, is had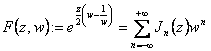 
that is where the J coefficientsn of this development are said functions of Bessel first
species.
10) Value of the coefficients Jn(z):
They are obtained to leave from the function generatrix 
I can multiply in how much the two series
converge absolutely is had 
and placing n-m=k it is
had 
therefore is had 
.
11) Demonstrate formula the J- n (z) = (-1)n Jn(z):
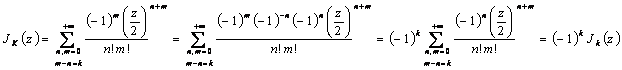is had.
12) Equation differentiates them of Bessel of order n:
It is an equation differentiates them in the 
shape its solution is the function of Bessel of 1ª species of order n. It is obtained deriving
both the members of the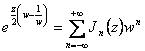 
regarding z and
regarding w, 
is had: from
which observing that multiplying or dividend for w it is gone to
modify its coefficient k, it is had:
and therefore
it is obtained
Jn - 1 - Jn 1 = 2 J'n.
Deriving regarding w instead has 
from which 
and therefore it is obtained 
.
Adding the 2 obtained relations 
is had and increasing it it is had 
, instead embezzling the 2 relations 
is had and deriving it regarding z 
is had and replacing last the 2 in the antepenultimate
one the equation is obtained differentiates them of Bessel 
.
13) Development of the trigonometrical functions in series of functions of Bessel:
It is obtained placing in the function generatrix w = andqthe obtaining therefore 
Estrinsecando is had 
From which equaling the real terms and the imaginary terms and placing j = p/2 the 2 following developments are obtained:
14) Application of the equation differentiates them of Bessel:
One its application is in the equation of the motion of one circular membrane.
15) integral Representation of the functions of Bessel :
Considering of being able to associate to the function a series of Laurent, i coefficients cn are estimated as an example with the curvilinear, typical integral of the residual one, calculating this integral obtain following :
One obtains remembering that the Jn(z) is not other that the coefficients of a series
of laurent and these are given from the integral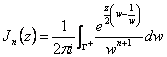 
and replacing w=ethe q the result is obtained.