Variable magnetic electric fields and in the time

1) Equations of Maxwell in the stationary case in the empty one :

 

2) Law of Faraday Neumann:

It means to describe phenomena in which a variation in the time of the flow of B concatenato with the circuit it induces in it a f.e.m. given from the flow variations can derive from one of the following causes :

to)    mechanical movement of the circuit

b)    variation of the B field in the time

c)    variation of geometry of the circuit

 

3) Electric field in not stationary conditions :

In not stationary conditions the electric field is not conservativo, is not worth more the that is but a dependency from the temporal variation of the B field is found, therefore like intuisce from the law of Faraday Neumann.

 

4) Law of Lenz :

F.e.m. that variation is induced in a circuit to continuation della del the flow of concatenato B is such from opporsi to this variation of flow, that is one will slide nel circuit induced current which it gives place to a B field that opposes to that it has generated it.

 

5) cut Flow :

In the case in which B it is constant and the circuit it is in motion, the cut flow is the flow through the walls of the cylinder that joins the circuit to the time t with the circuit to the time t'. It is equal to the variation of flow of the circuit.

 

6) Cause of the f.e.m. induced in the case of circuit in motion and firm source :

The force of Lorentz.

 

7) Cause of the f.e.m. induced in the case of firm circuit and source in motion :

It is always the force of Lorentz, enough to in motion choose a system of reference in which the source is firm.

 

8) Third equation of Maxwell in the not stationary case :

It is obtained from the being on this applies the theorem of the rotor and finally the integrandi are equaled to the 2 members.

 

9) f.e.m. autoindotta :

A circuit covered from variable current in the time gives to place to variable a B field also it in the time, a variation of the flow of B concatenato with the same circuit and therefore for the indurrà a f.e.m. will be had therefore that it is opposed to that one that has generated it.

 

10) Coefficient of self-induction :

Also inductance is said and turns out to be a coefficient of proportionality between the flow of B through the circuit and the current that it has generated B, in formulas has , measure in Henry and is only depended on geometric characteristics.

 

11) Coefficient of self-induction of a solenoid :

 

12) Coefficient of bifilar self-induction of one line :

being D the distance between the conductors and to the beam of everyone of they

 

13) Coefficient of self-induction of a coaxial cable :

 

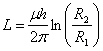
14) Constant of time of circuit LR :

 

15) Extracorrente of opening :

When a circuit is opened in which an inductance is present, the variation of the current and therefore of the flow is instantaneous and therefore for the law of Faraday Neumann elevating will be produced f.e.m. autoindotta much that spark to the heads of the switch can also succeed in to make scoccare one.

 

16) Law of Happy :

It establishes loads Q that flows in a circuit as consequence of a variation of the flow of B is had  .

 

17) Coefficient of mutual induction :

When 2 are had circuits covered from variable current in the time, well the current that slides in one of the 2 produces a B field that place to one f.e.m. induced concatena with the other circuit giving and therefore to one current. In formulas moreover is had

 

18) Energy possessed from one inductance covered from current :

represents the energy possessed from one inductance covered from current I

It is obtained multiplying for Idt the equation differentiates them of a circuit RL with generator characterizing the Lydian density of energy and integrating it between 0 and I.

 

19) Density of energy in a magnetic field :

It represents the present density of energy in a space region in which a field of magnetic induction of B. module is present Integrating it on a volume obtains is therefore many profits in order to calculate inductances laddove the method of the flows is of difficult application.

 

20) parasitic Currents or of Foucault :

If in a conductor a B field is had variable in the time, executing the circuitazione of and along a whichever closed circuit being finds a not null value therefore to the inside of the conductor circulates currents induced parasitic or of Foucault who embezzles energy to the magnetic field.

 

21) Density of movement current:

The movement current comes introduced in order to explain because if it is applied the theorem of the circuitazione with a surface that passes within the condenser obtains a various result regarding what it would be had with a surface that crosses a thread of the circuit that door to the condenser.

 

22) Current of movement :

Any S surface of the current of movement is the flow through one.

 

23) Quarter equation of Maxwell in the not stationary case :

It establishes the dependency of the rotor of B also from the temporal variation of the electric field.

It is obtained replacing la in the equation of continuità

 

24) Equations of Maxwell in the empty one in the not stationary case :

 

25) Equations of Maxwell in the matter in the not stationary case :