Theorems on the successions and the series of functions

Successions of functions

1) Criterion of punctual Convergence :

Necessary and sufficient condition because the succession of funzioni f_n converges punctually in To is that, fixed and > 0, " t?To N(and,t) such exists that : |f_n(t) - f_m(t)| < and " n, m > N .

 

2) Criterion of uniform Convergence :

Necessary and sufficient condition because the succession of funzioni f_n converges uniform in To is that, fixed and > 0, exists N(and) such that : |f_n(t) - f_m(t)| < and " t?A " n, m > N .

 

3) the limit of a succession of limited functions f_n convergent uniform is one limited function:

Part from the definition of the uniform convergence |f_n(t) - f_m(t)| < and if n, m > N after which it is sent n to ¥ and places m = N. To this point can use the triangular inequality and write |f(t)| - |f_N(t)| < |f(t) - f_N(t)| < and

ž placing and = 1 ha |f(t)| < 1 |f_N(t)| and therefore the sup of |f| it is limited from the sup of |f_N|

 

4) Theorem of the exchange of the limits

It is uniform in A e ž

I demonstrate before that the succession l_n to right of the equal one is convergent, we will find that its limit is l and the same limit will be had also for 1° the member. The convergence is settled down based on the criterion of uniform convergence, in fact it is had

|l_n - l_m| = |l_n - f_n(t) f_n(t) - f_m(t) f_m(t) - l_m| £ |l_n - f_n(t)| |f_n(t) - f_m(t)| |f_m(t) - l_m| < and being the smaller external module and modules and for centers them smaller of and for the convergence uniform in A. Rimane therefore solo to demonstrate that 1° the member in order to make that that is sets up the customary inequality of the limits |f(t) - l| £ |f(t) - f_N(t)| |f_N(t) - l_N(t)| |l_N(t) - l| £ 2and |f_N(t) - l_N| < 3and , where for the exteriors the uniform convergence of the l has been taken advantage of_n and for the term it centers them 2ª the hypothesis of the theorem.

 

 

5) If the succession of continuous functions f_n converges uniform ž its limit f is a continuous function.

It is demonstrated applying the theorem of the exchange of the limits to the function .

 

 

6) Theorem of the exchange of the limit with the derivative :

One is had succession of functions f_n : To® " derivabili and

to)    the succession of the derivatives {f_n^'} it converges uniform in (a,b) with limit g

b)    the succession of the functions {f_n} at least converges in a point t₀ ? (a,b)

ž also the succession f_n converges uniform in (a,b) and it is had

to) it must be demonstrated that {f_n} it converges uniform, that is is respected the necessary and sufficient condition of convergence |f_n(t) - f_m(t)| < and to such aim the theorem of Lagrange is applied from which taking advantage of the punctual convergence in t₀ and the uniform convergence of the succession of the derivatives {f_n^'} si it establishes the uniform convergence to f(t) of the succession {f_n }.

b) We suppose that {f_n(t)} it converges uniform to f(t) monster that f is derivabile, is had : from which being the relationship they increases derivabile as she is obtained still applying to Lagrange and the uniform convergence of the series of the derivatives, the two limits obtaining can be exchanged from which the thesis.

 

 

7)    Theorem of the exchange of the limit with the integral :

One is had uniform successionf _n of integrabili limited functions on the interval [ a,b ], convergent with limit f

ž

in how much is had the succession f_n converges uniform to f. must be only demonstrated the integrabilità of f which makes in terms of subdivisions taking advantage of the uniform convergence of f_n to f.

Series of functions

8) Criterion of punctual Convergence of Cauchy :

Necessary and sufficient condition because the series of functions Sx_n(t) converges punctually in To is that, fixed and > 0,

" t?To N(and,t) such exists that : |x_p(t) x_{p 1}(t) ... x_{p q}(t)| < and if n, m > N .

 

 

9) Criterion of uniform Convergence :

Necessary and sufficient condition because the series of functions Sx_n(t) converges uniform in To is that, fixed and > 0, exists N(and) such that : |x_p(t) x_{p 1}(t) ... x_{p q}(t)| < and " t?A if n, m > N .

 

 

10) Criterion of Weierstrass :

Given to the succession of functions x_n and one convergent series of positive constants Sc_n and definitively it is had |x_n(t)| £ c_n

ž the series of functions Sx_n(t) converges uniform in To.

It is demonstrated in virtue of the triangular inequality and of the criterion of convergence of Cauchy from which it derives

|x_p(t) x_{p 1}(t) ... x_{p q}(t)| < |x_p(t)| |x_{p 1}(t)| ... |x_{p q}(t)| < c_p c_{p 1} ... c_{p q} < and

 

 

11) Theorem of the convergence total :

If {x_n} normato and complete) the whose series of the S norms is one succession to values in a space of Banach (||x_n || it is convergent ž converges also the series Sx_n.

The demonstration already traces gained how much for the absolute convergence of the numerical series, analogous taking advantage of the Criterion of punctual convergence of Cauchy and the triangular inequality. The theorem is said of the convergence total in how much a series for which the series of the norms converges is said totally convergent.

 

 

12) Theorem of the limit of one series :

If Sf_n(t) is a uniform convergent series of functions with F(t) sum and exists the limit

ž the S seriesl_n converges and ha

 

13) the sum of a uniform convergent series of continuous functions is a continuous function.

The continuity of the sum of the series must be demonstrated that we remember to be equal to the sum of the rest n-esimo and the partial sum n-esima, considering the increment h has the two following equalities :

e embezzling member to member is obtained :

Where for 1ª the quadrant sum of continuousfunctionsis taken advantage of that S _n (x) is and therefore it continues while for 2ª and 3ª the quadrant the rest is taken advantage of that the series is uniform convergent therefore n-esimo can be rendered small how much vuo.

 

14) Theorem of the integral of one series:

A succession f _n ofintegrabili limited functions is had on the interval [ a,b ], if the series Sf_n(t) converges uniform in (a,b) with sum F(t) ž F is integrable and   is had

It is remembered that the sum of a S series is equal to the partial sum n-esima S_n(x) more the rest n-esimo R_n(x), integrating and passing to the modules it is had :

where the uniform convergence of the series has been taken advantage of. Therefore the theorem is demonstrated.

 

 

15) Theorem of the derivative of one series:

One is had succession f_n of derivabili functions and

to)    the series of the S derivativesf_n^' it converges uniform in (a,b) with G(t) sum

b)    the series of funzioni the Sf_n at least converges in a point t₀ ? (a,b)

ž   also the S seriesf_n converges uniform in (a,b) and it is had

S f _n'is g(x) = being uniform convergent for the previous theorem can be integrated term a.termine

where in the last passage the convergence to its sum of the series of functions has been taken advantage of. Deriving the previous expression S' (x) and therefore in definitiva S' (x) = S f _n 'is obtained g(x) =.

Series of powers

16) If a series of powers uniform converges in a point z₀ ? C

ž converges absolutely in every such point that |z| < |z₀| 

It is obtained for comparison with the geometric series in fact has 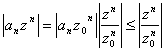where the convergence in point z ₀ formaggiorare with 1 has been taken advantage of the term. The last series is geometric and converges > |z| < |z₀| in the which case the relationship is smaller of then for the theorem of the comparison also is absolutely convergent.

 

 

17) Criterion of the root in order to determine the convergence beam :

Given the series the convergence  beam is ž r = 1/l è:

 

 

18) Criterion of the relationship in order to determine the convergence beam :

Given the series if the convergence beam exists 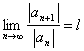 limite the ž r = 1/l è:

 

 

19) Property of the sum of one series of powers :

to)    the series it converges uniform in every circle : |z| £ r' with r' < r

b)    the sum of the series is a continuous function in |z| < r

c)    the series of the derivatives is still a series of powers that has the same beam of convergence

d)    the sum of the series is derivabile in complex sense with continuous derivative in |z| < r ; its derivative is equal to the sum of the series of the derivatives

a) demonstrates by means of the theorem of Weierstrass in fact the series converges absolutely for z = r' being inner it to the convergence beam and situated on the real axis therefore we have found a series of positive constants Sto_nr' that it converges and that maggiora our S seriesto_nzⁿ that therefore converges absolutely.

b)    Remembering that the sum f(z) of a uniform convergent series of continuous functions is continuous and date the uniform convergence of Sto_nzⁿ as soon as demonstrated and the arbitrariness of the point r', the theorem turns out demonstrated.

c)    is had that it is a series of powers with coefficients b_n = (n 1)a_{n 1} , applying the criterion of the root is obtained and therefore the convergence beam is the same one of to_n .

d)    sufficient E' to write f_x and f_y and to verify that they satisfy the relations of Cauchy - Riemann.

 

 

20) Other property of the sum of one series of powers :

to)    the sum of the series of powers it is of class C^¥ in |z| < r

b)    the derivative k-esima of the sum of the series is equal to the sum of the series of the derivatives k-esime.

c)    Between the coefficients of the series and the sussiste derivatives of the sum f(z) the relation

a) Segue from the fact that the series of the derivatives is still one series of powers with the same beam of convergence.

b)    E' exactly the point d) of theorem 19)

c)    is obtained in practical way deriving the sum of the series

 

 

21) Theorem of Abel :

If a series of S powersto_nzⁿ converges in one of the extreme points of its convergence interval

ž the convergence interval includes also this point.

The uniform convergence is had if is demonstrated that the rest n-esimo is smaller ofand

being can be written from which collecting xⁿ is had can therefore be taken advantage of the uniform convergence that renders all the rests n-esimi smaller of and / 2 collecting which remain within parenthesis the development of the geometric series for which the sum is becoming simpler is obtained that the rest n-esimo is smaller of and .

22) necessary Condition for the sviluppabilità in series of Taylor of one function f:

It is f ? C^¥ (- r, r) and one constant M, independent exists from n and from x such that is had, definitively ž f is sviluppabile in series of taylor in (- r, r).

The condition in the rest n-esimo obtaining is replaced that it stretches to 0 for n that stretches to ¥.