Theorems on multiple integration
1) To with it is limited
To its frontier is measurable > is measurable and has measure 0
2) If I have a continuous function on compact a measurable T
its diagram is with limited and measurable and has null measure.
The function is continuous on a compact one therefore for Heine - Cantor is also uniform continuous that it implies that if I take w' and w' ' ? T such che || w' - w' ' || < d then is had che || f(w') - f(w' ') || < and.
A regular decomposition (of diametro is carried out < d) of a rectangle which it contains the T dominion.
For Bolzano Weierstrass (If and "n it is a closed entirety and limited Max(E) and Min(E) exist)
on everyone of the T the will exist the maximum and the minimum of the
function, and an interval of is created "with 3
height comprised between the minimum and the maximum assumed
from the function on spaces out. Therefore the measure of the
surface is given from the sum of the measures of these 3
intervals of " that is 
< and in how much the
function is continuous on a compact one therefore for Heine - Cantor
is also uniform continuous that it implies that if I take w' and w' ' ? T such that || w' - w' ' || < d
then is had che || f(w') - f(w' ') || < and.
3) the cilindroide is with measurable:
Enough to demonstrate that a its frontier has null three-dimensional measure therefore it is in fact up for the f(x, y) for the previous theorem and therefore is for the base in how much has height 0 like pure for the sidewall, both in fact can be enclosed in a plurirettangolo of "3 of infinitesimal measure.
4) If I have one constant function compact L on a measurable one of T base? "2 and therefore D is the cilindroide of T base, is had :
It is supposed that the base is contained in plurintervallo P2 and contains plurintervallo the Pthat is 1 P1 ? T ? P2 therefore has m(P1) < m(T) < m(P2), of the L rest is constant therefore Lm(P1) < Lm(T) < Lm(P2) with Lm(T) = m(D) is had therefore
|m(D) - Lm(t)| < L |m(P2) - m(P1)| £ L and in how much for the theorem of Heine Cantor if f it is continuous on a compact one then f are uniform continuous and therefore if the distance between the two points of the dominion is < d the distance between the images he is smaller of and .
5) If I have a continuous function on compact a measurable T? "2 and therefore D is the cilindroide of T base, is had :
For the theorem of Heine Cantor being the continuous function on a compact one is also uniform continuous therefore choosing a smaller amplitude of d for the regular decomposition of the T dominion will obtain one distance between the images smaller of and .
to) sTo,p = 
is comprised between the sum of Cauchy that uses the
minimum of the function on every floor tile of the regular
decomposition and the measure of Cauchy that instead employs the
maximum.
b) the measure of the cilindroide S m(Di) is comprised between the measure of the cilindroide that uses the maximum value of the f on every floor tile and the measure of the cilindroide that uses the minimal value of the f on every floor tile.
They give a) and b) dato that the difference between
maximum and minimum is on every smaller floor tile of and then is had che | sTo,p - l | < and in fact 
6) Formula of reduction for double integrals:
If f it is continuous on simple a T dominion regarding
axis x 
Single geometric interpretation
7) Formula of reduction for triple integrals by means of integration for threads:
If f it is continuous on simple a T dominion regarding the
plan xy 
Single geometric interpretation
8) Formula of reduction for triple integrals by means of integration for sections:
If it is had to < x < b and the sections of D with an orthogonal plan to axis x are measurable then are had :
Single geometric interpretation
9) Formula for the change of variable:
If To he is compact a measurable one having like T image and r(u, v) it is a biiezione whose jacobiano is not null
Single geometric interpretation
10) Theorem Guldino Bread:
The volume of the solid S that is obtained from a complete
spin around to the axis z of contained limited and measurable a T
entirety in plan x = 0 is given from the formula 
being 
the coordinate of the
centroide.
It is obtained passing in polar coordinates and
remembering the definition of baricentro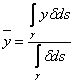 
.