Theorems on the implicit functions
1) Theorem of Dynes :
It is g : To® " , To opened of "2 . We suppose that :
to) g e gy they are continuous in To.
b) in point x0 , y0 ? To one has g(x0 , y0) = 0 and gy (x0 , y0) ¹ 0.
a 0 around exist U ofx and an only function f : U® " , continues in U, such that y0 = f(x0) and that g(x, f(x)) = 0 for every x ? U.
If moreover gx are
continuous in To f he is
derivabile in U and it is worth the formula 
" x ? U.
The scope is that one to bring back itself to being able
to apply the theorem of the zeroes on an opportune interval (If a defined continuous function on an interval [ a,b ]
assumes to its extreme not null values and of opposite sign, then f
admits at least one zero y ? (a,b)) For the location of the
interval applies the theorem of the permanence of the sign to the gy that we would suppose
positive gy (x0 , y0) > 0 (if 
then f(x) > 0 definitively for x ® x0 where the
term definitively indicates that the property is valid for every x
pertaining at least one around of x0 with x ¹ x0 .)
therefore the function of single y g(xthe 0 ,y) is closely increasing and since g(x0 , y0) = 0 necessarily will be
g(x0 , y0 - b) < 0 e g(x0 , y0 b) > 0, moreover analogous relations are not only worth in x0 but also in one wrap
[ x0 - d , x0 d]. To this point choosing xa pertaining to this wraps for the theorem of the zeroes will have to exist a y such that g(x , y) = 0 replacing and = b obtain that f it is continuous in you wrap [ x0 - d , x0 d].
In order to demonstrate the formula the theorem of the
valor is used medium (If f it is continuous in [
a,b ] and derivabile in (to, b) exists one such point c that 
) is
had therefore g(x, y) - g(x,y) = 0 = gx(x,h)(x-x) gy(x,h)(y-y)
from which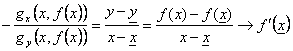 
is obtained.
2) Theorem of Dynes in more than 2 variable ones:
It is g : To® " , To opened of "n 1 . We suppose that :
to) g e gy they are continuous in To.
b) in point x0 , y0 ? To x are hadg(0 , y0) = 0 and gy (x0 , y0) ¹ 0.
a 0 around exist U ofx and an only function f : U® " , continues in U, such that y0 = f(x0) and that g(x , f(x)) = 0 per every x ? U.
If moreover gx1 ,.., gxn is
continuous in To f is
derivabile in U and it is worth the formula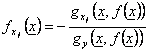 
" x ? U
Analogous demonstration to that it is had in the three-dimensional case.
3) Theorem of Dynes for systems:
It is g : To® "m , To opened of "m n . We suppose that :
to) g he is derivabile in To.
b) in point (x0 , y0) ? To x are hadg(0 , y0) = 0 and det Dyg (x0 , y0) ¹ 0.
exist one around V of x0 and an only
such function y = f(x) that f is derivabile in V ed y0 =
f(x0)
and that g(x , f(x)) = 0 per every x ? V.
Moreover is worth the formula 
.
Being :
4) Theorem of Lagrange:
They are f,g derivabili in an open X of "2 and is (x0 , y0) a regular point for and0 = {(x,y) ? "2 : g(x, y)=0}
(x0 , y0) are a bound critical 0 and point > $ such a real number l that `f(x0 , y0) = l `g(x0 , y0)
Be a matter of a bound critical point (a regular point for which the derivative of f in tangent direction to the tie) the gradient of f is cancelled it will have to be normal to the tangent therefore as of the rest gradient of g must happen for the carrier.
? From the equation it follows that the gradient of f is normal to together and0 in point (x0 , y0) and therefore the point is critical bound.
5) Method of the multipliers of Lagrange:
to) it is necessary to characterize the singular points of the tie. Enough to set up the determining Jacobiano and to impose that it is null.
b) the free ends of the lagrangiana are characterized.
c) the nature of the estremanti points is obtained from the study of the derivatives of the implicit function which are gained or through the theorem of Dynes or the symbolic derivative of composed function.