Theorems on the Equations differentiate them ordinary
Equations differentiate them of 1° degree
1) Theorem of the contractions of Banach - Caccioppoli :
In a complete metric space a contraction admits always an only fixed point.
Existence :
taken one point x0 arbitrary we will construct one succession that converges to one point x~ : F(x~) = x~ La succession is defined ricorsivamente like xn 1 = F(xn). Taking advantage of the fact that F is contraction it succeeds to establish that
d(xn 1 , xn) £ rn d(x1 , x0) turned out that it comes used in order to
demonstrate that the succession is fundamental in how much of given
Cauchy that d(xn , xm) £ and . It is had in
fact : 
from which collecting and
replacing the sum of the harmonic series 
is
obtained that it stretches to 0 for m® ¥ being 0 < r < 1, therefore the succession is of
Cauchy and therefore it converges.
Supponiamo that the limit ofthe argument converges then to x ~ taking advantage of the continuity of the F contraction pu² to become the limit of the function and therefore to demonstrate that to F(x~) = x~ .
Oneness :
We suppose that 2 fixed points, the distance between of they taking advantage of the contraction definition, cannot that exist be 0, therefore the 2 points in truth are the same point.
2) Condition of Lipschitzianità for f :
If f and its partial derivative respect to y is continuous in D f is locally lipschitziana respect to y, uniform in t.
It is demonstrated applying the theorem of the valor
medium 
3) If the succession of continuous functions fn converges uniform its limit f is a continuous function.
It is demonstrated applying the theorem of the exchange of
the limits to the function 
.
4) Lemma di Volterra:
If j ? C1(the d) is solution of the problem of
Cauchy j satisfies the equation integral of
Volterra 
" t ? Dthe and viceversa.
E' clearly that if j is solution of the problem of Cauchy it can integrate the first equation of the problem between t and t and replacing the condition begins them j(t) = x .
? It is obtained deriving in how much j it is continuous and it has derived continuous in virtue of the equality with 2° the member.
5) Theorem of existence and local oneness :
It is f : D® "n with open D of "n 1 , continues in locally lipschitziana D and in D, respect to y and uniform in t
for every point (t,x) ? D exists aroundthe d of t such thatthe d = [t-d , t d] in which one is defined solution of the problem of Cauchy. Such solution is only in the sense that every other solution coincides with j in the common interval of definition.
The demonstration is articulated in the three following steps :
to) the correspondent is associated
to the problem of Cauchy equation of Volterra
b) a complete metric space is characterized
A complete metric space is the space of the continuous functions on a compact one, therefore " (t, x) ? D characterizes a compact G : = {(t,y) ? "n 1 : ||t-t|| < a and ||y-x||< b}, to its inside we characterize the metric space Y of the continuous functions with diagram contained in G , Y : = { j ? C(Id) : ||j(t) -x||< b} it is a complete metric space to pact to adopt the metric one of the uniform convergence d(j, y) = max || j(t) -y(t) ||
c) is demonstrated that correspondent to the equation of Volterra works them is a contraction and therefore characterizes an only fixed point that is an only solution.
To the equation of Volterra it is associated works them 
, characterizing hour of the restrictions on d is in a position to making
to see that draft of one contraction :
to) We want that it is F[y ] ? Y
being
M : = max || f(t, y(t) || we must impose Md < b and therefore d < b/M.
b) We want that it is contraction
that is 
from which taking advantage of the
local lipschitzianità of f it is had : 
where the last inequality is motivated from the choice
of the metric one of the uniform convergence. Therefore
contraction on condition that L is oned < 1 > d < 1/L.
Choosing d = min (to, 1/L, b/M) the theorem is demonstrated.
6) Condition for the existence of one skillful massimale solution :
It is f : D® "n with open D of "n 1 , continues in locally lipschitziana D and in D, respect to y and uniform in t
is y :[t0 , b) ® "n one limited skillful massimale solution b = b
To demonstrate.
7) Lemma di Gronwall :
They are The ? " an interval and t ? They are moreover u,v :The ® " two continuous in I, not negative functions and c and " .
If 
" t ? I
" t?I.
supposing t > t is and multiplying per 
in how much is had the function to
first member is decreasing having negative derived it in
fact : 
in how much has v(t) £ w(t) and quindi w' (t) =
u(t)v(t) £ u(t)w(t)
Therefore 
therefore 
..
8) Theorem of existence and total oneness :
It is S : = (t1, t2) x "n Supponiamo that f it is defined in S and that in S f is continuous and locally lipschitziana respect to y and uniform in t. If moreover 2 such positive B exist and constants To that ||f(t, y)|| £ To B||y|| " (t,y) ? S
" (t,x) ? S, j(t ;t,x) are defined in t1 , t2 .
For the previous theorem enough to demonstrate
that the y(t) it is limited so that the interval to us he is
massimale, to such aim normando the integral equation of Volterra 
is had :
Therefore y(t) it is limited and therefore it admits
massimale solution.
9) Theorem of existence and total oneness :
It is f : (t1, t2) x "n ®" a continuous and totally lipschitziana function in Y with L constant
" (t,x) ? S, j(t ;t,x) are defined in t1 , t2 .
To demonstrate.
10) Theorem of the dependency of the solutions from the data begins them :
It is f :D® "n continues and locally lipschitziana respect to y, uniform in t. Supponiamo moreover that in around of point (t0, x0) are stung in which every solution it is defined in a common interval to tutte moreover if (t ,x) ®(t0 ,x0 ) j(t ;t,x)®j(t ; t0 , x0)
Methods of resolution of equations differentiate them of 1° the order
11) resolutive Formula of the equations differentiates them linear :
They are equations in the shape 
, the general integral is given from the formula :
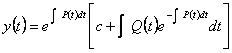
12) resolutive Formula of the equations differentiates them exact :
They are equations in the shape 
, the general integral is given from the formula :
being F(t, y) a function upgrades them
13) Equations to variable separabili :
They are equations in the shape 
, the general integral is given from the formula :
14) Equations of Bernoulli :
They are equations in the shape 
, they resolve dividend for yto and resolving the turning out equation it
differentiates to delineate them of 1° the order.
15) homogenous Equations or of Manfredi :
They are equations in the shape 
, they resolve ponendo 
and resolving the
turning out equation it differentiates them to variable separabili.
16) Like resolving equations of the type y = F(x, y') :
It must be placed y' = p therefore to derive respect to x, replacing therefore p' = dp/dx an equation to variable separabili is obtained resolving which gain x and y according to p
17) Equations of Of Alembert - Lagrange :
Draft of equations in shape y = x g(y') f(y'), is resolved placing y' = p therefore to derive respect to x, filler therefore to a linear equation in function of the x resolving itself which obtains one parametric solution of x and y according to c.
Equations differentiate them of order n
18) Criterion base for the trattazione :
Every equation differentiates them of order n can be led back to a linear system of n equations of 1° the order therefore in order to demonstrate the existence and the oneness of the solution, can be made resorted to how much already demonstrated per le equations differentiates them of 1° the valid order and also for the linear systems to pact to change the simbolismo.
19) necessary and sufficient Condition because n solutions of the equation are linearly independent :
The determining one of the wronskiana matrix must be 0
¹ 0
20) Theorem of Liouville :
The wronskiano of an equation differentiates them of order
n satisfies la 
To demonstrate
21) Theorem of Lagrange:
They are y1 ..., yn n independent solutions of the homogenous one, a solution of not - homogenous it is supplied from the formula
22) Theorem of superimposition:
If b(t) = b1(t) b2(t) and we know a particular integral of the equation with famous term b1(t) and one of the equation with famous term b2(t) the sum of the 2 integrals sarè an integral of the equation with famous term b(t)
Systems of equations differentiate them of 1° the order
23) Criterion base for the trattazione :
The criteria of existence and local and total oneness are same ad.eccezione.della the notation.
24) necessary and sufficient Condition because n solutions of the equation are linearly independent :
The determining one of the wronskiana matrix does not have
to be null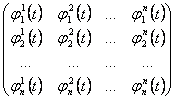 
25) Theorem of Liouville :
The wronskiano of a system of solutions of the equation 
satisfies the equation differentiates them 
where a(t) it is the trace of the A(t) matrix.
26) Corollario of the theorem of Liouville :
The wronskiano of an equation differentiates them of order
n satisfies la 
where a(t) it is the trace
of the representative matrix
27) Method of variation of the arbitrary constants (Theorem of Lagrange):
In order to obtain the general solution of the not
homogenous system 
ricavabile particular solution
through the formula:
is sufficient to add to the general solution of the
correspondent arranges homogenous one as an example 
