Site Visited 498534 times Page Visited 68 times You are in : Etantonio/EN/Universita/2anno/Analisi2/     

Definitions of Analysis 2

Series

1) Series:

Draft of a succession {sn}nella which the order element n is equal to the sum of the first n terms of one succession {ton}. As an example 3° the element of the series is the sum of the first 3 terms of the succession {ton}, to0 to1 to2 .

 

2) Sum partial n-esima or reduced n-esima sn :

Draft of the single element of the succession {sn } that is of the sum of the first n terms of the succession {ton }.

 

3) Series of terms ton:

= to 0 to 1 to 2 ...... to n is indicated.

 

4) Sum of the series:

Draft of the value of the term n-esimo of the succession {sn} for n® ¥ in the case that such value is ended that is in the case that the series converges.

 

5) Rest of the serie:

The rest n-esimo of the series is and in the case that the series converges to To, = R n = To - is had sn .

 

6) Character of the serie:

Draft of the characteristics of the sum of the terms for n® ¥ , it can be convergent, divergent or irregular.

 

7) geometric Series of reason q: converges to if |q| < 1.

 

8) Series of Mengoli : converge to

 

9) Series Telescopiche : converge a to0 -

 

10) Series Armonica : diverges

 

11) When the series ton is absolutely convergent?

it is absolutely convergent if the series set up with the module is convergent in the which case also converges while the contrary is not always true.

 

12) When the series is conditionedly convergent?

When it is convergent but is not convergent.

 

13) When the series is a riordinamento of the series ?

When biiettiva application j that b n = toj (n) exists one such.

 

Spaces work them

14) fundamental Succession or of Cauchy:

A succession {ton} to real values says fundamental or of Cauchy if "and> 0 exist a N?? such that |ton- tom| <and for every brace n, m > N.

15) complete metric Spazio:

It is a metric space in which every fundamental succession it is convergent.

 

16) Convergence puntuale :

One succession of functions fn : To® " it will be said convergent in To, with limit f: To® " if, fixed and > 0 " t?To, $

N = N(and,t) such that |fn(t) - f(t)| < and if n > N.

 

17) Convergence uniforme :

One succession of functions fn : To® " it will be said uniform convergent in To, with limit f: To® " if, fixed and > 0

$ N = N(and) such that |fn(t) - f(t)| < and if n > N.

18) Criterion of convergence of Cauchy or convergence puntuale :

Necessary and sufficient condition because the succession of functions fn : To® " it converges punctually in To is that fixed and > 0, " t?To, $ N = N(and,t) such that |fn(t) - fm(t)| < and " t?A se n, m > N.

 

19) Criterion of uniform convergence:

Necessary and sufficient condition because the succession of functions fn : To® " it converges uniform in To is that fixed and > 0 $ N = N(and) such that |fn(t) - fm(t)| < and " t?A se n, m > N.

 

20) Application Lipschitziana :

A metric space is (X,d), an application F:X®X says lipschitziana if a such number exists r > 0 that, " brace x,y of points of X is had d(F(x), F(y)) £ rd(x, y).

 

21) Spazio di Hilbert:

It is a metric space (on it is defined one distance) and suit.

 

22) orthogonal Functions:

2 functions say orthogonal if their product to climb is null.

Series of functions

23) Criterion of convergence of Cauchy or convergence puntuale :

The series of functions: To® " it converges punctually in To >fixed and > 0, " t?To an index N = N(can be determinedand,t): " p ³N and " q ³ 0 is had |xp(t) xp 1(t) .... xp q(t)| < and .

The convergence will be uniform > $ N = N(and) such that |xp(t) xp 1(t) .... xp q(t)| < and " t?A " p ³ N " q ³ 0.

 

24) Corollario of the criterion of Cauchy:

If converges punctually (uniform) in To ž ® 0 punctually (uniform) in To.

 

25) totally convergent Series:

It is a series for which the series of the norms converges.

Series of powers

26) Expression of the series of powers:

 

27) Circle and beam of convergence:

Given that the series converges in z0 ž it converges also in |z| < |z0| that it is a circle centered in the origin and of beam

r: = Sup{r: R < |z0|}, such circle and such beam are said of convergence.

 

28) advanced Limit or maximum limit:

It is the maximum of the values limit, is ¥ if the succession is not limited advancedly.

 

29) inferior Limit or minimal limit:

It is the minimum of the values limit, is ¥ if the succession is not limited inferiorly.

Series of Taylor

30) Series of Taylor:

 

31) Function analytics:

A function says analytics in point x0 ?To if he is sviluppabile in series of Taylor in one around of x0 .

Series of Fourier

32) trigonometrical Series:

Draft of the serie

 

33) Value of the coefficients of the series of Fourier :

 

34) continuous Function to tratti :

Draft of a continuous function on [ a,b ] except to more a n° ended than points in which exists ended the limits skillful and left and therefore discontinuity of 1ª species is one.

 

35) When f ? C2p :

f it is periodic with period 2p and is continuous at times.

 

36) Condition of Dirichlet:

A function satisfies in point x0 the condition D di Dirichlet if verification at least one of following :

to)    he is derivabile in x0

b)    and equipped ofskillful and left derivative in x is continuous in x 00

c)    has a discontinuity of 1ª species in x0 and exists ended the limits e

 

37) Typology of convergence to f of the series of Fourier :

to)    In average quadratic

b)    punctual Convergence

c)    uniform Convergence

 

38) Spazio di Hilbert :

X it is a linear space with product to scale < f,g > = and is complete regarding the induced norm.

Equations differentiate them

39) Equation differentiates them:

It is a function that implies one incognito function and its derivatives.

 

40) Order of one equation differenziale :

It is the order of the derivative of maximum order that appears in the equation.

 

41) Degree of one equation differenziale :

It is the exponent of the maximum power of the derivative of the maximum order that appears in the equation.

 

42) Equation differentiates them ordinary:

It is an equation in which the incognito function it depends on one single variable independent.

 

43) Equation differentiates them to the derivatives parziali :

It is an equation in which the incognito function it depends on one or more variable independent.

 

44) Equation differentiates them in shape normale :

It is an equation in which the derivative of the maximum order can be esplicitare.

 

45) Solution of an equation differentiates them:

A continuous function on®a D openis f:D "n of "n 1 , then one function y :The ® " of [I ] There such class that (t, y(t)) ? D and t? Solution of the equation is said differentiates them y' (t) = f(t, y(t)) on condition that it satisfies it identicamente

" t?Being a not degenerate interval.

 

46) general Solution of an equation differentiates them:

It is with of all the particular solutions of the equation differentiates them.

 

47) Problem of Cauchy:

It is a system constituted from an equation differentiates them and or more conditions it begins them that they assign to the incognito function a data value to the moment t. Once characterized the general integral can be determined the particular solution replacing the conditions begins them.

48) Lipschitziana Function:

The application f(t, y) is lipschitziana in D respect to y, uniform in t, if constant L exists one dictates constant of such Lipschitz that ||f(t, y)-f(t, z)|| £ L ||y-z|| for every brace of points (t,y) and (t,z). in D.

49) Function locally Lipschitziana:

F(t, y) is locally lipschitziana in D respect to y, uniform in t, if every point of D possesses around in which constant L exists one dictates constant of such Lipschitz that ||f(t, y)-f(t, z)|| £ L ||y-z|| for every brace of points (t,y), (t,z) pertaining to around. The difference regarding the previous one is therefore only that L can depend on around.

50) fundamental Succession or of Cauchy:

A succession is fundamental if " and > 0 a such N exists that 2 whichever greater elements n and m of N in the dominio taken of the succession have themselves that | ton - tom | < and

51) complete metric Spazio:

A metric space is deto complete if every succession in defined it converges to a point of the same space.

 

52) Contraction:

Lipschitziana application ove 0 < L < 1 is one.

 

53) fixed Point:

It is a point that comes transformed in if same from the application.

 

54) Spazio di Banach:

It is a normato and complete space (Every fundamental succession is convergent).

 

55) general Integral of one equation to climb of N order:

is considered where f : (to,b) x "n ®" is continuous and totally lipschitziana ž

Is said general integral of the problem of Cauchy correspondent one family of solutions y(t, c1...,cn) defined to varying of (t,c1...,cn) ? X J1 x.... x suchJ n that :

to)    " fixed (c1...,cn) ? J the function j(t) = y(t, c1...,cn) is solution of the problem of Cauchy

b)    " fixed (t0 , y0 ..., y0(n-1) ) ? The x "n exists (c1...,cn) ? Only J such that y(t, c1...,cn) satisfies the conditions begins them

 

56) general Integral of a linear system of equations differentiates them:

(t) is considered y' = f(t, y(t)) where f : X "n the ® "n is continuous and totally lipschitziana ž

General integral of y' (t) is said = f(t, y(t)) a carrier y(t, c) : (t,c) ? IxJ, J ? "n such that :

to)    " fixed c ? J the function j(t) = y(t, c) is solution

b)    " fixed (t0 , y0) ? The x "n exists c ? Such only J that j(t) = y(t, c) satisfies y(t0) = y0 .

 

57) linear System :

Draft of an equation vectorial of the type with A(t) dictates matrix of the coefficients and b(t) said famous term.

Quadriche

58) Write the generic equation of the ellissoide and to describe of varying:

ellissoide is called because if we cut it along axis z = 0, x = 0, y = the 0 sections are ellipses.

varying is:

to) if to according to member there is the -1 then ellissoide is imaginary

b) if the famous term is 0 the ellissoide is reduced to a point

 

59) Write the generic equation of the iperboloide to one stratum and to describe of varying:

iperboloide to a stratum is called because if we cut it along axis y = 0 and x = 0 the sections are hyperbolas while if we cut along plans parallels to it to the plan xy we obtain of the ellipses. It does not have varying.

 

60) Write the generic equation of the iperboloide to two stratums and to describe of varying:

iperboloide to two stratums is called because if we cut it along axis y = 0 and x = 0 the sections are hyperbolas while if we cut along plans parallels to it to the plan xy we only obtain of the ellipses for advanced values of |c|

it does not have varying.

 

61) Write the generic equation of the cone and to describe of varying:

This is a homogenous equation in how much appears all elements of the same degree wants to say that it can be constructed only using a bundle of straight. From a mathematical point of view it coincides with the norm.

varying is.

to) if the coefficient of z2 is positive then the cone is imaginary.

 

62) Write the equations of the paraboloidi and to describe of the characteristics:

is a elliptic paraboloide, is obvious that its sections are of the ellipses, is not that a convex goblet, for values of z smaller of 0 comes described a elliptic paraboloide imaginary .

is a hyperbolic paraboloide or saddleback, is obvious that its sections long plans parallels to the plan xy are of the hyperbolas while sezioni parallels to the plan yz are of the concave parabolas while the sections parallels to the plan zx are of the convex parabolas.

 

63) Write the equations of the cylinders and to describe of the characteristics:

is a elliptic cylinder

is an imaginary elliptic cylinder

is a hyperbolic cylinder

is a parabolic cylinder

 

64) For which reductions of quadriche they are obtained of the plans?

a) 2 autovalori and correspondents null linear terms

x2 = tn ž if tn > 0 2 real plans are had parallels

if tn = 0 2 real plans are had coinciding

if tn < 0 2 complex plans are had parallels

b) 1 autovalore 0 and others 2 of sign discorde, tn = 0

x2 - y2 = 0 ž 2 plans incidents

c) 1 autovalore the 0 and others 2 of Concorde sign, tn = 0

x2 y2 = 0 ž 2 complex plans incidents whose intersection is the real axis z.

Multiple integration

65) pluridimensionale Interval:

The 1 is the produttoria*the 2*the 3*... *nthe being a limited interval of ends tothe e bthe .

Its measure is

 

66) Plurintervallo :

Draft of the P union = being itself Qi an interval that does not have other points in common with others intervals.

The measure of the plurintervallo is equal to the sum of the measures of the Q intervals that they constitute it.

 

67) limited inner Measure of with To mthe (a):

Draft of contained the advanced end of the measure of the plurintervalli in To.

 

68) Measure esterna limited of with To m and(a):

Draft of the inferior end of the measure of the plurintervalli that they contain To.

 

69) Entirety misurabile :

An entirety is said measurable if the inner measure and the external measure are equal.

 

70) regular Decomposition:

A family of sets is said regular decomposition of the T entirety if :

to)    every T entiretythe is limited and measurable

b)    the union of sets the Tthe gives back the T entirety

 

71) Amplitude of one regular decomposition :

Draft of the maximum of the diameters of Ti .

 

72) Dominion :

It is the entirety given from the union of with with its frontier.

 

73) Cilindroide:

Is the solid one characterized from i points x, y, z such that x and y belong to the T dominion? "2 while the z it varies between 0 and f(x, y).

 

74) integrable Function second Cauchy :

A limited function says integrable according to Cauchy on compact a measurable T if being: d  exists finito is the amplitude of the regular decomposition

To regular decomposition of T is one

p is with of i points mi everyone of i which belongs to one various Ti .

sTo,p is the measure of equal Cauchy to the sum

The 0 limit is ended if " and > 0 exist d 0 > such that for every regular decomposition To of amplitude d(a) < d0 and for every entirety p of points is had that | sTo,p - l | < and .

 

75) simple Dominion regarding the axis x :

It is a such dominion that to < x < b while to(x) < y < b(x)

 

76) simple Dominion regarding the axis y :

It is a such dominion that c < y < d while to(y) < x < b(y)

 

77) simple Dominion regarding the plan xy :

It is an entirety constituted from points (x, y, z) such that x and y belong to the dominion while to(x,y) < z < b(x,y)

Implicit functions

78) Equation of the straight tangent to the diagram of the implicit function in point x0 , y0 :

 

79) With of livello :

It is the entirety that is obtained projecting on plan z = 0 the obtained entirety intersecting the diagram of z = g(x, y) with plan z = c

 

80) singular Point or critico :

Draft of a point in which the gradient of function `g(x0 , y0) = 0 is said singular im how much is not applicable the theorem of Dynes.

 

81) Characteristic of with of livello :

If with of level it is lacking in singular points, in every its point the tangent is orthogonal to the direction of maximum increase of g in that point that is `g.

 

82) Envelope of one family of curve :

Draft of one tangent curve, in every its not singular point, to one and one single curve of the family.

 

Bound ends

83) Jacobiano:

He is the determining one of the matrix superficial being j andy of "3 that characterizes one curve. It represents the rate relative variation of the area, subordinated to the change of variable.

84) regular Point:

Draft of a point in which the g(x, y) = 0 that defines a function implicitly tie affinche happens, for the theorem of Dynes must be `g(x0 , y0) ¹ 0. For De Blasi instead a point it is to regulate if the rank of the Jacobiano is 2.

 

85) bound critical or stationary Point:

Draft of a regular point for the tie in which the derivative of the objective function in tangent direction to the vincolo. is cancelled For De Blasi instead a point is to regulate if the rank of the Jacobiano is £ 1.

 

86) Lagrangiana :

It is the equazione f(x, y) - l g(x, y)

Vectorial analysis

87) Parametrizzazione of a sottoset of "3 :

Draft of a continuous function r :® "3 whose image is the sottoset of "3 also said support of the curve and coinciding with the trajectory.

 

88) simple Parametrizzazione:

A parametrizzazione is simple if the function r is iniettiva.

 

89) Curve:

Parametrizzazione coincides with the brace (support,).

 

90) flat Curve:

it is a curve whose support is contained in a plan.

 

91) Direction of one curva :

The direction is function of the parametrizzazione, which has like dominion " that it is oriented and therefore it will be also to curve.

 

92) regular Curve:

Is one having curve derivabile parametrizzazione and r' (t) ¹ 0 for every t ? I.

93) equivalent Curves:

Two curves are said equivalents if they can be obtained from the other with a change of parameter that not dumb the direction.

 

94) Curves omotope:

Two curves g1 and g2 are said omotope in and if a continuous function exists j = j(t,l), (t,l) ? [ to, b]x[0, 1 ] such that :

to)    j(t,0) = r1(t) ; j(t,1) = r2(t) " t ?[ a,b ]

b)    j(to,l) = pto ; j(b,l) = p(b) " t ?[ 0.1 ]

and finally " l ?[ 0.1 ], the equation curveg l j = j(t,l) is contained in and.

 

95) Length of one curve:

It is obtained applying the theorem of Pitagora to the infinitesimal increment in order to calculate then ds and adding the ds.

 

96) curvilinear Abscissa:

It is the distance covered calculated along the trajectory beginning from a point begins them, it is worth :

deriving one obtains that s' (t) > 0 in how much the norm is positive and therefore the parametrizzazione by means of curvilinear abscissa is positively equivalent.

 

97) curvilinear Integral of 1ª species:

To every infinitesimal element of the curve property is assigned one to scale, the curvilinear integral of 1ª species does not make other that to calculate the sum of these contributions long all the curve, in formulas :

in the case that f = the 1 integral gives back the length of the curve, therefore this integral is independent from the direction of the same curve.

 

98) Examples of I use of the curvilinear integral of 1ª species:

to)    calculation of the mass of filo a

b)    calculation of the barycentre of the thread stesso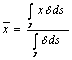

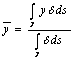
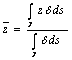
c)    calculation of the moment of inertia of a thread respect to asse a

 

99) Shape differentiates to delineate them or 1-forma:

It is the associated linear shape to the vectorial field F1(x, y, z)i F2(x, y, z)j F3(x, y, z)k it is worth w = F1 dx F2 dy F3 dz

the vectorial product between the force and the infinitesimal movement can therefore be thought as and represents therefore the job completed from the force in order to move its point of application.

 

100) curvilinear Integral of 2ª species:

It is the job that the F field completes in order to move its point of application gives to in b.

Its value is independent from the parametrizzazione on condition that features of equivalent parametrizzazioni that is that they maintain the direction.

 

101) Shape differentiates to delineate them chiusa:

w sluice if rot F = 0 or in other words is said if the field is conservativo. For De Blasi instead it is had that

w = F1 dx F2 dy F3 dz is sluice if Xy = Yx, Yz = Zy , Xz = Zx .

 

102) simply connected Entirety:

With and simply every curve is connected if sluice in contained it is limited frontier of with entire contained in and that is if every curve sluice can be deformed until to ridurla to a point remaining to the inside of together.

 

103) Shape differentiates to delineate them esatta:

w it is said exact if a function exists upgrades them U that is primitiva of w ossia F = `U from a practical point of view must be controlled that w it is sluice that is that rot F = 0 after which if the dominion is simply connected, then w it is exact while if it is not then w it is exact only locally.

104) integrating Factor :

Integrating factor of a shape is defined differentiates to delineate them w not exact one function m such derivabile that m w is exact, in the plan is always possible to characterize such integrating factor.

 

105) As to calculate the function it upgrades them U:

Us it must before be assessed that w it is exact after which the following formula is applied :

 

106) Way camm(a, b):

It is with of all the distances that combine the point to with the point b.

 

107) Way poligonale cammp(a,b):

It is with of all the poligonali that combine the point to with the point b.

 

108) conservativo vectorial Field:

A vectorial field is said conservativo if a function exists upgrades them U whose gradient is F ossia `U = F .

 

109) irrotational vectorial Field:

A vectorial field is said irrotazionale if rot F = 0.

 

110) radial Field:

It is a field whose value depends solo from the distance from the origin, is a conservativo field, admits that is upgrades them.

 

111) stellato Entirety:

With and it is said stellato if a its 0 point existsp such that the segment of straight that it combines it with whichever other point of the entirety entire is contained in and.

 

112) Calcolo of areas by means of the theorem of Gauss Green:

 

113) Formula of Stokes in the plan:

It is simply a vectorial formulation of the formula of Gauss Green, has :

being T the tangent payer to the delimiting curve D that is obtained deriving the parametrizzazione.

 

114) Formula of the divergence in the plan:

This from the theorem of Gauss Green placing P in place of Q and - Q in place of P obtaining to the first member integral of surface of one is obtained also divergence and to 2° the member the circuitazione of the product to scale between the F carrier and the outgoing normal payer. In formulas it is had :

 

115) Surface:

A surface in "3 is one brace (S,r) being 3 S with of " and r one its parametrizzazione.

 

116) regular Point of one surface:

A point p = r(u0 , v0) says to regulate if the matrix has rank 2 that is is possible to characterize one cartesian representation of the same surface.

 

117) Dominion slowly of Jordan:

T is a delimited limited dominion from a oriented simple circuit g said edge of T

 

118) positive Edge of a dominion of Jordan:

Positive edge is what it unanimously sees the tidy brace(t,n) constituted from the tangent carrier and the oriented normal carrier to the tidy brace of versori the i, j of the plan. An other definition is that the surface must always be covered with the normal carrier towards together.

 

119) Surface sluice:

Surface without limited edge and in " 3 isone .

 

120) regular Surface to pieces:

It is a regular surface for which they exist an ended number of regular curves g 1at times ..., gn contained in S that subdivides it in a number ended of superficial regular said faces.

 

121) co-ordinate Lines of one surface:

u it is the curve that is obtained from the parametrizzazione r(u, v) where v are constant. The tangent carrier is ru(u,v).

v it is the curve that is obtained from the parametrizzazione r(u, v) where u he is constant. The tangent carrier is ru(u,v).

With this representation it can be established if the surface is to regulate verifying that it is ru ^rv = 0.

 

122) Parametrizzazioni equivalent:

Are 2 parametrizzazioni tied from a change of parameter with determining positive jacobiano.

 

123) Equation of the tangent plan to one surface in a point:

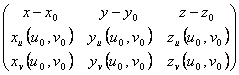= 0

 

124) normal Carrier to one surface:

It is the carrier given from vectorial product ru ^ rv .

 

125) normal Payer to one cartesian surface:

He gains himself from rx ^ ry dividendolo for its norm obtains :

 

126) Towards of the outgoing normal payer in the superficial parametrizzazioni of cartesian:

The external normal payer is directed towards the high.

 

127) adjustable Surface:

A surface is said adjustable if regular and it is taken to a whichever closed circuit and a P point on it, the normal carrier covers with continuity the circuit closed and ripresenta in the P point with the same guideline. The not adjustable cases more drammati us than superficial are the tape of Mobius and the wineskin of Klein.

 

128) Area of one surface:

 

129) Integral of surface of one function h(x, y, z):

 

130) Coordinated of the barycentre of one distribution of superficial mass:

 

131) Centroide:

Draft of the barycentre in the particular case in which the distribution of mass he is constant.

 

132) Moment of inertia of one distribution of superficial mass:

 

133) 2_Forma :

It is a shape of tipo the w = X dy^dz Y dz^dx Z dx^dy

 

134) Flow of a carrier through one S surface :

 

135) simply decomposable Dominion:

T ? "3 are a dominion of simply decomposable Jordan if T is connected and turns out to be union disgiunta of an ended number of simple dominions of Jordan.

136) solenoidale Field:

A vectorial field F is said solenoidale if its divergence is nulla div F = 0.

 

137) or superficialally strongly connected connected Entirety:

An entirety is said superficialally connected if every surface at times contained regular sluice in T delimits a contained limited dominion all in T.

 

138) Formula for the calculation of upgrades them carrier :

F = F2j F3k where e

 

139) As to use the theorem of the divergence for the calculation of the volumes:

y j z k are necessary to consider the vectorial field F = x not campo the F = j k which it gives back always a volume 0.

 

140) solid Angle:

It is dS a surface element and we combine all the points of the contour of dS with the origin Or coming in such a way to form a cone. The intersection betweena center sphere is hour d W Or and beam r and the previous cone ž the solid angle dw is characterized from the relationship between this area and the square of the distance from the origin being therefore the solid angle is .