1) Describe the vectorial space Rⁿ :

It is the cartesian product of the R entirety of n the real ones for if same n times that is Rⁿ = R * R * R *.... * R.

In particular a carrier comes represented with its coordinates reported regarding the origin, such origin can vary to second of the value of n.

For n = 2 we find in R² that is the cartesian plan Or.

For n = 3 we find ourselves in R³ that is in the space Or.

For n = 4 we do not succeed to imagine that space kind represents, however Or.

 

 

2) real vectorial Spazio :

A vectorial space is defined real if in it the following operations are defined:

1) Is in present it element 0 , draft of a having carrier all the coordinates with coefficient 0.

2) Addition of vettori ž is carried out graphically with the rule of the parallelogramma and practically

= = draft of a carrier of the outgoing plan from the origin and culminating in the point of coordinated abscissa = 3, ordered = 8.

 

For the sum moreover the 4 property or axioms are defined following:

a) ASSOCIATES Vto YOUTo ž " x, y, z ? V x y z = (x y) z = x (y z)

b) COMMUTA YOUVTo ž " x , y ? V x y = y x

c) ZERO ž " x ? V x 0 = x

d) CARRIER OPPOSTO ž " x ? V $ x¹ ? V : x x¹ = 0

3) the multiplication between carriers is an operation that in Rⁿ does not have sense, instead is used the multiplication of a carrier for climbing, and it executes moltipicando all the coordinates of the carrier for that one to climb l.

5= =

 

For the multiplication moreover is defined having followed the 4 property or axioms:

a) ASSOCIATES Vto YOUTo ž " x ? V, "l , m ? R x (lm) = (xl)m = (xm)l

b) DISTRIBUTIVE SUM SCALARI ž " x ? V, "l , m ? R x (l m) = xl xm

c) DISTRIBUTIVE SUM VETTORI ž " x, y ? V, "l ? R (x y)l = xl yl

d) UNITA' ž " x ? V x * 1 = x

R[x ] = Polynomial with complex coefficients of variable the x is one typical R spaceⁿ with n equal to the degree of the polynomial .

 

All how much we have said for Rⁿ is applicable also to Cⁿ with the only difference that in the definitions will have to be replaced l , m ? Rⁿ with l , m ? Cⁿ being C, with of n the complexes, therefore the product and sum operations will go second executed asserted how much for n the complexes.

C[x ] = Polynomial with complex coefficients of variable the x is one typical space Cⁿ with n equal to the degree of the polynomial same.

We have demonstrated that the property of the axioms are verified in Rⁿ .

 

2) Product to climb in ⁿ:

Having to disposition 2 carriers, to multiply one for the other does not have some sense, but it has instead sense to execute the product to climb of the 2 carriers, this is obtained executing the sum of the products orders you of the single elements of the carriers

v: = , w: = < v,w > = (-1*4) (1 * 3) (4 * 6) (3*1) = 26

As famous the product to escalate itself represents a n° whose meant it is deduced from the following design:

^{b = p/2} 

That is the product to climb is not that the n° for which we must multiply the carrier w affinche it is along how much the orthogonal projection of v on its director.

The product to climb for being such must have the following property:

1) Commutativa < x, y > = < y, x >

2) Distributiva < x, y z > = < x, y > < x, z >

3) Omogeneità l * < x, y > = < lx, y > = < x, ly >

4) Positività < x, x > > = 0

In particular therefore the product to climb is in a position to dirci if 2 carriers are orthogonal, in fact in such case the projection will be null and therefore also the product to climb.

 

3) Norm:

The norm intimately is tied to the concept of vectorial product, represents also it a n° to climb that this time is not legacy to the projection of a carrier on an other bens¬ to the length of a carrier, second said how much is easy to subject it to the Theorem of Pitagora from which it draws numerous property but of which consequence only in the case is directed in which it comes considered an angle of p / 2 between 2 carriers.

The norm always comes reported to an only carrier.

|| x || = =

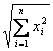
that is it is equivalent to the root of the product to climb of the carrier for if same and therefore to the root of the sum of the squares of the single elements of the carrier. The norm must possess the 3 following property immediately descendants also they gives the product to climb:

1) || x || > = 0

2) || l * x|| = | l| * || x ||

3) || x y || < = || x || || y || ; this is directly the theorem of pitagora in which the hypotenuse the triangle non is sure smaller of the others 2 sides otherwise would be closed.

The third property is daughter of the inequality of Cauchy - Schwarz that says:

| < x, y > | < = || x || * || y ||

 

 

4) Sottospazi Vectorial:

Chosen a sottoset of vectorial space V , it can be or less a sottospazio vectorial, it it is in the case still are verified the property that distinguish a vectorial space that is:

1) Presence of the 0.

2) Sum between carriers.

3) Multiplication of a carrier for one to climb.

In a generalized manner but a short system exists also in order to verify if a sottoset of a vectorial space it is a sottospazio vectorial, must that is be satisfied following:

W ? V is one sottospazio vectorial se " w₁ , w₂ ? W e " l , m ? R

also lw₁ mw₂ ? W

This system is completely equivalent to the first one in how much to riconducibile it, in fact:

case 1) can be placed l = m = 0

case 2) can be placed l = m = 0

case 3) can be placed w₁ o m = 0

In particular:

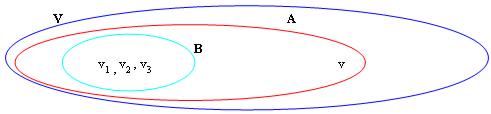
the sottoset is smallest sottoset and belongs to every vectorial space.

sottoset V is largest sottoset and belongs to every vectorial space.

 

5) Constructions generate them of sottospazi:

We begin defining a linear combination as a carrier constituted from the product of k carriers pertaining to V vectorial space with i coefficienti to₁..., to_k. It is introduced therefore in the shape:

3v₁ 5v₂ 2v₃ ... 14v_n

To carry out the Span of one carrier v ? V vectorial space means to generate a sottospazio of the same one, this happens as an example semplicemente thinking next to the multiples of a same carrier, but more in a generalized manner, having 2 carriers the Span represents all the possible linear combinations of the same ones that is the sum of the products of the single carriers for the respective coefficient to_x everyone of i which can assume whichever value pertaining to ".

To notice that affinchè the span it is a sottospazio must be verified the conditions of the short criterion or the long criterion of location of sottospazi, that is:

Criterion lungo: 1) Presence of the 0.

2) Sum between carriers.

3) Multiplication of a carrier for one to climb.

Short criterion: W ? V is one sottospavio vectorial se " w₁ , w₂ ? W e " l , m ? R

also lw₁ mW₂ ? W

A typical example of vectorial space is that one described from a homogenous system, that is having all famous terms = 0;

the span of a similar vectorial space it is gained simply finding the solutions of the system through the reduction of Gauss. These solutions can therefore be written like linear combination more carriers. Example:

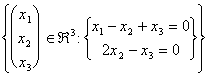
It asks to determine us the sottospazio vectorial in "³ constituted from all the possible solutions for this system which can generally are written like Span of a n° of variable carriers between 1 and n.

As saying previously in order to resolve the system applies Gauss to the associate matrix:

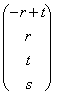
draft of a system already to having scale with one incognito free solution in the carrier:

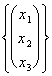= this last carrier can also write r *

This last shape says to us that this sottospazio of "³ can be described like Span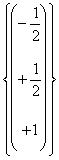

that is it is a vectorial space constituted from all multiples of this carrier that are obtained to varying of r that is of the free incognito that is associated to x₃.

The case exists naturally also in which the Span it is constituted from more than a carrier and this always happens when the solution of the system of equations previews more than one incognito free. In particular the n° of carriers of the Span he is equal to the n° of the free incognito in fact ognuna will go to multiply a carrier and in that carrier us they will have to be the coefficients of this free incognito associates you to respective the x while for the others x the coefficients in the carrier in issue will have to be all 0.

As an example it is supposed to find in a system the following solutions:

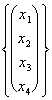= = r s t

and therefore:

= Span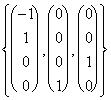

It is from noticing that the Span is a generator of vectorial spaces that can be determine the proportions also in excess, that is is possible to add to the Span as soon as written also an other carrier that if not is also ricorsivo but that it minimally does not alter the definition of Span that has been enunciated.

 

6) linearly independent Carriers, employee, concept of base and dimension:

Leaving from the previous example and the limitation that we have said is implicit in the Span, wonder how many carriers to us are effectively necessary in order to describe a vectorial space?

The answer is similar to the concept of divisibilità of n^{the 1} that is has necessity of n first that we analogous know to be indivisible and generating of all the others numeri. , we has need of a base that is of n carriers through which to construct to all the other carriers of the plan as combination lineare.

Base of an ordered vectorial space is defined therefore with of carriers v_1...,v_t of V such that:

1) Span { v_1...,v_t } = V.

That is the Span must be in a position to describing all V

2) the carriers v_1...,v_t are between independent they.

That is us they do not have to be relations between 2 or more carriers of the Span, as an example cannot be one multiple of the other. In particular in the linear combination they will have to be the 0 all coefficients l , therefore in fact we are only sure that not there is some relation between the carriers taken in consideration.

If also one of the coefficients l is only various from 0 then in the Span is of the redundant carriers therefore the carriers is not all linearly independent and therefore they are defined linearly employee.

Moreover Dimension of a vectorial space V is defined, dim(V) the n° of carriers of which the base is constituted.

It is just this as soon as enunciated the characteristic that differentiates the vectorial spaces regarding the base, in fact every vectorial space has a base but the 2 following cases can be introduced:

1) vectorial Spazio much large one ž Is the case of polinomi "[ X] = a bx¹ cx² .... txⁿ , in they the base exists but it has infinite dimensions.

2) Spazio with dimension finita ž infinitely Has a n° of bases, that is all the carriers that are between of independent they, however we know that the dimension of these bases must be equal for all.

Dimostrazione: is proceeded for absurdity dimostrando that 2 bases with various dimension belong to the same vectorial space, in order to make it writes the carriers of the large base like combination to delineate of the carriers of the small base.

To this point in order to demonstrate that the created carriers therefore are not independent, I collect all the coefficients in a matrix and I become account that the n° of equations is inferior of the n° of incognito, therefore will be of the free incognito that undoubtedly correspond to a dependency of the carriers in issue between of they, therefore did not be a matter of one base various but of the same base.

We have already seen like gaining a Span, we see hour like assessing to us that the carriers of the Span are linearly independent. As an example we have the following carriers ? "⁴ :

, , ,

that they can be written like one linear combination:

l₁ l₂ l₃ l₄

that it gives life to the associate matrix:

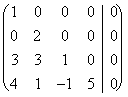which gives like solution =

Therefore the carriers are linearly independent and could give place to a base of the considered space.

if instead the matrix he had been following:

that reduced becomes

that is a matrix with an equation that is cancelled and that therefore it gives to life to one incognito free which renders the carriers of the linearly described Span employee this is necessary but always to demonstrate obtaining it a case in which the linear combination it is 0 but they are not the 0 all coefficients l. Therefore:

= r and therefore placing r = 1: - 1 - 2 1 1 =

We have demonstrated that a solution where the l 0 are not all = satisfies the system equally therefore these carriers is linearly employee and they do not represent therefore one base.

You notice geometric meant following:

Linearly independent

* 2 carriers in "² are independent if they have various directions

* 3 carriers in "³ are independent if they have distinguished directions

Linearly employee

* 2 carriers in "² are employee if they have the same direction

* 3 carriers in "³ are employee if they have the same direction or they are found slowly on the same one.

* 4 carriers in "³ cannot that to be linearly employee

 

7) Affirmations on which the search of one is based base:

to) E' an entirety Massimale that is constituted from carriers between of independent they who become employee if gliene she comes added 1.

 

b) a base is a typical case of with massimale

Dim: we take a B base of V, we add one carrier to it of V and we notice that the carriers therefore obtained are linearly employee in how much if we write this carrier v as linear combination of the others and then from 1° the member we carry it to the 2° we become account that it has coefficient 1 while the other carriers have all coefficient 0.

c) If V = Span (a) and B ? To it is with massimale then is also V = Span (b)

it is demonstrated observing that if is one carrier v that does not belong to B, then it will be able itself to be written that is like linear combination of the carriers in B and To? Span(B) and therefore will be also V = Span(B).

d) Every vectorial space that contains an ended system of generators admits one base

Dim: ž is V = Span(A):

d1) V = { 0 } then V do not have base

d2) we confront v₁ with all the other carriers, if they are all employee comparisons then the base is v₁ altrimenti we take the comparisons that they have given like result of the independent carriers, we as an example have 2 carriers v₁ and v₃ that are independent and candidates to being a base, then we confront them with all the other carriers with which v₁ had been revealed independent, and if also these 3 carriers are independent then we continue to confront with the other carriers that it confronts to you with v₁ had data outcome independent. We reach the base when we find of the employee carriers, the base are all the carriers less the last one considered. If the carriers are in n° exorbitant, the base exists but the comparisons are in n° exorbitant also they and the base, hypothetical infinite.

 

8) Completion of the base:

One base of V is B constituted from n carriers and in V independent carriers are present m then can say these m carriers of V with to n - m carriers of B form one base of V.

Dim: ž the demonstration is according to the induction principle, happens that is before for 1 carrier and then we extend it to all the carriers:

to) We suppose of having in V the solo w₁ linearly independent one regarding if same. We write like linear combination of the carriers of the base, w₁ =  l₁v₁ l₂ v₂ l₃v_{3 ...,} l_nv_n we notice that affinchè w_{2 1} ¹ 0 in how muchis independent must be m all the l is equal to 0 being one base. but if w₁ ¹ 0 then also one of the l must be various from 0 for being able to verify the equality, we suppose that ₁ isv and we according to rewrite equation v₁ dividend for l₁ according to member. To the obtained equation therefore we replace to w_{the 1} its linear combination and obtain that affinchè ₁ ¹ 0 is truehaving place l, will have to be 0 the coefficient for which it is multiplied, that is the coefficient of w₁ therefore i carriers m₁w₁ m₂ v₂ m₃v_{3 ...,} m_nv_n they are one base of V in how much B ? Span(w_1, v₂ , v_3, v_n).

 

b) analogous Reasoning is completed in order to demonstrate that that is worth also for m independent carriers of V that do not make part of the base. The conclusion is that n° of carriers of the base and therefore the dimension of V does not remain unchanged, is for that speaks about completion of the base.

 

From this demonstration we draw numerous observations:

A) the bases of a vectorial space have all the same dimension, why if one had little carriers, gliene could add from an other, but being the massimale base for definition, ci² it would be an absurdity, the only situation that respects the massimalità of the base is the parity of the n° of carriers between bases.

B) Having a vectorial space with dimension n, its sottospazi cannot have dimension m > n.

We see hour like carrying out the completion to one base:

We make the case to have 2 following carriers v₁ = e v₂ =and of wanting to complete them to a base of "³ , we can choose one of the carriers of the canonical base, but to which it guarantees us that the carriers are still between of independent they:

Gauss for columns, that is for carriers us schiarisce a Pò the ideas, we see the Span puts into effect them of v₁ and v₂ and we try to make some osservazione: draft of a system in shape to scale, therefore these 2 carriers are independent, are very clearly that the only carrier of the base that concurs to maintain this scale structure unchanged is the carrier and₃ therefore like segue: and therefore this are one base of "³ constituted therefore from 3 independent carriers, whose Span is all "³ .

9) Spazi vectorial: sum, intersection, complement:

We have analyzed which sets stiche operations can be executed having 2 sottospazi, W1 and W2 of vectorial space V.

W1 ? W2 ? V ž the intersection of 2 sottospazi vectorial is still a sottospazio vectorial of V.

A particular case of intersection is that one between with and its complement, such intersection must be {0}.

We make hour an example on as calculating the intersection between 2 you space vectorial, to such aim is supposed of having the 2 following Span of "⁴ V =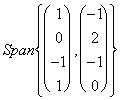 e W =.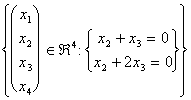

The intersection that interests to us, we can characterize it directly setting up that the carriers of W, beyond answering to the detailed lists supplied from the 2 equations, also are contained in the Span of V.

We reassume therefore the carrier of the coefficients l and m for V, draft of the carrier of the solutions:

if hour we replace x₂ and x₃ in the definition of the carriers of W we exactly find the intersection between the 2 sottospazi. from which we gain l = m = 0 and pertanto .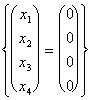

That wants to say exactly that between the two sottospazi not there is some intersection therefore dim(the V ? W) = {0}.

W1 ? W2 ž is not always a sottospazio vectorial of V, tasks to the case of W1 = Span of the carrier of the flat and W2 = Span of the carrier, they represents makes us of straight between orthogonal they, then if we take 2 carriers and of it we make the sum with the method of the parallelogramma, such sum will turn out to be a carrier with various direction regarding all the others, therefore the sum is not contained in V and therefore the union of 2 sottospazi of V not necessarily is one sottospazio also it.

W1 W2 ? V ž the sum in a generalized manner replaces the union and is always a sottospazio vectorial.

A particular case of sum is that one constituted from 2 sets of which one is the complementary one of the other, with this condition only can assert that the sum is written in an only way, such sum comes then defined directed.

In the case that the intersection of the 2 sets is various from { or } then there are more ways than to write the sum like in the following case: the following carrier is had in "³, it can be written = =

We make hour an example on as calculating the dimensions of the sum of 2 you space vectorial, we place are following the Span of "⁴ V =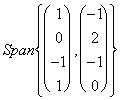 e W =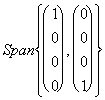uno of the methods in order to calculate of the sum is to join them in an only matrix and to see if they are independent carriers, therefore like it follows:

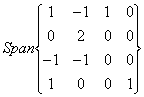Such control in such case goes made for columns, be a matter itself of carriers and not of equations.

However more express to second is also a way of the problem, that is to put into effect the formula of Grassmann, is clearly that they must be known is the dimension of V, of W and also of theirs intersezioneed applied to following:

Dati 2 sottospazi vectorial U and W of V, is valid the following relation: Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

Tobbiamo 2 generators, 2 B and C of sottospazi U and W, we can say that B then ? C is with of generators of U?W. However we are speaking only about Span and not about bases, in fact the union of 2 bases could also characterize of the carriers that are not independent

 

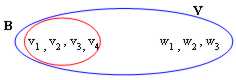
10) With complementary:

It is defined with complementary of To, such the B entirety that does not have some intersection with To and that the all forms the vectorial space B according to the successive design:

We make to this point an example on as to find a determined complement of sottospazio a vectorial one of a space V.

In the example on the completion of the base, we had seen like completing i two carriers v₁ = e v₂ =to one base of "³, and the result was the tern of vettori: therefore can say that one having complement ofv ₁ dimension 1 is the plan generated from the carriers . Analogous the complement in "³ of the plan generated from i carriers v₁ and v₂ is the having carrier dimension 1.

11) Theorem of Grassmann:

Dati 2 sottospazi vectorial U and W of V, is valid the following relation: Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

That the dim of the sum it is not all intuisce also visually being believed that in the sum they come eliminates all the carriers to you that in some way are redundant in the single dimensions of the sottospazi. Those somewhat is represented from the intersection.

Demonstration:

We have uv₁ uv_n that it is a base, we complete it in U to uv₁ uv_n u_{n 1} u_p and in W to uv₁ uv_n w_{n 1} ws

We must demonstrate that the carriers u that they are completion of the carriers uw in U

the carriers w that they are completion of the carriers uw in W

the carriers u that they are in the U intersection ? W =

base of U W must be one that is its Span and between independent they

affinchè that is true must be p (n-p) (s-p) = n s - p = dim(U W)

what is equivalent to dire: Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

therefore B must be {uv₁ uv_n u_{n 1} u_p w_{n 1} ws} and affinchè he is independent all the coefficients (than they are not written) must be = 0. We demonstrate observing that " v ? (U?W), " u ? (u) and " w ? (W), but for essere w v u = 0 ž w = - v - u ž therefore w stà in (U?W)e can therefore be written like linear combination of v, but w he is also equal to uv₁ uv_n w_{n 1} ws that therefore they must be also independent they in order to verify the equality, therefore w therefore all the coefficients of B are 0.

 

A lot interesting for mnemonic the example made from Schoof. V are supposed a plan and W an orthogonal plan to it therefore both with dimension 2:

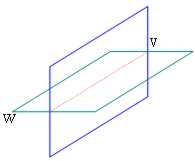
As it can be noticed, the intersection between the 2 plans is one straight having dim = 1

therefore dim(V W) = dim(V) dim (w) - dim(V ? W) = 2 2 - 1 = 3

and in fact 3 is exactly the dimension of the space.

 

12) direct Sum:

Directly from the theorem of Grassmann the theorem comes down the definition of direct sum in fact says:

Dim(U) Dim(W) = Dim(U W) Dim(U ?W)

And from this famous good that if the intersection between 2 sottospazi vectorial is null, then the dimension of the space sum is exactly equal to the sum of the dimensions of the spaces addends:

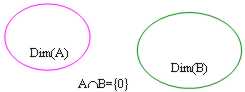
in formulas Dim(A B) = Dim(A) Dim(B)

and in this case therefore the sum is defined direct and been possible to write it in an only way as already enunciated.

 

13) linear Applications:

We have analyzed the case in which to a vectorial space it comes applied a function and the image of this function we have it in an other vectorial space.

We have endured defined an application like delineating if following are defined:

Addizione f(v₁ v₂) = f(v₁) f(v₂)

Moltiplicazione f(lv) = lf(v)

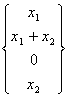
Therefore we have made the example of one application in V ? "³ having values in W ? "² that is

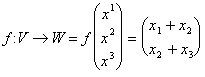we must verify if it is to delineate that is the 2 criteria:

a) f(v₁ v₂) = f(v₁) f(v₂)

1° the member vale:

2° the member vale: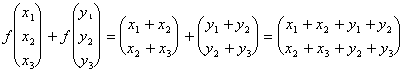

evidently the two members are equal therefore draft of one linear application regarding the sum.

b) Moltiplicazione f(lv) = lf(v)

1° the member vale: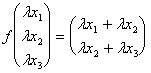

2° the member vale: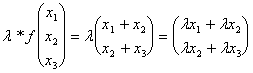

evidently the two members are equal therefore draft of one linear application regarding the product.

 

A short criterion exists then also in order to determine if an application is to delineate that it derives directly from the short criterion for the determination of the sottospazi, that is:

criterion breve:

 

14) Image of the function applied to a vectorial space:

The image is defined like the carriers w ? W: one carrier v in V exists: f(v) = w

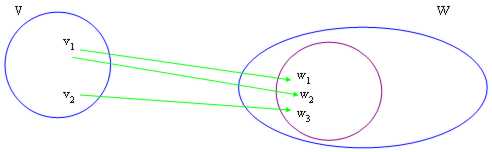
We have then demonstrated that Im(f) is a sottospazio of W and that for definition, if the image of f is all W then says that f it is suriettiva, memories that all the cowboy come hit from at least one arrow.

For the calculation of the dimensions of the image they must naturally be found the solutions of the system tax from the function and being in n° limitless, to express them like one Span of some carriers. It is supposed as an example of having to find the solutions of seguente: the

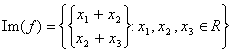
from which 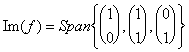that is equivalent to matrice the Span

that reduced diviene: Span in which looks at that a carrier was combination for delineating of the others 2, for which we can say that Im(f) = Span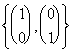 and has dimension 2.

 

15) Nucleus of one linear application:

Instead nucleus of a linear application or Ker(f) is defined all i carriers v in V that end in the 0 of the image

 

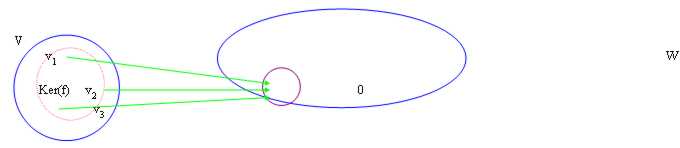
We have then demonstrated that Ker(f) is one sottospazio of V.

 

16) a function applied to a vectorial space is iniettiva if ker(f) = {0} that is if not there are carriers in the nucleus:

The demonstration is subdivided in 2 parts:

 

to) Knowing that f it is iniettiva, we try to assert that Ker(f) = {0}ossia that the nucleus is empty.

We take one carrier v ? Ker(f) and we say that it must be f(v) = 0 being the iniettiva function, we can but assert that f(0) = 0 and therefore v = 0 that is the carrier do not exist.

 

b) Knowing that the nucleus is empty I must demonstrate that f it is iniettiva that is that every cowboy single arrow is hit from one.

I take 2 arrows, x and y and demonstrate that they hit 2 cowboys different f(x) and f(y), if they hit the same one cowboy f(x) = f(y) then were same arrow x = y. is demonstrated taking advantage of the linearity of f saying that it must be f(x) - f(y) = 0 in how much we suppose f(x) = f(y) and we want to succeed in to say that x = y.

Applying the linearity we deduce that 0 = f(x - y) but the nucleus must be empty therefore x - y = 0 that is x = y.

We see to this point as the nucleus is estimated ker(f), turns out enough intuitivo to think that we must find all the solutions of the function that are worth 0, therefore we reduce ourselves to the study of a homogenous system.

It is supposed of having to calculate the dimensions of the following nucleus of application f: "³ in "².

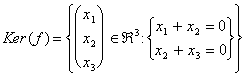equivalent to matrice the

Draft of a system that normally must be resolved through Gauss for columns but in this case is already in shape to scale and has 2 equations for 3 incognito, therefore one incognito is free and already intuiamo that the dimension will be 1.

In particular: 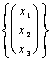= this last carrier can also write r * from which implicitly it follows that: Ker (f) = Span.

 

17) representative Matrix of one linear application:

The representative matrix completes an operation that various would seem somewhat complex, it receives as income a containing base of the vectorial space the dominion, a containing base of the vectorial space codominio and the function that alloy dominion and codominio, and supplies like escape a way express in order to calculate the value of the image for a any carrier of the dominion.

Normally as bases choose those canonical ones, however nobody prohibits to use bases whichever purchè ended therefore as the spaces from they generate to you.

The explanation of as they are gained and dialtri terms will come dynamically supplied; we see as such the following matrix for application is gained to delineate:

g: "³ ® "² : g =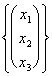= we must in the first place control that this application is to delineate that is that the 2 following equalities are respected:

1) g(v₁ v₂) = g(v₁) g(v₂)

2) g(lv) = lg(v)

We choose hour one base for "³, naturally that canonical and₁ = , and₂ = , and₃ = .

Analogous we choose hour one base for "², still that one canonica f₁ = , f₂ =.

To this point we have all and we can therefore pass to describe the construction of the representative matrix of g regarding the 2 used bases.

The columns of the representative matrix in fact are constituted from the application of the function g to the constituent carriers the base, that is and₁ , and₂ , and₃ . In our example, g(e₁) =, g(e₂) = , g(e₃) =

and the representative matrix is therefore: .

where the n° of columns he is equal to the dimension of the dominion and the n° of lines he is equal to the dimension of the codominio.

To this point we are in a position to calculating what easily simply happens to carrierv ₁ = when to it we apply the function g, carrying out the product between the rappesentativa matrix and this carrier:

*= where 5 are obtained multiplying 1ª the line for 1ª the column while 7 the normal multiplication of a carrier for one is obtained multiplying 2ª the line for 1ª the column second matrix.

Naturally the same result could be obtained replacing carrier v ₁in the description of the function directly, however for great calculations the better procedure is this hardly illustrated.

You notice yourself that the obtained carrier therefore goes meant like a carrier of coordinated regarding the base f the supplied one for the codominio.

It is intuitivo to gain that knowing only the representative matrix the function can be gained simply multiplying such matrix for the generic carrier of dominio: the *= .

Rank of a matrix is defined the dimension of its image, in this case the rank of the representative matrix is found, finding of the image that is with of the solutions that as we have seen express in terms of span and the carriers that make part of the span must be all independent ones, however a function cannot be spoken about a base in how much is a restriction of with and therefore the Span cannot be all with therefore like instead would have to be for one base.

 

18) representative Matrices of composed functions:

The concept of composed function is very famous and is riepilogato in figure:

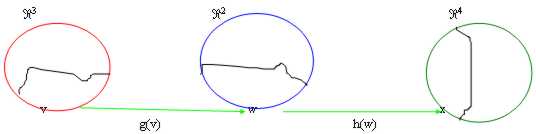
It is supposed:

g: "³ ® "² : g == whose representative matrix is: .

h: "² ® "⁴ : h =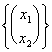= whose representative matrix is: .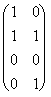

The representative matrix of the composed function h ° g is the product of the 2 representative matrices:

h ° g = *=

To analogous result but in more arduous amniera it was reached replacing the function the two generic elements of the function

g = in the function h = reaching the h ° g =

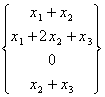
that applied to the carriers of the base of "⁴ and₁ = , and₂ = , and₃ = , and₄ =

it supplies the same previous result ossia: exactly h ° g = .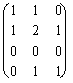

In composing a matrix must be attention to comprise in particular if it is a sensata operation or less, must

to be with of passage of the same dimension in arrival regarding the dimension in departure, practical:

composition "² is possible ® "⁴® "³

but composition "² is not possible ® ("⁴ "¹)® "³

In fact a writing of the type ( "⁴ "¹) does not have sense.

 

19) biiettive linear Applications:

A function as we know is biiettiva when is is iniettiva (every element of the image can be function of an only element of the dominion) that suriettiva (the image is all the codominio).

the biiettività interests to us fundamentalally why it it condition affinchè a representative matrix of the function g is invertible that is exists the inverse one g^-1.

The first prerogative of an invertible matrix is that it is square that is that the n° of lines is equal to the n° of columns.

The procedure in order to calculate it is following:

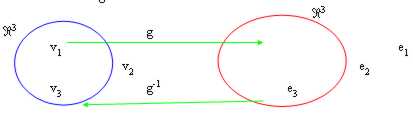
from the illustration it is comprised well that our scope is to characterize those elements v the whose image is _{the i} and base codominiothat is , that is obtained resolving linear system g(v_i) = and_i.

One supposes that the representative matrix is: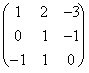then the linear system is:

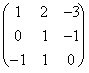* = and₁ = ž = that it is 1ª the column of the inverse matrix.

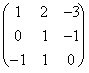* = and₂ = ž = that it is 2ª the column of the inverse matrix.

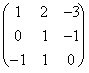* = and₃ = ž = that it is 3ª the column of the inverse matrix.

therefore the inverse matrix of the representative matrix 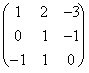is the matrix .

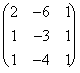You notice yourself that the following matrix could be reached the same result resolving:

in order to obtain to right the inverse matrix I must try to reduce the matrix of left to a diagonal matrix therefore as at the moment it is to right.

We begin reducing to a system to scale: 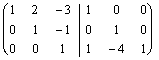and then leaving from the pivot low, we create the 0 over all pivot with the usual method of Gauss, we obtain: 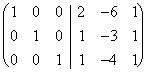that, to right it introduces the inverse matrix exactly that we tried and is equal to that one found with the long method.

I can moreover control that the obtained result is corrected, in fact if I multiply the representative matrix for the correspondent inverse matrix I must find again the base from which they have left for the definition of the matrix rappresentativa. Therefore in the case precedente: *=

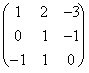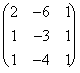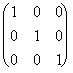
Where the product is executed to the usuals:

1ª line for 1ª column

2ª line for 1ª column

3ª line for 1ª column

1ª line for 2ª column

etc....

3ª line for 3ª column.

 

20) When a representative matrix is not invertible:

We will not know never a priori if a matrix is invertible or less, the only way in order to render of account us is to carry the calculations ahead sin when it is not reached to an absurdity like following: where 3ª the equation says us that 0 are equal to 3 various coefficients, that it is 3 times absurd in how much 0 is equal only to 0.

An other case of absurdity of equations is following: where the 3ª incognito it says us that x₃ must be equal to 1 while 2ª the equation says us that x₃ must be equal to 3, they cannot contemporaeamente be true both, therefore the system does not have solution and that representative matrix is not therefore invertible.

 

21) Change of base:

Hour is supposed to have a representative matrix of "³ set up the canonical base second, and of wanting instead to set up it second following base: the and₁¹ = , and₂¹ = , and₃¹ = .

The representative matrix regarding the canonical base is seguente: the 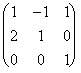must hour to calculate the representative matrix regarding the new base, proceeds observing that the columns are exactly the function applied to the singloli carriers of the base. We proceed therefore:

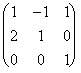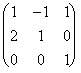f(e₁¹) = *=, f(e₂¹) = *= , f(e₃¹) = *=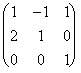

Now I must find which coefficients, multiplies you for the base and¹ gives like result these to me 3 carriers, therefore:

f(e₁¹) = having like soluzioni: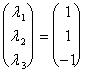

that it is 1ª the column of the representative matrix B regarding the base and¹ Analogous:

f(e₂¹) = having like soluzioni: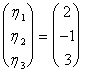

f(e₃¹) = having like soluzioni:

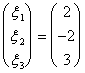
Therefore the representative matrix regarding the new base is.whose columns are carriers f(e₁¹), f(e₂¹), f(e₃¹).