Ortonormali Autovalori and bases
Autovalori
1) Definition of autovalore:
There are of the applications for which to one sure carrier v, through the application a its multiple corresponds, in formulas f(v) = lv in such case the value of multiple v is the autovalore while the correspondent carrier v is the autovettore. To a same autovalore more autovettori can correspond, in such case with of the autovettori take the name of autospazio.
2) When base of autovettori for one exists one application:
For an application a base of autovettori exists when it can be represented respect to one particular base from one diagonal matrix.
3) When an application is diagonalizzabile:
An application is diagonalizzabile when it has all the autovalori on the field and their algebrica variety coincides with the correspondent geometric variety. from that drift that the sum of the geometric varieties must is equal to the dimensions of the space host.
4) To what they serve the autovalori in the calculation of f n = f * f * f.... * f:
They serve to diagonalizzare the representative matrix of the application f, to such point the power is executed easily ennesima directly on the diagonal matrix and finally the change of base of this last one is made using the same formulas.
5) Like understanding to eye from the matrix the autovalori of one application:
Simply they are the values that lower the rank of a matrix, than render it that is not maximum.
6) That type of autovalori has one projection:
A projection is an application that if it comes carried out 2 times gives the same result that is obtained once carrying out it single, in formulas: f(v) = lv f(f(v)) = l(lv) = l2v
Based on how much said lv = l2v and therefore l(l-1) = the 0 therefore autovalori are 0 and 1.
7) When a matrix To and a B matrix can be conjugated:
When one such matrix C exists that B = C * To * Cthe -1 that it only happens on condition that To and B has the same autovalori with the same geometric varieties and the same algebriche varieties.
8) Criterion in order to immediately characterize part of polynomial characteristic of one the matrix:
Il coefficient of the term of degree n is (-1)n while the coefficient of the term of degree n-1 is (-1)n * trace To, finally the coefficient of the term of degree 0 that is the famous term is equal to the determining one of the matrix To.
9) When a matrix is nilpotente and that type of autovalori has:
a matrix is nilpotente when one its power of degree n > = the 1 é null matrix.
the autovalori are necessarily all 0.
Quadratic shapes
10) As the signature of a quadratic shape is found:
The currency is estimated some polynomial characteristic dopodichè if the sign of the autovalori with the method of Cartesio.
11) Enounce the rule of Cartesio for the location of the signature of the solutions of a polynomial :
the polynomial is ordered from the maximum degree to the minimal degree, to such point currency:
n° positive roots = n° of the variations of sign in the polynomial
n° roots nulle = the present minimal degree in the polynomial
n° negative roots = the maximum degree of polynomial - (n° positive roots n° null roots)
Scalari products
12) When a shape is bilinear:
A shape is bilinear when it is to delineate respect to both the variable ones, must that is be verified that
a) f(lv mv1,w) = lf(v, w) m f(v1,w)
b) f(v,lw mw1) = lf(v, w) m f(v, w1)
13) What is a product to climb and which associated matrix is to it:
A product to climb is a such symmetrical bilinear shape that is that f(v, w) = f(w, v).
The associated matrix to it is one symmetrical, such matrix that is that the element toij = toji .
14) Definition of product to climb canonical:
A product to climb canonical is positive a defined symmetrical bilinear shape, is worth to say that < v,v > it is > = 0 and < v,v > 0 La associated matrix to it is = 0 > v = is one determining symmetrical matrix with positive.
< v,w > = v1 *w1 v2* w2 ...... vn * wn
15) Typology of scalari products:
Defined scalari products positi to you, semidefined exist positi, defined denied to you, semidefined denied to you to you, indefinite, the semidefined scalari products positi to you and denied there are necessarily degenerate that is not only assume value 0 for carrier 0 .
16) As the distance between a point and a sottospazio is found:
It is found gaining the orthogonal projection of the point on the sottospazio and calculating the distance regarding this characterized point. The orthogonal projection can be gained easily which intyersezione between sottospazio and the straight one passing for the point p and having which carrier director the orthogonal carrier to the plan which if the plan has equation ax by cz = d then is the carrier (to, b, c).
Otherwise the distance through the formula can more
quickly be calculated 
It is from noticing that in "n it is worth a logical extension of this formula gaining time for time.
17) < < x, v>v, v>v are equal to < x,v > < v, v>v :
, the passage is authorized person, in fact < x,v > it is to climb and a carrier and therefore cannot be carried externally to the product to climb same.
18) When a shape is to sesquilineare:
A shape is to sesquilineare when the two following property are verified:
f(lv mv1,w) = lf(v, w) mf(v1,w)
f(v, lw mw1) = lf(v, w) mf(v, w1)
19) What is a hermitiano product and which associated matrix is to it:
A hermitiano product is a shape to sesquilineare that it enjoys the hermitianità, is worth to say of the following property:
The associated matrix to it is a symmetrical matrix in which the element toij it is the conjugated one of the element toji must moreover be B = Bt
20) Definition of canonical hermitiano product:
A canonical hermitiano product is a shape to sesquilineare hermitiana defined positive, is worth to say that < v,v > it is > = 0 and < v,v > 0 La associated matrix to it is = 0 > v = is one determining symmetrical matrix with positive.
< v,w > = v1 *w1 v2*w2 ...... vn * wn
21) Like determining if a matrix is hermitiana:
Dever to be B = Bt that it implies that on the diagonal only real elements in how much must be present the transposition leave the diagonal and to = unchanged to > ? ".
22) Characteristic of the matrix associated to a product to scale or defined Hermitiano positive:
They are both matrices having determining positive.
23) Write the conjugated transposed one of 
and saying if it is hermitiana:
Here there is the trabocchetto, in fact the conjugated one
of a n° sees to change of sign the imaginary part and the real part
therefore the conjugated transposed one is not: 
clearly the conjugated transposed one is not hermitiana in
how much is various gives it departure matrix.
Ortonormali Bases
24) It has sense to speak about ortonormali bases without to have introduced the product concept to climb:
In how much they do not have to be constituted from carriers which are orthogonal between of they and this is measurable through a product to only climb which it concurs the measure of angles and distance.
25) Which ortonormale base of autovettori is the main advantage of one:
Creed that the greatest advantage is that the inverse matrix is banally equal to the transposed matrix.
Moreover a ortonormale base is the only one through which it is possible to realize isometrie that is transformations that do not alter angles neither dimensions of the departure object and therefore they do not deform it.
26) Describe the steps of the Ortonormalizzazione di Gram - Schmidt:
to) it is standardized v1 v1 *
b) one becomes according to carrier of the ortonormale base to the first one v2 ' = v2 - < v2, v1 * > v1 *
c) is standardized v2 ' v2 *
d) the third formed orthogonal carrier to the sottospazio becomes from v1 * and v2 * that is:
v3' = v3 - < v3, v1 * > v1 * - < v3, v2 * > v2 *
and) it is standardized v3 ' v3 *
27) That sense has to ortonormalizzare one base:
An application only has orthogonal autovettori if it that is has all distinguished autovalori if to every autovalore corresponds a single autovettore, otherwise the autovettori inherent to the same one autospazio can also not be orthogonal, in such case it has sense to proceed to the Ortonormalizzazione di Gram-Schmidt which beginning from one of the 3 autovettori creates a ortonormale base which succeeds in diagonalizzare with an orthogonal transformation the representative matrix of which we have found autovalori and autospazi.
28) Normalizzare the carrier 
:
The trick is to estimate the norm of all the carrier, then to divide 1/3 for such norm and to multiply for the carrier.
29) Like calculating the projection of a point on the carriers of one ortonormale base:
The coordinates reported to an axis of the base are not
other that the product to scale of carrier v for the payer of the
divided base the norm of the payer who is clearly 1 therefore the
value of the coordinate of a carrier respect to a payer of a
ortonormale base is not that the product to climb of carrier v for the
payer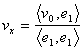 
.
30) Describe the least-squares method for the identification of the straight one of better approximation than a series of data experiences them:
The method given some points concurs to characterize the straight one that better approximates them, to such aim writes the not compatible linear system containing all the generic equations of straight passing for the points you lx m º y in such a way creates a A(x) matrix = b our scope is to project the carrier b on the sottospazio of the solutions of the A(x) system that is on Im(A(x)). This in practical is obtained setting up the equality tTo * To = tTo * b.
To this point the obtained system is a B matrix 2*2 to 1° the member and one carrier c 1*2 to according to member, is resolved with the method of Cramer, that it finds the coefficient of x which the relationship between the determining one of the obtained matrix replacing in B in place of 1ª the column carrier c and the determining one of B. The coefficient of the y finds which relationship between the determining one of the obtained matrix replacing in B in place of 2ª the column carrier c and the determining one of B.
Orthogonal Applications
31) Define one orthogonal application and to describe of the characteristics:
the relation < T(v), T(w) > = < v, w > is worth on the field of the real ones.
the meant one is therefore that it does not come altered metric of the space the image, is worth to say that an object to which we apply a unitary transformation does not come deformed.
32) Like determining if a matrix is orthogonal:
The carriers column of To form one ortonormale base.
a) must be |det B| = 1
b) if it is true a) is controlled that the carriers column have norm 1
c) if it is true b) is controlled that the carriers column are mutually orthogonal
d) optionally to control that Bt * B = Id
33) If I have found for an application 2 autovalori y1 and y2 with autovalori Vy1 and Vy2 standardize to you, as I can diagonalizzare the application and as it is made the matrix diagonalizzata:
I can re-unite the autovettori in an orthogonal matrix of change of base through which the representative matrix is reduced to a diagonal matrix on whose diagonal for the note appears the autovalori.
34) orthogonal matrix for diagonalizzare one Is necessary one representative matrix:
Not, a representative matrix comes diagonalizzata also from a base of autovettori not standardized, the problem is that in such a way a carrier to which we apply the matrappr is various from the carrier obtained making the change of base towards the diagonalizzata shape, applying the matrappr diagonalizzata and then we bring back it in the old base.
Unitary Applications
35) Define one unitary application and to describe of the characteristics:
The relation < T(v), T(w) > = < v, w > is worth on the field of the complexes.
The meant one is therefore that it does not come altered metric of the space the image, is worth to say that an object to which we apply a unitary transformation does not come deformed.
36) Like determining if a matrix is unitary:
a) must be |det B| = 1
b) if it is true a) is controlled that the carriers column have norm 1
c) if it is true b) is controlled that the carriers column are mutually orthogonal
d) optionally to control that Bt * B = Id
37) If the carriers column of a matrix To are an orthogonal base, To it is unitary:
Not, they must be one ortonormale base.
38) When matrix is true for one that B = Bt = B-1 :
When the matrix is is unitary Hermitiana that.
39) Which artifice can be used in order to find the roots of a polynomial characteristic of 2° degree on the complexes:
The famous term is the product of the solutions for which if as an example a solution is and also the famous term is then the other solution is evidently also it i.
40) If in the course of the search of roots of a polynomial
characteristic of 2° degree on the complexes it is met 
as it is decomposed:
is considered
= and it is resolved then carrying -2i in polar shape and applying
the formula of De Moivre for the powers of complex numbers.
Beginning carrying in polar shape -2i.
| -2i | = 
while arg(-2i) =
therefore in polar shape we have 
therefore = 
.
Symmetrical Applications
41) Define one symmetrical application and to describe of the characteristics:
An application is symmetrical when verification that < f(v), w > = < v, f(w) >.
42) As it is made the matrix of one symmetrical application:
It is a matrix for which the element toij is equal to the element toji.
43) That determining us attends from one symmetry :
Det = -1 in fact the isometriche transformations are all and sun the spins and the simmetrie and know that the simmetrie have determining -1.
44) That determining us attends from one spin:
Det = the 1 in fact isometriche transformations are all and sun the spins and the simmetrie and know that the spins have determining 1.
45) When an application is antisymmetric:
An application is antisymmetric when verification that < f(v), w > = -<v, f(w) >.
46) As it is made the matrix of one antisymmetric application:
It is a matrix for which the element toij is equal a - toji , from this it follows that on the diagonal 0 are present single, in how much must be tTo = - A.
47) Describe the anti-Hermitiane matrices:
It is a matrix for which the element toij is equal a -toji , from this it follows that on the diagonal they are present solos you finish with null real part, in how much must be tTo = - To.
Determining
48) If Det To = 7, how much is worth Det (B-1 To B):
It is worth 7 why the determining one is one invariant function for change of base.
49) Enounce the theorem of Binet on the determining ones:
Det (AB) = Det(A) * Det(B).