Questionnaire of physics

1) How much is worth the projection of a characterized payer on the straight one from a payer:

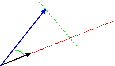To

V

A' = To * costo

Wanting instead to project the carrier along an orthogonal payer to v the projection is To * sento.

 

2) To x ( B x C ) =

B ( To * C ) - C ( To * B )

 

3) ( To x B ) x C =

B ( To * C ) - To ( B * C )

 

4) In order which reason the carriers in physics are used:

The vectorial relations are independent from the particular chosen system of coordinates, and therefore it they are also the expressed physical laws vectorially.

 

5) How many ways are in order to describe the position of a point in the space:

a) gaining of the coordinates which projections on the carriers of the ortonormale base

b) If the point is bound to remain on a plan, the polar coordinates can also be used.

c) If the point is bound to remain on a curve can be used the curvilinear abscissa that is the distance oriented respect to a point of the taken curve as origin.

 

6) What is the trajectory of a point:

It is the geometric place of the positions occupied from the point to varying of the time.

 

7) What is the associated hour law to the motion of a point:

It is the equation that alloy the time to the position of the point on the trajectory

 

8) Define the n° of degrees of freedom of a motion:

It is the n° of independent coordinates that characterize the position of the point p. Therefore if as an example a point of the space is bound to belong to a plan the n° of the coordinates necessary in order to describe of univocamente the trajectory is 2 and therefore also the n° of freedom degrees it is 2.

 

9) Define the carrier D movementr:

Draft of the carrier that combines the position to the time t to the position to time (t Dt).

 

10) Define the carrier medium linear speed v_m :

Draft of the relationship between the carrier movement and the interval in which it is calculated.

 

11) Define the carrier instantaneous linear speed v(t):

It is the limit for Dt ® 0 of the carrier medium linear speed.

Since for an infinitesimal interval it can be confused the carrier movement with the curve arc follows that draft of a having always tangent direction to the trajectory to curve in the point occupied to the moment t and having carrier coinciding module with the temporal derivative of the curvilinear abscissa.

 

12) Describe the carrier medium linear acceleration to_m :

Draft of the relationship between the carrier variation of speed in the interval of D timet and the interval in which it is calculated.

 

13) Define the carrier instantaneous linear acceleration a(t):

It is the limit for Dt ® 0 of the carrier medium linear acceleration.

The direction of this carrier is characterized which sum of one normal member and one tangential member:

Acceleration tangenziale its module is worth and is directed tangentially to the curve.

For a uniform circular motion it is null.

Acceleration normale its module vale and is directed towards the having center of the osculatore circle beam r that is the center of the curve, comes therefore called centripetal acceleration.

 

14) When a motion is said they centers:

When it is carried out on a plan and the tangential acceleration is null.

 

15) What is and when the speed is defined to areolare:

It is a speed defined for the motions only centers them and therefore plans, it identifies itself in an orthogonal carrier to the plan on which the motion happens and passing for the center of the motion it expresses the rapidity with which the elementary area it comes swept in the infinitesimal time.

 

16) Describe the uniform rectilinear motion:

Draft of a motion that happens to constant linear speed and therefore with null acceleration.

 

17) Describe the uniform accelerated rectilinear motion:

Draft of a motion that happens to constant linear acceleration having the single tangential member.

 

18) Define a serious one:

Draft of a whichever body that moves along vertical towards the center of the earth with constant acceleration the due to the interaction of the body with the earth, g = 9,81 m/s².

 

19) Describe the harmonic motion:

Draft of a periodic motion that happens along one single dimension second harmonic a hour law (sento or costo).

Its equation differentiates them is while its hour laws are:

finally the period .

 

20) Describe the carrier elementary angular movement dq:

It is an orthogonal carrier to the plan on which the spin happens and whose module is equal to the entity of the angle swept from the beam carrier in the time unit.

 

21) Describe the carrier angular velocity w :

It is a carrier with the same direction and towards of dq and equal module to the variation in the time of dq .

 

22) Describe the uniform circular motion:

Draft of a motion that happens to linear speed constant that it implies that w its acceleration is constant vectorially is pure normal and is worth . This motion can also be believed as composition of 2 orthogonal harmonic motions and sfasa you of 90°.

 

23) Describe the not uniform circular motion:

Draft of a motion that happens to linear speed not constant that it implies that w its acceleration is not constant vectorially is introduced is normal member who tangential member .

 

24) Define the derivative of a ruotante payer second the formulas of Poisson:

Such result mainly serves in the relative motions you in order to carry out the derivatives of the system of rototraslante reference.

 

25) Enounce and to in motion describe the value of the absolute speed reported to the reference system:

where

is the speed of the material point P measured from the mobile observer.

represents the dragging speed that is the speed that competes to a point of the measured rotary system from the fixed observer.

 

26) Enounce and to in motion describe the value of the absolute acceleration reported to the reference system:

where

is the acceleration of the material point P measured from the mobile observer.

represents the dragging acceleration that is the acceleration that competes to a point of the rotary system measured from the fixed observer having following means to you:

is the relative acceleration to the translation of the origin.

is the tangential acceleration that competes to a point of the measured rotary system from the fixed observer.

is the normal acceleration that competes to a point of the measured rotary system from the fixed observer.

is the acceleration of Coriolis that for the relative observer turns out only deviatrice in how much ^ to v_r .

 

27) Describe one characteristic general of the carriers associates you to the largenesses angle irons:

They are carriers does not apply to you which if the motion is flat turn out orthogonal to the plan on which the motion is carried out.

Dynamics of the point

28) That what is inertia:

It is the tendency of a body not to abandon its state of quiet or uniform rectilinear motion.

 

29) When a reference system is nertial or galileiano:

When it does not supply some action to a loyal body to it.

 

30) Enounce 1° the principle of dynamics or inertia:

In a system of nertial reference a body, not subordinate to some action, continues in its state of quiet or uniform rectilinear motion

 

31) What is a force:

It is the physical cause that modification the state of quiet of a body.

 

32) What is the nertial mass:

It is the measure of inertia of a body to vary its vectorial speed under the action of a constant force. It only varies with the speed for next speeds to those of the light.

 

33) That what ¨ the momentum:

It indicates the difference between the being invested from Moscow or a 10 truck that goes both to Km/h.

 

34) Enounce 2° the principle of dynamics:

In a system of nertial reference the force applied to a body is equal to the infinitesimal variation in the time of its momentum only coincides with the for next speeds to those of the light

 

35) That what ¨ the impulse of a force and how much is worth:

is that is equal to the variation of the momentum in 2 moments considers you.

 

36) Enounce 3° the principle of dynamics:

It is the principle of the action and reaction according to which if two B and bodies interact then

They that is have same module and direction but opposite back.

 

37) Define and to estimate the force weight:

It is an attraction force that the earth exercises on a whichever endowed body of mass is constant directed P = mg and towards the center of the planet, is worth 9.81N.

 

38) Define and to estimate the elastic force:

It expresses the ability that has some bodies like the motivating force to answer to the force to applied it with a deformation, when the body does not act more the external force then stretches to return in the conditions begins them estrinsecando a force proporziona them to its deformation where k it is the elastic constant of the motivating force measured in N/m.

 

39) How much is worth the elastic constant of 2 motivatings force in series:

just like 2 resistances in parallel.

 

40) How much is worth the elastic constant of 2 motivatings force in parallel:

just like 2 resistances in series.

 

41) That what ¨ the force of resistance to the advance:

The fluid is a force in which the body moves opposes to the same motion, it is function of the geometric characteristics of the body in motion where:

to = shape factor

r = volumica mass of the fluid

S = area of the projection of the body on an orthogonal plan to v

f(v) = the resistance is therefore also function of the speed.

 

42) Thing distinguishes the resistance to the viscous advance from the resistance to the hydraulic advance:

The viscous one is worth for inferior speeds to the 2 m/s and is worth while the 2ª it is relative to speed comprised between the 2m/s and the 200m/s and is worth where b in both the cases are the damping coefficient. In both the cases famous that the body in its motion cannot exceed one determined speed adopt a position exactly from this resistance to the advance, such value are said limiting velocity and the time constant is considered acquired after an equal time to 3 times, a value that indicates in how much time the speed has been reduced to 1/e of the value begins them.

 

43) Define a force centers them isotropa:

A force is centers them if it always turns out directed towards a fixed point said center, its module only depends therefore on the position of the point in motion regarding this center . The same force then is said isotropa in the case that the intensity of the force is independent from the direction that the carrier has respect to a system of nertial reference.

 

44) What is a tie onolomo:

A tie is a limitation to the freedom to move of a body, the tie is onolomo when it acts on the position while it is anolonomo when it acts on the speed of the body.

 

45) Describe the reaction force:

Draft of the characteristic of impenetrability of the solid ones that consists in a force that opposes to the force weight of the body preventing to the same one to catch up the center of the earth. Such force to second of the inclination of the plan can introduce 2 members, one orthogonal to the plan (normal reaction R_N ) and one parallel to the direct plan so as to opporsi to the motion (Force of friction).

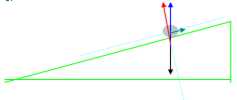
46) Describe the normal reaction:

Draft of the member second the normal school to the plan of the reaction force.

 

47) Describe the friction:

Draft of the member parallel to the plan of the reaction force. It is function of the atomic characteristics of the bodies to contact that comes expressed through following the 2 coefficients:

m_s = coefficient of static friction, it indicates that the body will begin to move single if will come impressa to the body a force R_To = R_N * m_s.

m_d = coefficient of dynamic friction, it indicates which force is necessary to continue to supply once that the body is in motion in order to maintain it in rectilinear motion uniforme R_A' = R_N * m_d is observed that m_d is < m_s .

 

48) As to define a thread:

It is an able inestendibile deformable system of esplicare a reaction to bind only dictates tension along its length.

 

49) Describe what ¨ and that motion describes a dampened oscillator:

Draft of a unidimensionale oscillator subordinate to one resistance of advance as an example of viscous type. the motion obtains from the the solutions is various to second of the coefficient of relative damping b to the viscous force.

if b = 0 žfree harmonic oscillating

if b is smallž dampened not periodic oscillating motion.

if b = b_critical ž is a motion dampened with return to the position of equilibrium in minor the possible time.

if b it is grande ž it is a motion dampened with return to the position of equilibrium without some oscillation.

 

50) Describe what ¨ and that motion describes a forced oscillator:

Draft of a unidimensionale oscillator subordinate to a resistance of advance as an example of viscous type to which moreover a variable force in the time in periodic way is applied. The motion obtains from the whose solutions are 2, one is equal to that one of the dampened oscillator and determines the transitory motion of the oscillator whose duration is function of b. 2ª the solution identifies the frequency of resonance in correspondence of which the oscillator oscillates with the greater energy also in relation to _{the critical} relationship b/b this second solution determines the motion of the oscillator to regimen.

 

51) What is the moment of a F force respect to a pole Or:

The force is orthogonal a carrier to a containing plan and indicating the ability that it has to carry out a spin, tasks that is to push a heavy one portone close to the axis, or more far away possible from the spin axis, it will be noticed that the provoked movement to force parity is greater in 2° the case. it assumes for the spins the same one meant that they assume the forces for the translations. It is as an example clearly that if the force is parallel to the carrier r that it combines it to the pole it is not in a position to esplicare some spin.

 

52) What is the axial moment of a force:

It is the projection of the carrier on an axis passing for the pole.

 

53) What is the angular moment respect to a pole Or:

It is orthogonal a carrier to the plan in which the indicating motion is carried out and the fact that m complete one spin regarding the pole. it assumes for the spins the same one meant that they assume the momentum for the translations. It is as an example clearly that if the speed of the point is parallel to the carrier r that it not combines it to the pole there is some spin.

 

54) Which it is the relation that alloy the moment of the force at the angular moment:

it is for the spins that that the is for the translations.

 

55) That what ¨ the impulse of a moment and how much is worth:

is that is equal to the variation of the moment of the momentum in 2 moments considers you.

 

56) Describe the motion of a point in a field of forces centers them:

The moment the motion is null therefore happens with constant angular moment and comes therefore described a flat motion with speed to areolare constant. In the case as an example that the force centers them it is the elastic force then the motion is generated from the composition of 2 harmonic motions and the turning out trajectory is in function of the phase relation one of the figures of Lissajous.

 

57) What is the elementary job of a force:

Draft of a largeness that turns out to be function of the trajectory. It is a largeness necessary to describe to the concept of energy in fact with one stupid example more is eaten and more a good job is made and ideally associating the food to the energy and the job to the job it follows that this last one is the esplicazione of the energy. Historically the 2 concepts are born for being able to compare performances of blot some.