Aeriform state
1) What is the meaning for aeriform:
The congloga aeriform term the gases and the vapors, the property of the aeriform ones are:
to) it does not possess any you form of it volume just because of the insufficient consequent forces of tie to the great energy kinetic , the aeriform one stretches therefore to occupy all the space to its disposition.
b) All the concoctions form to you from aeriform are homogenous, that is the physical property are equal in every point.
gas aeriform = that is found to of over of the critical temperature
aeriform vapor = that finds to one inferior temperature to the critical temperature.
2) What is the meaning for critical temperature and which of are the causes:
It is the temperature beyond which an aeriform one cannot be liquified, any is the pressure which he is subordinate.
It is due to the composition of the following forces:
a) forces of tie of Van der Waals that depend solo from the distance between molecules and therefore increases with P
b) la average speed of molecules decreases with decreasing of the temperature, until rendering liquid the aeriform one.
3) What is the meaning for normal conditions for a gas:
The physical conditions agree: temperature = 273,16 equal K to 0°C pressure = 1 atmosphere .
4) Thing expresses the Torr:
Mercury column is the pressure exercised from one (Hg) high 1 milimeter.
5) Thing expresses the atmosphere:
It is the medium pressure of the air at sea level
6.1) 1 Pa = 9,87 * 10-6 atm 6.2) 1 Torr = 133,3 Pa
6.3) 1 atm = 760 Torr 6.4) 1 dm3 = 1 liter
7) Characteristics of an ideal gas:
to) it is constituted from punctiform molecules whose volume is that is null.
b) the molecules do not exercise at a distance between of they some attractive or repulsiva force.
c) the molecules in hits between of they and with the container they are behaved like perfectly elastic spheres.
8) Enounce the law of Boyle for ideal gases:
For one given to ideal gas mass the volume it is inversely proporziona them to the pressure to constant temperature
![]()
The diagram that represents it is a branch of equilateral hyperbola
9) What is the absolute temperature:
It is the temperature not tied to the expansion of a particular substance but to the behavior of a whichever gas, the 0 of the Kelvin scale it represents in fact the temperature for which the volume of a perfect gas would have to be cancelled based on the following law of Charles.
10) Enounce the law of Charles for ideal gases:
For one given ideal gas mass, to constant pressure, the volume is directly proporziona them to the absolute temperature.
![]()
The diagram that represents it is one straight.
11) Enounce the law of Gay-Lussac for ideal gases:
For one given ideal gas mass, to constant volume, the pressure is directly proporziona them to the absolute temperature.
![]()
The diagram that represents it is one straight.
12) Enounce the equation of state of ideal gases:
It is one combination of the laws previously described
![]()
if reported to a single size it is worth P V = n R T
13) How much is worth R in the PV = nRT:
R is constant however can assume various values to second of the unit in which the pressure is expressed:
R = 0.0821 Atm * l * mol -1 * K-1
R = 8,31 kPa * l * mol -1 * K-1
R = 8,31 J * mol -1 * K-1
R = 1,99 cal * mol -1 * K-1
14) What is the compressibility factor:
It is ![]() the relationship can assume the
following values:
the relationship can assume the
following values:
< 1 in a real gas for low temperatures and pressures.
1 for ideal gases.
> 1 in a real gas for high temperatures and pressures.
15) Enounce the principle of Avogadro:
Equal various gas volumes, in the same conditions of temperature and pressure, contain the same one n° of molecules. The conglobato result is also it like the 3 previous laws in the PV = nRT
16) How much is worth the volume of one whichever gaseous substance to c.n.:
22,4 liters for every size of gaseous substance.
17) Differences between real gases and ideal gases:
to) molecules they are attracted between of they and therefore the volume is inferior regarding that one of the ideal gas. Therefore the P is sum of the pressure of the gas and one internal pressure.
b) the molecules have a not null volume therefore the real volume of the gas are given from the difference between the ideal volume and the covolume that is the volume occupied from molecules.
The model of the gas of van der Waals holds account of
these modifications ![]()
18) When real gases and ideal gases have similar behaviors:
To pressioni low in how much molecules they are distant between of they and therefore the insufficient attractive forces and to high temperatures.
19) What is the density:
It is the relationship between the mass of a gas and its volume, it is calculable from the PV = nRT, infatti d = gr/V
![]()
20) Which relation alloy the density of 2 gases in various conditions of pressure and temperature:
![]()
21) What is the relative density:
It is the relationship of the density of a gas regarding that one of an other, taken like reference, measuring both the density in the same conditions.
![]()
22) Describe the phenomenon of the gaseous dissosciation:
For some substances the relative density instead of being independent from the temperature diminishes to growing of the temperature, this has had to the fact that the temperature influences on their dissosciation.
23) What is the degree of dissosciation to :
It is the relationship between the n° of dissociated wharves and the n° of wharves it begins them. It varies between 0 and 1.
24) What is the theoretical density and the density experiences them and as they are tied:
dt = density of the substance not dissociated
ds = density of the substance dissociated with degree of dissosciation to
![]()
where n particle is the obtained particle number "that it is dissociated.
25) molecule Calculate n = n° that takes origin from the dissosciation of one in 3 reaction2SO " 2SO2 Or2 :
v = 3/2 = 1,5
26) What is the partial pressure:
It is the pressure exercised from a member of a gaseous mixture if alone it occupied the entire volume to disposition of the mixture, to the same temperature.
27) What is the fraction molar:
It is the relationship between n° of wharves of a member and the wharves totals of the mixture
28) Which relation never is not written but it is always present in the exercises on gas mixtures:
The sum of the fractions molars of the elements that constitute a mixture is equal to 1.
29) As the partial volume of a making gas is estimated part of one mixture:
Total occupied from the mixture for the fraction is multiplied the volume molar of the interested gas, from this value can be reached the n° of wharves of the gas through the PV = nRT.
30) Enounce the law of Dalton regarding the fraction molar and to the partial volume:
The law of Dalton establishes that every gas of a mixture acts independently from other present gases and the pressure total of the mixture is the sum of the pressures parziali. P = p1 p2 ... pn .
regarding the fraction molar:![]() regarding the partial pressure:
regarding the partial pressure:![]()
31) As the pressure of a gas collected on water is estimated:
It is equal to the difference between the external pressure and the vapor tension of the water for that date temperature. Moreover if there is an unevenness between the level of the water externally and inner to the binder, the hydrostatic pressure must be embezzled to the external pressure also.
32) As the hydrostatic pressure is estimated:
It is observed that 1 Torr is equal to the pressure exercised from column high Hg a mercury 1mm and whose density is 13,6 g/cm3. The proportion with the water is carried out whose density is 1gr/mm3 and it is obtained to how much Torr as an example corresponds an unevenness of the equal water to 1 cm.
33) Enounce the law of the combinations in volume of Gay Lussac:
When gaseous substances react or they are formed in a reaction, their volumes, measured in the same conditions of temperature and pressure, they are between of they in the relationship of entire and small numbers.
34) Aspects of the kinetic theory of gases:
The theory is developed to leave from following the 4 hypotheses:
to) the pressure it is due to the collisions of molecules with the walls of the container.
b) the collisions are elastic.
c) not is intermolecolari forces.
d) the medium kinetic energy is proporziona them to the absolute temperature.
Elaborating these hypotheses and on the base of cinematic considerations the equation of state of perfect gases is gained theoretically to which it was instead joints for via experiences them. An ulterior result also is that not existing a constant speed for particles of the gas, in how much the speed changes in continuation for via of hits, exists a speed that is that one possessed in a data moment from the greater particle number and dictates fashionable speed.
35) Define the phenomenon of the effusion:
It is the passage of a gas through a hole in conditions in which the phenomenon it is not influenced from hits between gas molecules.
36) Enounce the law of Graham on the speeds of gases:
The speeds to which different gases diffuse are inversely
proporziona them to the square roots of respect weights to you
molecolari.
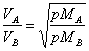
This law is a result of the kinetic theory of gases.
37) How much is worth molecular weight medium PM of one mixture of C62H 6 andCH6 :
It is the medium molecular weight that is estimated which summary of the products of the fractions molars for correspondent PM.
PM MIXTURE = cC6H6 * 6 PMCH6 cC2H6 * 2 PMCH6
38) That relation is between the number of wharves of one mixture and n° of wharves of its the members:
The n° of wharves of the mixture it is the sum of the n° of wharves of the members.
