Theorems on the limits
Limits of functions
1) Oneness of the limit:
Description: if 
e 
l1 = l2
if it were l1 ¹ l2 they would have to exist around of l1 and around of l2 between distinguished they to which 0 would have to correspond 2 intorni distinguished ofx thing that instead pu² not to happen inasmuch as the intersection of 2 intorni of x0 is still one around of x0 and will contain at least one point of x ¹ x0 in how much x0 is one point of accumulation (therefore every around of x0 0 contain at least one point of various dominion X fromx). After all therefore the intersection of 2 intorni is not empty against the made hypothesis.
2) Theorem of the permanence of the sign:
Description: if 
then f(x) > 0 definitively for x ® x0 where the term definitively
indicates that the property is valid for every x pertaining at least
one around of x0 with x ¹ x0 .
If 0 < l < ¥ then choosing and = l it is made so that around V of l it is (0, 2l) and for this around we will have one around of x0 in which the function is comprised between 0 and 2l.
Eye :
the fact that a function is > 0 does not imply that it it is
also its limit, as an example x2 is
definitively greater of 0 for x®0 (definitively excludes point x0 = 0 where x2 = 0)
but 
Improvement dim. : If 0 < l < ¥ then choosing and = l - m makes so that around V of l it is (m , 2l - m) and therefore can be extended the theorem saying that it is valid for every 0 < m. < l, that is a solo does not exist around but one for every m chosen between 0 exists some and l.
3) Relationship between the existence of an ended limit and the limitatezza of the function:
Description: If for a function exists a limit ended for x®x0 the function definitively is limited for x®x0
but is not said that if the function is limited then it admits an ended limit, as an example sgnx is a limited function but the limit for x 0 does not exist® .
4) Theorem of the comparison:
Description: If I have 2 having functions f(x) and h(x) the same limit l for x 0® x and one third function g(x) is definitively comprised between h(x) and f(x) for x ® x0 then also g(x) it stretches to the same limit l.
For every around V of l will have to exist around a U1 of x0 for which f(x) ? V and one around U2 of x0 for which h(x)?V, well for every x pertaining to the intersection of these 2 intorni it will be had that it is f(x) that h(x) they will belong to V and therefore also the g(x) that is between they comprised.
Esempio : calculation of the limit of sinx/x.
5) How much is worth the limit of the having product between f(x) having limitl 1 and g(x) limit l2 ?
Description: f(x)*g(x) has like limit l1* l2 .
Affinchè is true must be | f(x)*g(x) - l1* l2 | < and that it is obtained to leave from the expression f(x)g(x) with following:
1) 1 l 2 is writtenf(x)g(x)-l 1 l 2 =f(x)g(x)-l
2) one joins and it removes to 2° member l1* g(x).
3) Collecting it is reached shape f(x)*g(x) - l1* l2 = g(x)*(f(x) - l1 ) l1* (g(x) - l2 )
4) it is observed that both the terms between parenthesis for limit definition are smaller of and and that g(x) possessing un ended limit is a limited function therefore is |g(x)| < M for x ® x0 . The inequality is reduced therefore to the forma | f(x)*g(x) - l1* l2 | < Mand l1*and that given to the confirmation and arbitrariness the task.
6) How much is worth the having limit of function 1/g(x) limit l1 > 0?
Description: 1/g(x) has like limit 1/l1 .
Affinchè is true must be | 1/g(x) - 1/ l1 | < and that it is obtained to leave from | 1/g(x) - 1/ l1 | carrying out the minimum comun denominator who
gives back 
to the numerator of 2° the member
turns out smaller of and for
limit definition while to the denominator, in virtue of the theorem of
the permanence of the sign, we know that, having g(x) positive limit,
it is sure g(x) > m > 0 for x®x0 therefore we can
write 
in how much the denominator cannot be
cancelled and therefore through and we can render small how much we want the difference between
the limit and the function.
7) Under which conditions is possible to calculate the limit of one composed function?
Description: If 
and f(x) ¹ l definitively for x0®x
and
if 
then is had that 
It is demonstrated backwards asserting that a W of k exists around for which one around V of l i exist whose elements y are such that g(y) it is comprised in W. Is completed then an other step backwards in order to find one around of x0 composed from x such that f(x) has values on all V with the exception of l, such around finds which intersection between around U1 of x0 composed from x such that f(x) ? V and around U2 of x0 composed from all the x for which f(x) ¹ l.
8) Considerations on the limits of the functions monotone:
Description: a function monotonous admits always the limit and in particular it coincides with the Sup f(x) if the function is crescent and we consider around left of x0 , while he coincides with the Inf f(x) if the function is crescent and we consider a skillful one of x around0.
To demonstrate that if x are increasing then the limit is the Sup if we consider around left of x0 means to consider both the possible cases, that is defining Sup f: = l it is had:
to) l ? "
For definition of advanced end it is had:
* f(x) £ l comprised "x between -¥ and xor
* every For and > 0 exists xand a such one that f(x) and > l and therefore l is not more extreme advanced
Being the increasing function we will have evidently that " x comprised between xand and x0 are had that l-and < f(x) £ l that is l is the limit of f for x that stretches to x0.
b) l = ¥
The f in this case it is not limited advancedly therefore we will have to take like reference one value M of the function and to say that for the x to associated right ofthe x M to point M since the function is increasing it has that f(x) > M and therefore the limit is ¥ . If the null function had not been crescent we could have said.
Limits of successions to values in "
9) a convergent succession is limited.
Since a succession is not that a particular function, it follows that for it it is worth the theorem 29) according to which if for a function the function exists a limit ended forx®x 0 definitively is limited for x®x0 will be had therefore that for the n greater of a sure N, | ton | £ M0 that are behaved from advanced end while for the n comprised between 0 and N will have to exist a maximum M1 for | ton | in how much they represent a sottoset ended of ". After all therefore the succession ton is limited from the maximum between M0 and M1 .
10) a limited succession monotonous and is convergent.
11) Theorem bridge between the limits of functions and the limits of successions:
Description: 
> 
" succession ton to
values in X \ {x0}and convergent to
x0
Having to be worth 1° 0 the member then taken and > 0 will exist a d > such that for every x that it tos be distant from x0
0<|x - x0| < d it is had that | f(x)-l |< and and since the succession ton converges to x0 , then will exist a value such N that " n > N is had that | ton - x0 | < d and therefore will be had that | f(an) - l | < and for every n > N.
?
is proceeded denying 1° the member and obtaining that also 2° the
member is false, in particular the negation it asserts that $ and a such one that for every d > 0 x dexists ? X such that 0 < | xd - x0 | < d e | f(xd) - l | ³ and . To this
point it is made to stretch as an example progressively d to 0 dandogli
values 1, 1/2, 1/3..., 1/n and for every d is found
value xd for which | f(x) - l | ³ and . We have after all created a succession that
stretches to x0 but whose
image does not stretch to l all as
consequence of the absurd hypothesis begins them that 
.
12) Demonstrate that 
" a?", to > 1
Taking advantage of the theorem bridge we can
instead demonstrate that " succession bn ® ¥
has che 
. In fact:
the last term is reduced to 0 * to = 0 in virtue of 
the and therefore it is demonstrated that .
In order to demonstrate that is
necessary to bring back it to the 
shape that we
will demonstrate to be ugule to 0 for n ® ¥ , that is
obtained collecting like power 2to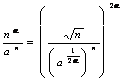 
. In order
to demonstrate finally that ® 0 per x ® ¥ is placed h = to - 1 and
disuguaglia through Bernoulli then from the theorem of the comparison
desume that ® 0 for x® ¥.
Just having used this inequality that it previews n ? ? it has forced to us to use [ bn ] 1.
13) Demonstrate that and is the Sup of succession 
the
naturally for n ® ¥ with n ? ? \ {0}.
It is necessary to demonstrate that the succession ton is convergent, that it happens for every limited succession monotonous and, we will demonstrate therefore that ton it is crescent and limited.
ton it is crescent is demonstrated verifying that the relationship ton / ton -1 is greater of 1 that is obtained bringing back the numerating to a shape of type (1 h)n and therefore disuguagliando through Bernoulli. The turned out obtained is valid for n ³ 2 in how much for n = 1 is only reached logical error 01 .
ton
is limited is
demonstrated analogous on a succession 
and
verifying that
relationship bn / bn -1 is smaller of 1 that is obtained
bringing back the numerator to one
forms of type (1 h)n and therefore disuguagliando through
Bernoulli.
It can therefore be asserted that ton it is comprised between 0 and bn which of the rest stretches to the
same limit in fact it has that if 
Giving a value to n an interval given from the assumed values is had givesn and from bn in which it is comprised and.
14) Demonstrate that it is also 
therefore not only for n ? ?\{0}
15) a limited succession to values in " has one convergent subsuccession .
2 cases can be verified:
a) an element to appears infinite times and therefore the subsuccession bn converges to to
b) the image of
the succession is an infinite entirety (in how much the succession
contains infinites various values) and limited
(in how much the succession is limited) therefore for the theorem
of Bolzano-Weierstass admits at least a
accumulation point l ? ". Every around of l a
subsuccession contains infinites values of the succession therefore
pu² to create that
stretches to l, in particular is the intorni 
that
for n® ¥ Un®l
the subsuccession is gained choosing " n?? which element of the succession ton re-enters in Un , in such a way creates a convergent subsuccession beginning from a succession that could is not it.
16) a fundamental succession is limited.
A succession is fundamental if " and > 0 a N exists ? ? such that taken 2 whichever greater elements n and m of N in the dominion ? of the succession it is had that | ton - tom | < and. In order to demonstrate that such succession is limited it is necessary to hold account that for the n comprised between 0 and N exists a maximum M0 for i assumed values give ton in how much they constitute a sottoset ended of "n. For n the ³ N instead it can be maggiorare |ton | through Cauchy-Schwarz in fact it is had
|ton| = | (ton - toN) toN | £ | (ton - toN) | | toN | therefore choosing m = N and arbitrarily placing and = 1 obtains that for every n ³ N it is had che |ton | £ 1 |toN| = M1 , after all therefore ton are limited from the maximum between M0 and M1 .
17) Criterion of Cauchy.
Description: a succession to real values is convergent > is fundamental
Demonstrate that a succession is fundamental means to demonstrate that " and > 0 a N exists ? ? such that taken to 2 whichever greater elements n and m of N in the dominion ? of the succession it is had that | ton - tom | < and. In order to make that one joins and it embezzles l to the inside of the module and disuguaglia through Cauchy-Schwarz obtaining itself that:
| ton - tom | £ | ton - l | | tom - l | < and in
fact from the convergence of the succession that is 
follows that given and > 0 will exist a N beyond which | ton - l | < and / 2
and replacing such result in the inequality obtained with
Cauchy-Schwarz the theorem turns out demonstrated.
? Occorre to take advantage of the 2 following theorems:
a) a fundamental succession is limited
b) a limited succession to values in " possesses always one subsuccession toknconvergent to l.
Dimostriamo the convergence of ton that is that | ton - l | £ and taking advantage of the fact that tokn converges to l, therefore we add and we embezzle tokn in the module and applying the triangular inequality, it is obtained
| ton - l | £ | ton - tokn | | tokn - l | £ and Il 2° member is smaller of and in every how much for n ³ N1 it will be had that
| toKn - l | < and / 2 while for definition of fundamental succession it is |ton - tom| < and / 2 for n, m ³ N2 and placing
m = kn is had that |ton - tokn | < and / 2 for n > N 2 .
With compact
44) K Is K "n then K is compact > is closed and limited
compact K implies that every succession to values in K has a subsuccession that stretches to x ? K therefore K is closed in how much contains its heads of accumulation. The limitatezza of K is demonstrated for absurdity asserting that if there were a succession not limited that it stretches to ¥, every its subsuccession would have ¥ limit and therefore is not true that every subsuccession stretches to one element x ? K and therefore we would not find ourselves on a compact .
? * limited K implies that every succession toK to values in K is limited
* Every limited succession possesses one convergent subsuccession to an element l? "n , such element l is stung of accumulation for K and therefore or is stung inner or is stung of frontier, and siccome closed K wants to say that it contains is the inner points that the frontier points, achieve some that K contain also l and after all we have tried that K is compact, that is that every succession to values in K has a subsuccession that stretches to l?K.