Theorems on the integrals
1) If f it is a limited function and D1 and D2 is 2 subdivisions of [ a,b ]
a) if D1 is finer than D2 has che s(D2,f) £ s(D1,f) £ S(D1,f) £ S(D2,f)
b) s(D1,f) £ S(D2,f)
to) In order demonstrating that s(D2,f) £ s(D1,f) we
suppose that D1 has only a
point z in more regarding D2 therefore will exist a k comprised between 1 and n such
one that the point z is comprised in the interval (xK-1 , xK) therefore does not make other that to write s(D2,f) as sum of 3 terms of which the
1° it is the inferior sum until to the point that precedes k, 2° the
term it is the product of the interval (xK-1 , xK) for the minimum on the same interval and 3° the term is
the inferior sum from k 1 until to n. That is 
is observed then that 2° the term
is sure £ of the term that
we would obtain which inferior sum on the sottosuddivisione (xK-1 , z, xK) in how much the more fine ones regarding (xthe K-1 , xK) and observing that the union of
this finer sottosuddivisione with 1° and 3° the term are not that
s(D1, f), than analogous demonstration it can be made for the advanced
sums and that in a generalized manner it is had 
,
it turns out demonstrated the part a) of the theorem.
b) it must be demonstrated that s(D1,f) £ S(D2,f), if the 2 confrontabili subdivisions are this always true (like are demonstrated in the part a) of the theorem), if instead the 2 subdivisions they are not confrontabili then can be taken one subdivision D3 : = D1 ? D2 that is finer than both and to assert based on the part a) of the theorem that
s(D1,f) £ s(D3,f) and also S(D3,f) £ S(D2, f) and since for every D subdivision it is had s(D, f) £ S(D, f) after all conglobando these 3 inequalities has s(D1,f) £ S(D2,f) and the theorem is demonstrated.
2) If f is one function limited in an interval [ a,b ]
f ? "(to, b) > " and $ one such Dsubdivision and of [ a,b ] that S(Dand ,f) - s(Dand ,f) < and
If f? "(a,b)
then 
and for definition of inf will be had that
taken and > 0 to a $ one D subdivisionandâ? such
that S(Dandâ? ,f) < and / 2
and one D subdivisionandâ
' such that s(Dandâ ' ,f) > - and / 2. After all taking one
D subdivisionand : =
Dandâ? ? Dandâ ' it will be had that
S(Dand ,f) - s(Dand ,f) £ S(Dandâ ',f) - s(Dandâ?,f) < I(f) and / 2 - I(f) - and / 2 = and .
? has the second integrabilità Riemann when the difference between the advanced end of the inferior sums and the inferior end of the advanced sums, stretches to 0, that it is obtained considering that such difference is comprised between 0 and difference S(Dand ,f) - s(Dand ,f) < and which can be rendered small a.voluntad operating on and.
3) If f it is a continuous function in the interval [ to, b] f ? "(a,b)
It is observed that a continuous function on a
limited interval is also uniform continuous on the same one therefore
for every and > 0 a d
can be found > 0 such that 2
taken aim whichever in the dominion whose mutual distance is smaller
of d , are had that their
images are found inferior at a distance to and / b-a. Enough therefore to choose one D
subdivisionand the whose
amplitude |Dand| he is smaller of d and it will be able to be found that the difference
between the Min and the Max on the single one spaces out is smaller of and / b-a and consequently
also the difference between the advanced sums and the inferior sums
will turn out smaller of and in fact 
and remembering that
if S(Dand ,f) - s(Dand ,f) < and then f ? "(a,b) it achieves some that the
theorem is demonstrated.
4) If f function monotonous in the interval is one [ to, b] f ? "(a,b)
The idea of the demonstration is to bring back to us to being able to assert that " and > 0 $ Dand , subdivision of [ a,b ]: S(Dand ,f) - s(Dand ,f) < and
Delivery therefore from 1° the member of this last one and I demonstrate that he is smaller of and :
in how much assuming the function monotonous increasing
it is had f(x) ³ Mthe e f(xi-1) £ mi
in how much |Dand| it is the amplitude of the greatest interval
of the subdivision.
in how much the image of a function monotonous crescent
is
limited from the 2 values assumed to the ends of the
interval.
Choosing therefore the D subdivisionand so that 
has S(Dand ,f) - s(Dand ,f) < and then f ? "(a,b).
5) If f it is a function limited in the interval [ to, b] and has a n° ended of points of discontinuità f ? "(a,b)
The idea of the demonstration is to bring back to us to being able to assert that " and > 0 $ Dand , subdivision of [ a,b ]: S(Dand ,f) - s(Dand ,f) < and
and therefore f? "(a,b). We suppose that the discontinuity point is to an end, as an example to and considering x?(a,b) it is had that in the interval [ x,b ] f ? "(x,b)that is " and > 0 $ is continuous f one D subdivisionandâ? such that is had
S(Dandâ? ,f) -
s(Dandâ? ,f) < and / 2.
In the interval [ a,x ] instead it is had 
in how much
for the thoroughness property if f it is limited then admits
inf and sup and supposes K = sup | f |.
having chosen such
point x that 
choosing therefore like subdivision Dand = Dandâ? ? {to} it is had:
S(Dand ,f) - s(Dand ,
f) = (M1 - m1)(x - a)
S(Dandâ? ,f) - s(Dandâ? , f) < 
and therefore the
theorem is demonstrated.
6) If f it is a function limited in the interval [ to, b] f is integrable according to Riemann > exists L? " for which "
d > 0 and >0 "such that " D subdivision whose amplitude is |D| < d it turns out |s(D,f) - L |< and .
7) If f and g they are integrabili functions tof bg is a integrable function in (a,b) and is worth:
Pu² to observe itself that
to) the advanced end of the function sum it is £ of the sum of the advanced ends of the single functions
b) the inferior end of the function sum is ³ of the sum of the inferior ends of the single functions.
c) Multiplying the inferior sums and the advanced sums for the same constant the integral that of is the difference cannot that be constant.
8) If f and g they are integrabili functions and f £g
It is necessary to demonstrate that the integral
of the function h(x): = g(x) - f(x) it is ³ 0, that it comes down from the fact that h(x) ³ 0 in how much g(x) ³f(x) therefore also the inferior end
of h is not negative and remembering the multiple inequality it is had that 
and the theorem is
demonstrated.
9) If f and one function integrable
a) f is integrable
b) f - he is integrable
c) |f| he is integrable
d)
is had that 
, in particular is had 
to) So that f he is integrable must be demonstrated that " and > 0 $ Dandsuch that S(Dand ,f ) - s(Dand ,f ) < and , in order to make that take advantage of the fact that f is integrable and therefore S(Dand ,f) - s(Dand ,f) < and . It is had:
where the obvious property of f has been
taken advantage of second which 
.
b) That f - he is integrable is demonstrated in analogous way to how much fact for f .
c) is demonstrated remembering that | f | = f f - and applying theorem 120) for the composition of integrabili functions.
d) 
infatti
f = f f -
where I have applied the triangular
inequality
in the last one I have used that f and f - they are positive functions and therefore also their integrals, and che | f | = f f - .
10) If f and one integrable function in (a,b) and c ? (a,b) then f he is integrable also on (a,c) and on (c,b) and turns out:
to) Demonstration that f? "(a,c) and f?"(c,b)
If f he is integrable on a D subdivision, then it is to greater reason on a D subdivisionand finer which it is joining to D point c. We will have therefore the following subdivisions: Dandâ? : = Dand ?(to, c) e Dandâ ' : = Dand ?(c,b)
the following equality varrà therefore:
but f is integrable along the subdivision
Dand therefore 
and will have therefore to be:
f ? "(a,c)
f ? "(c,b)
b) Demonstration that
in quanto
comes used 2 subdivisions finer than Dand . Of the rest it is had 
and therefore for the arbitrariness of and the theorem is demonstrated.
11) Theorem of the average:
Description: If f it is a integrable function in (a,b) and m is the inf while M are the sup always on (to, b)
moreover if f $ c for which are
continuous 
Remembering the inequality
e since for hypothesis of the theorem f he is integrable
therefore s(D, f) = S(D, f) is had that 
and
dividend for (b-a) the theorem is demonstrated.
In order to demonstrate 2ª the part enough to consider
that the image of a defined continuous function on an interval is
still an interval and therefore such $ c that .
12) If f it is a integrable function in (a,b) and continues in x0 ? (a,b) and c ? (a,b) then the integral function
is derivabile in x0 and turns out F' (x0) = f(x0).
Being f continuous in x0 are had that " and > 0 exist d > 0 such that |x-x0| < d e | f(x) - f(x0) | < and that is
f(x0) -and < f(x)
< f(x0) and demonstrated and having
that if f(x) > g(x) then 
, can be written:
to divide all for (x-x0) and ottenere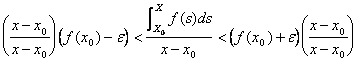 
In how much f(x0) and and f(x0) -and is constant.
Of the rest 
= 
in
fact it is had:
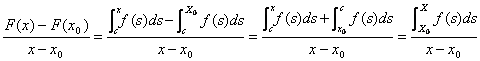
after all therefore 
ossia F' (x
0)= f(x 0is obtained).
13) fundamental Theorem of the integral calculus:
Description: If f it is a continuous function on [ to, b]
to) the integral function is derivabile on all [
a,b ] and its derivative is f(x) for every x ? [ a,b ].
b) If G
is one primitiva of f in [ to, b] 
to) It follows simply from the previous demonstration which observation that stavolta the f is not continuous in sol a point but in every point of [ a,b ] and therefore the integral function will be derivabile on all (a,b) and its derivative will be f.
b) taking to one point c inside to the segment [ a,b ]
can 
be scindere and siccome the primitive only
differ less than one constant this elide with - therefore it will be
also and the theorem therefore is demonstrated.
Integrals employee from a parameter
14) If f it is a continuous function in [ to,
b]x[c, d ] 
is
continuous on [ c,d ] and
a) 
therefore pu² to be only estimated the integral
of the limit
b) If f and fY is continuous on [ to,
b]x[c, d ] j ? There ([c, d]) and 
to) It is necessary to demonstrate that | f(y) - f(y0)| < and to
such aim replaces the definition of f for ognuna of the 2 maggiora with the module carried
under the sign of integral that is: 
and
remembering that the function f is continuous on a compact one has
that it is also uniform continuous therefore " and > 0 exists d > 0 such that for every
brace y, y0 ?[ c,d ] with |y-y0|<d it is had that 
That replaced
in previous the last integral gives back
if |y-y0| < d and quindi | f(y) - f(y0)| < and .
b) Leaving from the relationship the definition of this
last one increases themof the
function j (y) using is obtained: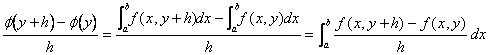 
Applying the theorem of the valor medium
is had that $q ?(0.1) for which 
the
and adding and embezzling fY(x,y) obtains 
. Having assumed fcontinuous Y and therefore also uniform it continues
inasmuch as it is defined on a compact one eliminates 
obtaining 
15) If f and fY is continuous in [ to, b]x[c, d ] and to and b they
are 2 having functions derived before continues in [ c, d] the function 
has derived continuous 1ª on [ c,d ] and
Integrabilità in improper sense
16-a) Criterion of the comparison
Is f,g: [ a,b)® " with b?"* , integrabili according to Riemann " w ? [ a,b), moreover sia 0 £ f(x) £ g(x) " x?[ x0, b) if g he is integrable in improper sense in [ to, b) f are integrable in improper sense.
f he is integrable in improper sense if it exists ended 
The 1° integral to second member it exists ended in how much the function is integrable according to Riemann " w ?[ a,b).
Of the 2° integral one deduces that being f positive, it
is an increasing function monotonous , therefore it admits limit and this
limit will be ended in how much if f £ g also 
and of the rest 
in how much g(x) is integrable in improper sense.
16-b) Criterion of the comparison
Is f,g: (a,b ]® " with to? "* , integrabili according to Riemann " w ? (a,b ], moreover sia 0 £ f(x) £ g(x) " x?(a,x0] if g he is integrable in improper sense in [ to, b) f is integrable in improper sense.
17-a) Interval not limited
It is f:[a, ¥)® "definitively positive for x® ¥ ed f? "[ to,w) for ogni w > a
a) if f it is infinitesimal of order to> 1 respect to 1/x for x® ¥ f is integrable in improper sense in [ a, ¥).
b) if f 1 respect to 1/x isinfinitesimal of order a£ for x® ¥ f is not integrable in improper sense in [ a, ¥).
17-b) Function not limited
It is f:[a, b)® " b?"definitively positive for x®b - ed f? "[ to,w) for ogni w ?(a,b)
a) if f it is infinite of order to< 1 respect to 1/(b-x) for x® b - f is integrable in improper sense in [ a,b).
b) if f 1 respect to 1/(b-x) forx b - ® is infinite oforder to ³ f is not integrable in improper sense in [ a,b).
18) If f it is defined on an interval and | f | he is integrable in improper sense in the f is integrable in improper
sense and 
In order to demonstrate that f he is integrable in improper sense enough to apply the theorem of the comparison using |f| in order to establish that also f and f - they are integrabili in improper sense and therefore also f being f = f - f - .
For the formula instead it is had: 
Where it has been used:
to) f = f - f - .
b) the triangular inequality.
c) f and f- they are positive functions, therefore also their integrals, and therefore the modules are useless.
d) | f | = f f - .