Theorems on the functions of 2 variable ones
Functions of 2 variable ones
1) If f he is differentiable in x?X with opened (that is if it exists to ? "n such that f(x h) = f(x) <a, h > o(||h||) for h®0)
a) f is continuous in x
b) exists the partial derivatives of f in x and it can be written: f(x h) = f(x) <`f(x), h > o(||h||) for h®0
c) exists the directional derivatives Dvf(x) for every payer and is worth the formula Dvf(x) = <`f(x), v >
to) From the differenziabilità definition inserting the modules it is drawn |f(x h) - f(x)| = |< a,h > o(||h||)| for h®0. Applying to the inequality of Cauchy-Schwarz (that is |< a,h >| £ ||to|| * ||b|| ) to 2° the member it is obtained |< a,h > o(||h||)| £ ||to||*||h|| ® 0 for h®0, therefore f is continuous being |f(x h) - f(x)| < and.
b) In the differenziabilità definition K toh is replaced t*e and t*e K and K are obtainedthat(f(x)-f(x))/t = <,> taking advantage of the made that ||andK|| = 1 being the canonical base constituted from payers therefore the derivative in the direction xK of the base canonical is equal to the member k-esimo of to and therefore it can be placed to = `f(x).
c) In the differenziabilità definition is replaced t*v to h and are obtained that (f(x t*v)-f(x))/t = < to, v > taking advantage of the fact that ||v|| = 1 being v a payer. Therefore the directional derivative along one whichever direction v is equal to the produced to climb between the gradient of f(x) and carrier v.
2) f is one derivabile function in x?X opened
f(x h) = f(x) <`f(x), h > o(||h||) for h®0 > f he is differentiable in x
the derivabilità of f in x concurs to replace `f(x) in f(x h) = f(x) < a,h > o(||h||) for h®0 and we find again the definition of differenziabilità in x.
? The differenziabilità implies the validity of f(x h) = f(x) <`f(x), h > o(||h||) like described from the 101-b)
3) Theorem of the valor medium for more variable functions:
Description: If f it is a continuous function on a segment [ x,y ] X then:
a) If v = (y-x)/ ||y-x|| he is a payer of this segment and exists the directional derivative along v for every point pertaining to the segmento exists q0 comprised between 0 and 1 such one that
f(y) - f(x) = Dv f((1-q0)x q0y) * || y-x ||.
b) If moreover f he is differentiable in every point of the segment exists a q0 such that
f(y) - f(x) = < `f((1-q0)x q0y), y-x >.
to) filler to apply the theorem to Us of the valor medium along direction v through the function jv(t): = f(x tv) quale the concur of dealing one function of 2 variable like one function of one variable. of it it is observed that:
jâ(t0) = Dv f(x t0v) , j(0) = f(x) , j(||y-x||) = f(y)
therefore applying the theorem of valor the medium unidimensionale finds that it exists t0 for which
f(y) - f(x) = j(||y-x||) - j(0) = jv' (t0) * ||y-x|| = Dv f(x t0v) * ||y-x||
and placing q0 = t0 / || y-x || obtains the enunciated one of the theorem.
b) From the part to of the theorem we know che f(y) - f(x) = Dv f((1-q0)x q0y) * || y-x || while from the differenziabilità it achieves that it is worth the formula Dvf(x) = < `f(x), v >, replacing it is had che:
f(y) - f(x) = < `f((1-q0)x q0y), v > * || y-x ||
and being v = (y-x)/ ||y-x|| of it it achieves the theorem.
4) Theorem of differentiates them total:
Description: If a U of x exists around in which f is derivabile(exist all the partial derivatives in x) and if the partial derived is continuous in the point x f he is differentiable in x.
We must try that f(x) he is differentiable , that is
that and f(x h) = f(x) <`f(x), h > o(||h||) for h®0 or analogous the function 0
extended 
can® be demonstrated that or for
® 0
To such aim the first 2 terms of the numerator and through the medium theorem of valor for the more variable functions are taken long junior clerk the directions of the payers of the canonical base, us filler to having fx1 and fx2 from being able to collect.
f(x1 h1 , x2 h2) - f(x1 , x2) = [ f(x1 h1 , x2 h2) - f(x1 , x2 h2) ] [ f(x1 , x2 h2) - f(x1 , x2) ]
and applying the theorem of the valor medium along and1 and and2 to the terms contained in ciascuna of the 2 quadrants, one obtains that:
f(x1 h1 , x2 h2) - f(x1 , x2) = fx1(x1 q1h1 , x2 h2)h1 fx2(x1 q1h1 , x2 h2)h1
which replaced in the definition of Q and collecting h1 and h2 gives back:
and being the terms 
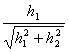and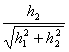 
both greater of 1 and for hypothesis of the theorem
continuous both the partial derivatives then will not have that when h®0, Q(h1,h2)®0 and
therefore the theorem is demonstrated.
5) If f he is 2 times differentiable in x?X with opened fX nX m (x) = fX MX n (x) "m, n = 1..., n
6) If f he is m times differentiable in x?X with open and dx it is such that segment [ x dx ] X then
a)
Vige the formula of Taylor with the rest of Peano 
for dx®0
e 
is
the only one polynomial of degree £ m that the verification.
b) If moreover f he is m 1 times differentiable in (x dx) then exists q0 such that:
to) In short it must be verified that 
or equivalent that 
.
Remembering that the polynomial of Taylor it
is such that fK(x0) = TnK(x0) follows that h(x0) = 0 and the theorem of the valor can be applied medium:
h(x dx)=h(x dx)-h(x) = Dvh(c)||dx|| = <`f(c),
dx > = 
and remembering the triangular inequality 
it is had
|h(x dx)| = 
must therefore be only
demonstrated that 
that it obtains for induction
from the same theorem, in fact it is had:
p0 ® the theorem is true for m=1 in how much finds again the differenziabilità definition
p1 ® supposes the valid theorem until to m-1, therefore applying it to hxi it is had:
hxi (x dx) = hxi (x) 
for dx ® 0
in fact hthe xi are m-1 differenziabili times and have the derivatives of null order £ m in x0 , are had therefore
hxi(x dx) = o(||dx||m-1) hxi(x qdx) = o(||qdx||m-1).
Replacing this result in [ 1] the theorem is demonstrated, in fact it is had:
h(x dx) =
£ 
= 
The oneness of the polynomial of Taylor is demonstrated considering P(x dx) of degree such £ m that
f(x dx) = P(x dx) o(||dx||m) for dx®0, of the rest it is also f(x dx) = Tm(x dx) o(||dx||m), uguagliando it is had:
P(x dx) - Tm(x dx) = o(||dx||m and since both i polinomi are of degree £ m it achieves some that o(||dx||m it is not in a position to absorbing no term of same and therefore P(x dx) = Tm(x dx).
b) the formula of Taylor with the rest of Lagrange is demonstrated in equivalent way bringing back itself to the case unidimensionale where to be able to apply the already famous formula, in particular the (t) is used jv = f(x tv) to which the rest of unidimensionale Lagrange is applicable, for its derivatives it is had:
jvk (t) = Dkvv... v f(x tv) if 0 < t < ||dx|| jvm 1 (t) = Dm 1vv... v f(x tv) if 0 < t < ||dx||
applying therefore the theorem of unidimensionale Lagrange:
jv(||dx||) = jv(0) 
and since it differentiates them df(x) introduces in the shape dKf(x) = f K(x) (dx)K and replacing the theorem it is demonstrated.
7) If f convex on with To convex and opened function is one
a) f is continuous in To and admits derived partial left rights and in To.
b) if f he is derivabile in one point x?To f he is also differentiable in x.
8) If f differentiable function in x isone?To with convex and opened
a) if f it is convex f(x) ³ f(x0) <`f(x0), x-x0> every for x?To
b) if f it is closely convex f(x) > f(x0) <`f(x0), x-x0> every for x?To, x ¹ x0 .
The result obtained for the convex functions in one variable f(x) ³ f(x 0 ) f â(x 0)(x-x0)throughthe function is applied
jv(t) = f(x tv) being jv(0) = f(x0), jv(||x-x0||) = f(x) and jv'(x0) = demonstratedDv f(x) and having that for
a differentiable function D vis hadf(x) = < `f(x), v > choosing t = || x - x0 || , 
and replacing, the
theorem is demonstrated.
9) If f differentiable function in every point x is one of with To, convex and opened
a) f is convex > f(x) ³ f(x0) <`f(x0), x-x0> every for x0?To.
b) f is closely convex > f(x) > f(x0) <`f(x0), x-x0> every for x0?To.
10) If f differentiable function is one 2 times in every point x of with To, convex and opened
a) f is convex in A > d2f(x) = < Hf (x)dx, dx> ³ 0 for every dx ? "n .
b) f is closely convex in To if for every x?To is had < Hf (x)dx, dx> > 0 for every dx? "n and dx ¹0.
Using the formula of Taylor with the rest of Lagrange 
replacing for m = 1si it has that a q
exists ? (0.1) such that 
that ³ 0 in 
how much can also write being the
convex function is had that f(x) ³ f(x0) <`f(x0), x-x0>.
11) If f differentiable function is one 2 times in every point x of with To, convex and opened
a) f is convex in A > Hf (x) is semidefined positive every for x ? To.
b) f is closely convex in A > Hf (x) is defined positive every for x ? To.
12) If f he is differentiable in x?To opened and x it is stung of local end for f x is one critical point that is `f(x) = 0
places but attention to the fact that a critical point is not necessarily a local end, or if f is not differentiable in x0 , x0 can be end point or not.
13) If f it is with convex and x are one critical point of f then:
a) If one around of x exist in which f it is convex x is stung of minimum of f.
b) If one around of x exist in which f it is concava x is stung of maximum of f.
Moreover if f he is 2 times differentiable in x then:
c) If Hf (x) is defined positive x is one point of minimum strongly of f.
d) If Hf (x) is defined negative x is one point of maximum strongly of f.
and) If Hf (x) is not semidefined positive semidefined some negative x is one saddleback point of f.
f) If Hf (x) is semidefined positive o semidefined negative x is of saddleback or maximum or minimum for f.
to) f differentiable and convex it implies that the function is all over to the tangent plan in x and therefore these cannot that to be a minimum point.
b) f differentiable and concave it implies that the function is all under to the tangent plan in x and therefore these cannot that to be a maximum point.
c) pu² to apply to the theorem of Peano 
holding account that the critical point in x implies that
the gradient is null and therefore also it differentiates them, df(x)
= <`f(x), dx > = 0, the
formula becomes 
and considering that if the
Hessiana matrix is defined positive then the smaller autovalore is
positive it can minorare f(x) and to say 
and
therefore for dx®0 that is
in around a much small of x is had that the function assumes greater
values that not in x that therefore it is one point of minimum.
d) it is demonstrated to point c analogous).
and) In every around of x it is had that Hf is semidefined positive for some carriers and semidefined negative for other carriers that is in order better to say of is not semidefined positive semidefined some negative therefore is values for which differentiates them is positive and values for which it differentiates them are negative and therefore points in which the function it is greater that not in x and points in which the function she is minor who in x therefore x are not one saddleback point.
f) it is demonstrated with a practical example, that is 3 functions (x are taken14 x24 ), (x14 - x24 ) and - (x14 x24 ) having all and three the same hessiana matrix constituted from all 0 and same critical point (0,0) and are demonstrated that for the 1ª it is a minimum point, for the 2ª are a point of saddleback while for the 3ª it is a minimum point.