Theorems on the differential calculus them and the approximation of functions
Differential calculus them
1) If f he is derivabile in x0 pertaining to an interval f is continuous in x0 .
For to be continuous the function it must be had that 
and since if f he is derivabile in x0 then must be ended the 
limit that is the f(x) is approssimabile in x0 from one straight tangent of equation
y = f(x0) f ' (x0)*(x-x0) said of better linear approximation in particular f(x) and the straight one to be distant between of they o(x-x0).
One obtains therefore that
that is f it
is continuous in x0 .
1-a) the derivative of the product of a function for one constant is equal to the constant multiplied for the derivative of the f.
1-b) the derivative of the sum (difference) of 2 functions is equal to the sum (difference) of the derivatives of the 2 functions.
1-c) Derived of the product of 2 derivabili functions:
Description: 
In the definition of derivative
applied to the function (fg) ' sum and embezzles to the numerator f(x0)g(x) and scinde therefore the
relationship in the 2 relationships increases them f â(x0) and gâ(x0) multiplies to you respective for g(x) and f(x0). It is only the continuity in x0 that concurs us to replace g(x)
with g(x0).
2) Derivative of the relationship of 2 derivabili functions:
Description: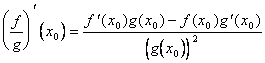 
The definition of derivative is used before applied to the function (1/g) and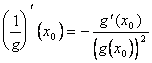 
is
obtained after which the 65-c is applied) to the 1/g and f.
3) Formula of Leibnitz for the calculation of the derivative n-esima of the product of 2 derivabili functions:
Description: 
In practical the coefficients they are those of the triangle of Tartaglia and 1° the index of the derivative comes down while 2° the index knows them.
4) If g he is derivabile in x0 and f he is derivabile in g(x0) then the composed function is derivabile in g(x0):
Description: 
The customary extensive version of the derivative is
written is for g: 
That for f°g: 
and replacing the 1ª in 2ª the theorem it turns out demonstrated.
5) If a function f continues and closely monotonous on an interval (therefore invertible and the inverse one is continuous in its dominio) and if this is derivabile in x0 and various from 0, the inverse one is derivabile in f(x0).
Description: 
The definition of derivative is applied
in which the correspondents x in fact f can
themselves be replaced-1(y)®x, f -1(y0)®x0 , y0 ®f (x0) and y®f (x) and the theorem turns out
demonstrated.
6) (x to) ' = tox to -1
It is demonstrated with the coincided definition
of derivative that is 
con h = x0 - x.
In particular in it it is necessary to replace f(x h) with (x h)to and f(x) with xto it is made in way to collect to outside x to -1 and then on remaining inner to the parenthesis the remarkable limit (1 x) to =1 to x is used o(x).
7) (andx) ' = andx
It is demonstrated with the coincided definition
of derivative that is con h = x0 - x.
In particular in it it is necessary to replace f(x h) with and x h and f(x) with andx to collect itself to outside andx and then on remaining inner to the parenthesis one uses the remarkable limit (andx - 1)/x ® 1 for x ®0.
8) (sinhx) ' = coshx
Remembering that sinhx = (andx - and - x)/2 to derive it it is reduced to observe that the constant can be capacity outside while the derivative of the difference is equal to the difference of the derivatives, of which the derivative of and- x are estimated like derivative of a function composed to the function not derived for the derivative of the argument, replacing finds the definition of coshx.
9) (coshx) ' = sinhx
Remembering that coshx = (andx and - x)/2 it is demonstrated in way of all the analogous one to how much fact for sinhx.
10) (logto|x|) ' = (logtoe)/x
It is demonstrated with the coincided definition
of derivative that is con h = x0 - x.
In particular in it it is necessary to replace f(x h) with logto|x h| and f(x) with logto|x| to collect itself to the outside 1/x so as to to bring back itself to the logarithm that multiplies the definition of and like limit of one succession
11) (tox) ' = tox log to
Remembering that 
it is applied
to this last one the rule of derivation for the composed functions and
on the result it is considered just log a like one constant.
12-a) (sinx) ' = cosx
It is demonstrated with the coincided definition
of derivative that is con h = x0 - x.
In particular in it it is necessary to replace f(x h) with sin(x h) and f(x) with sinx and then the formula for the breast of one is used sum ossia sen(to b) = sentocosb costosenb and finally the remarkable limit senx/x ®1 for x®0.
12*-b) (cosx) ' = - sinx
It is demonstrated with the coincided definition
of derivative that is con h = x0 - x.
In particular in it it is necessary to replace f(x h) with cos(x h) and f(x) with cosx and then the formula for the cosine of one is used sum ossia cos(to b) = costocosb - sentosenb.
13) (tgx) ' = 1 tg2x = 1/ cos2x
It is demonstrated remembering that tgx = senx/cosx and using the rule for the derivative of the relationship of 2 derivabili functions.
14-a) (arcsinx) ' = 
It is necessary to apply the theorem for the derivation of the inverse function. To such need we observe that
a) arcsinx is the inverse one of senx which is a closely increasing function in [ -p/2, p] and having like derivata /2 the function cosx that in the interval (-p/2,p/2) are always ¹ 0 therefore will not have never that the inverse one has one tangent vertical and therefore are always derivabile.
14-b) is placed y =
arcsinx and using the theorem
is had therefore 
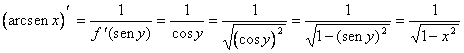
where in the last passage it has been taken advantage of that if y = arcsinx then is also true that x = seny.
15-a) (arccosx) ' = 
It is demonstrated in analogous way to how much fact for arcsinx.
16) (arctgx) ' = 
It is necessary to apply the theorem for the derivation of the inverse function. To such need we observe that
a) arctgx is the inverse one of tgx which is a closely increasing function in [ -p/2, p] and having like derivata /2 2 function1 tgx ³ 1 in the interval (-p/2,p/2) are therefore always ¹ 0 therefore will not have never that the inverse one has one tangent vertical and therefore are always derivabile.
b) is placed y = arctgx
and using the theorem it is obtained:
where in the last passage it has been taken advantage of that if y = arctgx then is also true that x = tgy.
17) (|x|) ' = sgnx
It is demonstrated with the coincided definition
of derivative that is con h = x0 - x.
In particular in it it is necessary to replace f(x h) with |x h| and f(x) with |x| dopochè inasmuch as h®0 is supposed negligible and melting the modules are obtained to 2 various fractions, that one for x > 1 have like limit 1 while that one for x < 1 has like limit -1 that it coincides with the definition of the function sgnx.
18) If f he is derivabile in x0 ? (a,b) and f f ' (x has a local end in x 00) = 0
We demonstrate the case in which x0 are one point of local maximum.
One around of x will have to exist0 in which f(x) < f(x0) that is f(x) - f(x0) < 0 comprised per x between (x0 - and) and (x0 and).
The relationship increases will have 
them
therefore the smaller numerator of 0 therefore:
* if we find
ourselves to the left of x0 the
denominator is negative therefore 
and therefore
also the limit that is the left derivative in x0.
* if we find
ourselves to right of x0 the
denominator is positive therefore 
and therefore
also the limit that is the skillful derivative
in x0.
For the derivabilità of f in x0 must be the limit from equal right to the left limit from, condition that only is respected if f' (x0) = 0.
19) Theorem of Rolle:
Description: If f it is continuous in [ a,b ] and derivabile in (a,b) and if f(a) = f(b) exists one such point c that f â(c) = 0.
Being f a continuous function on a compact one then it admits Min and Max and therefore can be verified:
to) if the function is constant f(a) = f(b) = f(c) = Min = Max therefore f â(c) = 0 for every c ? (a,b).
b) If Max > f(a) then must exist a point of end c in which the 81 at least) says that f â(c) = 0 to us, analogous if Min < f(a).
20) Theorem of Cauchy:
Description: If f and g they are continuous functions in [ a,b ] and derivabili in (to, b) exists one point c ? (a,b) such that
(f(b)-f(a))gâ(c) = (g(b)-g(a))f â(c).
I lead back myself to being able to apply to the theorem of Rolle defining on [ a,b ] one function h: = (f(b) - f(a))g(x) - (g(b) - g(a))f (x) such that h(a) = h(b) will have therefore to exist a point of estrem c in which h' (c) = 0. Imposing that the derivative 1ª of h(x) (considerino (f(b) - f(a)) and (g(b) - g(a)) as constant) is equal to 0 obtains the formula of Cauchy.
21) Theorem of the valor medium:
Description: If f it is continuous in [ a,b ] and
derivabile in (to, b) exists one such point c that 
It is demonstrated placing g(x) = x in the theorem of Cauchy.
22) If f it is continuous in [ a,b ], derivabile in (a,b)
and if 
exists 
For the theorem of the valor medium one such
point c exists that , making the limit for c ® to obtains the result.
23) If f he is derivabile in (a,b) f ' does not admit discontinuity of 1ª species (of jump)
The theorem 22) says to us that if had to then exist the 2 limits from right and left in point x0 these would be equal to f ' (x0) and a f '-(x0) but the derivabilità imply that f ' (x0) = f '-(x0) therefore us cannot be jump discontinuity, are instead possible discontinuities of 2ª species.
24) If F and G are primitive functions in an interval of the same one f exists one constant C ? " such that
G(x) = F(x) C " x?I
It comes defined an equal function g(x) to the difference between G(x) and F(x), its derivative before is the difference of the derivatives first of G(x) and F(x) which but coincide with f of which F and G they are primitive for hypothesis of the theorem, therefore g' (x) = 0.
Applying the theorem of the valor medium 
and therefore g(x 2)= g(x 1is obtained) and for the arbitrariness of x1 and x2 follows that g he is constant therefore the 2 primitive F
and G is equal less than one constant.
25) If a defined function f on an interval has a discontinuity of 1ª species f does not admit primitive.
If for absurdity one primitiva, its derivative had to exist, that is f it would have a discontinuity of 1ª species that it is impossible as demonstrated to the point 86) where it asserted that if a function f is derivabile then its derivative 1ª cannot admit discontinuity of 1ª species or jump.
26) If f he is derivabile in an interval and f â?
it is in limited it that is exists a such L that | f ' (x) | £ L f is lipschitziana in the
interval with constant of Lipschitz L that is 
.
I can choose x arbitrarily and y and to find for the theorem of valor medium an inner point to they that the same derivative of the straight one has that it combines x and y and siccome this derivative must be £ L follows that this will be true " x, y.
and therefore the function is lipschitziana.
27) If a function is derivabile in (a,b)
a) f â(x) ³ 0 " x?(to, b) > f is crescent in (a,b)
b) f â(x) £ 0 " x?(to, b) > f is decreasing in (a,b)
c) f â(x) > 0 " x?(to, b) f is closely increasing in (a,b)
d) f â(x) < 0 " x?(to, b) f is closely decreasing in (a,b)
I demonstrate alone the case a) in how much the other demonstrations are analogous.
Assuming that 1 < x isto < x2 < b, applying the theorem of the valor medium, will exist one point c in which
f(x2) - f(x1) = f â(c)(x2 - x1) ³ 0 in how much f â(x) ³ 0 for hypothesis of the theorem while (x2 - x1) ³ 0 in how much x1 precede x2 for our hypothesis therefore f(x2) ³ f(x1) " x1 , x2 from which follow that the function is crescent.
? If f the relationship is increasing then increases them also cannot that be 0 ³ and therefore the derivative 1ª that of it is the limit for x ® x0 .
28) Theorem of de the Hopital:
Description: If f and g they are 2 derivabili functions in (a,b) and satisfy the 3 following hypotheses:
a) 
b) g' (x) ¹ 0 for ogni x?(a,b)
c)
then is had that also 
.
from the c) derives that you it must around be 
a , of the rest this is equivalent to 
the for the theorem of Cauchy in fact if f and g they
are continuous functions in [ a,b ] and derivabili in (to, b) then,
taken 2 points x,y in a around skillful one of to, exist one point c ? (a,b) such that 
. Al to stretch y®to , for the
hypothesis a) has that 
that is 
that it demonstrates the theorem.
Polynomial approximation
29-a) Formula of Taylor:
Description: 
To the aim to carry out an approximation of the f(x) for x®x0 the following observations are extrapolated:
to) If f(x) it is continua f(x) = f(x0) o(1) = T0(x0)
b) If f(x) 0)(x - x 0) o(x - x are derivabile f(x)= f(x 0) f ' (x0) = T1(x0)
In a generalized manner therefore the
approximation is come true imposing the contact of order n between the
function and the polynomial , in particular T n (k)(xmust be had0) = f (k) (x0).
Intuitivamente deduces that the polynomial of Taylor of order n
it must assume the shape Tn(x)
= to0 to1(x-x0) to2(x-x0)2 ... ton(x-x0)n in which the value of the term tox can be gained imposing that Tn (k)(x0) = f (k) (x0) > k!an = f (k) (x0) and therefore ton = (f (k) (x0))/(k!) and
the polynomial will be able therefore after all to be written 
29-b) Formula of Mac Laurin
Description: 
is not
other that the formula of Taylor with x0 = 0.
30) Theorem of Peano
Description: If f 0 the
polynomial of Taylor ofdegree n
are n times derivabile in x the only one
polynomial of such £ degree is
n that:
a) f(x) = Tn(x) o((x-x0)n) for x®x0
b) Tn(k)(x0) = f (k)(x0)
b) it derives from the considerations carried out in the construction of the polynomial .
to) That Tn(x) is a polynomial with these characteristics is gained for induction in fact:
* true E' for T0(x) = f(x0) o(1)
* true E' for T1(x) = f(x0) f â(x0)(x-x0) o(x-x0)
** Supponiamo that it is true for every derivabile function n-1 times and has f(x) = Tn - 1(x) o((x-x0) n - 1)
therefore applying de the
Hopital is had that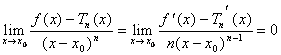 
Where nell' last passage
sfrutta ** observing itself that 
it is polynomial
of Taylor of degree n the -1
of 
.
The oneness of the polynomial of Taylor is demonstrated considering P(x dx) of such £ degree n that f(x) = P(x) o((x-x0) n ) for x®x0 , of the rest is also f(x) = Tm(x) o((x-x0)n), uguagliando it has: P(x) - Tn (x) = o((x-x0) n ) and since both the polinomi are of degree £ n achieves some that o((x-x0) n ) is not in a position to absorbing no same term of and therefore the P(x) = Tn(x).
31) If f he is derivabile in x0?(a,b) at least n ³ 2 times and if all the derivatives of inferior order to n are null in x0 then
n is pari > x0 is one point of local minimum strongly if the derivative ennesima of f in x0 is > 0
x0 is one point of local maximum strongly if the derivative ennesima of f in x0 is < 0
n is dispari x0 is not one point of end
From the theorem of Peano, considering that all the derivatives of smaller order of n are null in x0 it follows that
for x ® x0
if n ³ 0 is equal(x-x 0 ) and therefore if f (n)(x0) > 0 then is a minimum in x0 in how much in its around f(x) > f(x0)
while if f (n)(x0) < 0 then is a maximum in x0 in how much in its around f(x0) > f(x)
if n the sign of f(x)-f(x the 0 is uneven) it depends is from the sign of the derivative that they give the position in which the x are found considered respect to x0 , in particular will be able to be noticed that if as an example on the left f(x) > f(x0) well to right contrary therefore x is had0 is not a local end.
Convex functions
32) a function is closely convex in (a,b) > " to < x1 < x2 < x3 < b has the following relation of order:
P(x1,x2) £ P(x1,x3) £ P(x2,x3) being P the combining slope of the 2 points.
33) If I have one convex function
a) " x?(a,b) they exist ended the limit of the derivatives first from right and left
b) " x?(a,b) the limit of the derivative before from right is greater of the limit of the derivative before from left
c) the derivative before from right and the derivative before from left are crescents in (a,b)
d) f is a continuous function in (a,b)
to) the existence of the limit ended for left the skillful derivatives and in every pertaining point to (a,b) it is demonstrated simply taking 5 points of which that one they centers is x0 , the 2° it is x that stretches to x0 from left and the 4° it is y that it stretches to x0 from right well making to stretch x to x0,the limit of the slope of combining corresponds to the derivative before from left in x0 and is limited advancedly (for 95) from the slope of the straight one that joins x0 with 5° the point, therefore this limit exists ended in how much for a function monotonous the limit always exists, it is ¥ if the function is not limited while if the function is limited, I exist ended the limit. Analogous making to stretch y to x0 the limit of the slope of combining corresponds to the derivative before from right in x0 and is limited inferiorly (for the 95) from the slope of the straight one that joins x0 with 1° the point.
b) the derivative from right in x0 is greater of the derivative from left in how much every point to right of x0 has inferior slope respect to every point to the left of x0 carrying out the limit of the slopes the theorem is demonstrated.
c) is demonstrated that f ' are crescent remembering that f ' are not other that the limit for h®0 of P(x, x h), therefore considering x1 < x2 must be demonstrated that f ' (x1) < f ' (x2) that is P(x1 , x1 h) < P(x2 , xthe 2 h) that it happens based on the 95) and designing a convex function and on the abscissas points to, x1 , x1 h, x2 , x2 h, b have two disuguaglianze P(x1 , x1 h) < P(x1 , x2 h) and P(x1 , x1 h) < P(x1 , x2 h) therefore P(x 1 is hadalso , x1 h) < P(x2 , x2 h). Al to stretch h®0 the theorem is demonstrated.
d) the existence of the limit for the derivative before is from right that they give left implies the continuity is from right that they give left in fact if a function is derivabile in a point is also continuous in that point.
34) f it is convex in (a,b) > exist ended the derivatives from right and left in every point and are increasing functions.
35-a) If f he is derivabile in (a,b) the following affirmations are equivalents:
a) f is () closely convex in (a,b)
b) f â? it is closely increasing in (a,b)
c) " x0?(a,b) the function is found to of over of the straight tangent of better linear approximation in x0
to) and b) if of it it demonstrates equivalence directly observing that derivabile it means f â? = f â?- = f â? and then applying 97).
c) if of it it demonstrates equivalence to a) remembering that nel 96) we had established that the slope respect to x0 is greater for the points to right of x0 that not for the points to left of x0 that ³ f â(x 0)(x-x 0 canbe reassumednella formula f(x) -f(x0)) that ³ f(x 0 ) canalsobe written f(x) f â(x0)(x-x0) where 2° the member is the straight one of better linear approximation in x0 .
35-b) If f he is 2 times derivabile in (a,b) then
a) f is convex in (a,b) > f '' ³ 0 in (a,b)
b) f '' > 0 f is closely convex in (a,b)
The f convex we have seen in the 98-a) implies that the derivative before is closely increasing therefore being the second derivative correspondent to the derivative before f â? it is ³ 0 in how much derivative of one increasing function.
36) If f it has one flexed in x0 ? (a,b) and 0 f â' (x 0) = 0 are 2timesderivabile in x
It comes defined one function u(x): = f(x) - f(x0) - f â(x0)(x - x0), for it have u' (x0) = 0 u' (x) = f â(x) and f ' (x) = 0 in how much from the side of x0 where f it is convex has u(x) ³ 0 while from the other side where f it is concave it has u(x) £ 0. Of the rest for 94) also u' ' (x0) = 0 in how much u(x) it does not have a local end in x0 and n he is equal, of rest u' ' (x0) = f ' ' (x0) therefore f â' (x0) = 0.
Error in the approximation with the polynomial of Taylor
37) If f it is a derivabile function n times
in [ a,b ], n 1 times derivabile in [ to, b]/{0} and the derivative n-esima are continuous in
[ a,b ] every for x?[ a,b ] x¹x0 , exists
one q ?(0.1):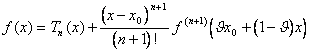 
In order to demonstrate the theorem they come defined 2 functions,
u(x): = f(x) - Tn(x) whose derived in x0 until to the order n are 0 while the derivative in x of order n 1 is un 1(x) = f (n 1)(x)
v(x): = (x-x0)n 1 whose derived in x0 until to the order n are 0 while the derivative in x of order n 1 is vn 1(x) = (n 1)!
Having to reach the result that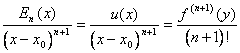 
we ricorsivamente apply the theorem of Cauchy until reaching the order
derivative n 1 taking advantage of in every passage that the
derivatives until to the degree n are null in x0 , in particular, applying a 1ª turns
the theorem of Cauchy identifies a point y1 in which the relationship between the two
functions is equal to the relationship between the 2 derivatives
first. Applying a 2ª it turns this theorem to interval (x0 , y1) determines a point y2 in which the relationship of the
second derivatives is equal to the relationship of the functions.
Proceeding ulteriorly, to the step n 1 a point y n 1 is characterized in which
exposed how much from the theorem is verified that is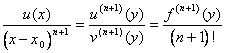 
.